本文主要是介绍文本分类之降维技术之特征抽取之LDA线性判别分析,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
背景:为什么需要特征抽取?
基于的向量空间模型有个缺点,即向量空间中的每个关键词唯一地代表一个概念或语义单词,也就是说它不能处理同义词和多义词,然而实际情况是:一个词往往有多个不同的含义,多个不同的词可以代表一个概念。在这种情况下,基于的向量空间模型不能很好的解决这种问题。
特征抽取方法则可以看作从测量空间到特征空间的一种映射或变换,一般是通过构造一个特征评分函数,把测量空间的数据投影到特征空间,得到在特征空间的值,然后根据特征空间中的值抽取最高的若干个特征。
常用的特征抽取方法主要有线性判别分析(LDA)、主成分分析(PCA)、潜在语义索引(LSI)、非负矩阵分解,因子分析,单词聚类,规则提取等。
1、LDA(线性判别分析) 既可以用于降维,也可以用于多文本的多分类。
LDA是有监督的方式,它先对训练数据进行降维,然后找出一个线性判别函数。
LDA的全称是Linear Discriminant Analysis(线性判别分析),是一种supervised learning。有些资料上也称为是Fisher’s Linear Discriminant,因为它被Ronald Fisher发明自1936年,Discriminant这次词我个人的理解是,一个模型,不需要去通过概率的方法来训练、预测数据,比如说各种贝叶斯方法,就需要获取数据的先验、后验概率等等。LDA是在目前机器学习、数据挖掘领域经典且热门的一个算法,据我所知,百度的商务搜索部里面就用了不少这方面的算法。
LDA的原理是,将带上标签的数据(点),通过投影的方法,投影到维度更低的空间中,使得投影后的点,会形成按类别区分,一簇一簇的情况,相同类别的点,将会在投影后的空间中更接近。要说明白LDA,首先得弄明白线性分类器:因为LDA是一种线性分类器。对于K-分类的一个分类问题,会有K个线性函数:
![]()
当满足条件:对于所有的j,都有Yk > Yj,的时候,我们就说x属于类别k。对于每一个分类,都有一个公式去算一个分值,在所有的公式得到的分值中,找一个最大的,就是所属的分类了。
上式实际上就是一种投影,是将一个高维的点投影到一条高维的直线上,LDA最求的目标是,给出一个标注了类别的数据集,投影到了一条直线之后,能够使得点尽量的按类别区分开,当k=2即二分类问题的时候,如下图所示:
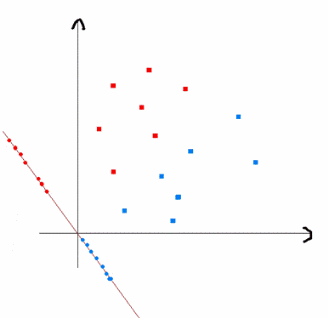
红色的方形的点为0类的原始点、蓝色的方形点为1类的原始点,经过原点的那条线就是投影的直线,从图上可以清楚的看到,红色的点和蓝色的点被原点明显的分开了,这个数据只是随便画的,如果在高维的情况下,看起来会更好一点。下面我来推导一下二分类LDA问题的公式:
假设用来区分二分类的直线(投影函数)为:
![]()
LDA分类的一个目标是使得不同类别之间的距离越远越好,同一类别之中的距离越近越好,所以我们需要定义几个关键的值。
类别i的原始中心点为:(Di表示属于类别i的点)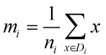
类别i投影后的中心点为:
![]()
衡量类别i投影后,类别点之间的分散程度(方差)为:
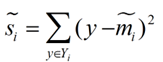
最终我们可以得到一个下面的公式,表示LDA投影到w后的损失函数:
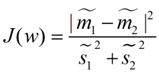
我们分类的目标是,使得类别内的点距离越近越好(集中),类别间的点越远越好。分母表示每一个类别内的方差之和,方差越大表示一个类别内的点越分散,分子为两个类别各自的中心点的距离的平方,我们最大化J(w)就可以求出最优的w了。想要求出最优的w,可以使用拉格朗日乘子法,但是现在我们得到的J(w)里面,w是不能被单独提出来的,我们就得想办法将w单独提出来。
我们定义一个投影前的各类别分散程度的矩阵,这个矩阵看起来有一点麻烦,其实意思是,如果某一个分类的输入点集Di里面的点距离这个分类的中心店mi越近,则Si里面元素的值就越小,如果分类的点都紧紧地围绕着mi,则Si里面的元素值越更接近0.
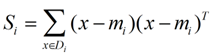
带入Si,将J(w)分母化为:
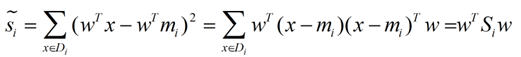
![]()
同样的将J(w)分子化为:
![]()
这样损失函数可以化成下面的形式:
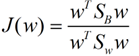
这样就可以用最喜欢的拉格朗日乘子法了,但是还有一个问题,如果分子、分母是都可以取任意值的,那就会使得有无穷解,我们将分母限制为长度为1(这是用拉格朗日乘子法一个很重要的技巧,在下面将说的PCA里面也会用到,如果忘记了,请复习一下高数),并作为拉格朗日乘子法的限制条件,带入得到:
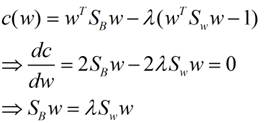
这样的式子就是一个求特征值的问题了。
对于N(N>2)分类的问题,我就直接写出下面的结论了:
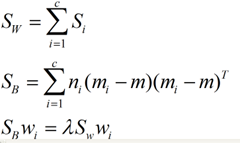
这同样是一个求特征值的问题,我们求出的第i大的特征向量,就是对应的Wi了。
这里想多谈谈特征值,特征值在纯数学、量子力学、固体力学、计算机等等领域都有广泛的应用,特征值表示的是矩阵的性质,当我们取到矩阵的前N个最大的特征值的时候,我们可以说提取到的矩阵主要的成分。在机器学习领域,不少的地方都要用到特征值的计算,比如说图像识别、pagerank、LDA、PCA等等。
以下是一个LDA的例子:
下面我们利用LDA进行一个分类的问题:假设一个产品有两个参数来衡量它是否合格,
我们假设两个参数分别为:
| 参数A | 参数B | 是否合格 |
| 2.95 | 6.63 | 合格 |
| 2.53 | 7.79 | 合格 |
| 3.57 | 5.65 | 合格 |
| 3.16 | 5.47 | 合格 |
| 2.58 | 4.46 | 不合格 |
| 2.16 | 6.22 | 不合格 |
| 3.27 | 3.52 | 不合格 |
实验数据来源:http://people.revoledu.com/kardi/tutorial/LDA/Numerical Example.html
所以我们可以根据上图表格把样本分为两类,一类是合格的,一类是不合格的,所以我们可以创建两个数据集类:
cls1_data
3.1600
cls2_data
其中cls1_data为合格样本,cls2_data为不合格的样本,我们根据公式(1),(2)可以算出合格的样本的期望值,不合格类样本的合格的值,以及总样本期望:
E_cls1
3.0525
E_cls2
2.6700
E_all
2.8886
我们可以做出现在各个样本点的位置:
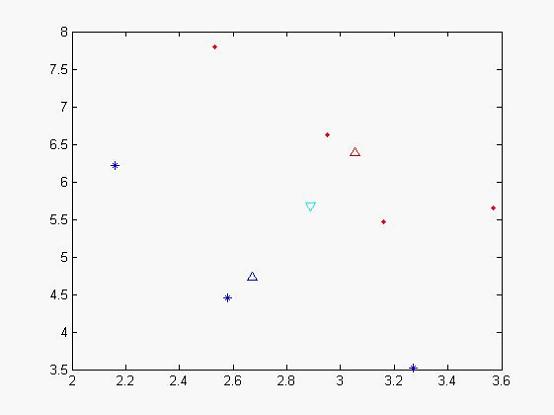
图一
其中蓝色‘*’的点代表不合格的样本,而红色实点代表合格的样本,天蓝色的倒三角是代表总期望,蓝色三角形代表不合格样本的期望,红色三角形代表合格样本的期望。从x,y轴的坐标方向上可以看出,合格和不合格样本区分度不佳。
我们在可以根据表达式(3),(4)可以计算出类间离散度矩阵和类内离散度矩阵:
Sb
0.1547
Sw
我们可以根据公式(7),(8)算出![]() 特征值以及对应的特征向量:
特征值以及对应的特征向量:
L
对角线上为特征值,第一个特征值太小被计算机约为0了
与他对应的特征向量为
V
0.2256
根据取最大特征值对应的特征向量:(-0.9230,-0.3848),该向量即为我们要求的子空间,我们可以把原来样本投影到该向量后
new_cls1_data
为合格样本投影后的样本值
new_cls2_data
为不合格样本投影后的样本值,我们发现投影后,分类效果比较明显,类和类之间聚合度很高,我们再次作图以便更直观看分类效果
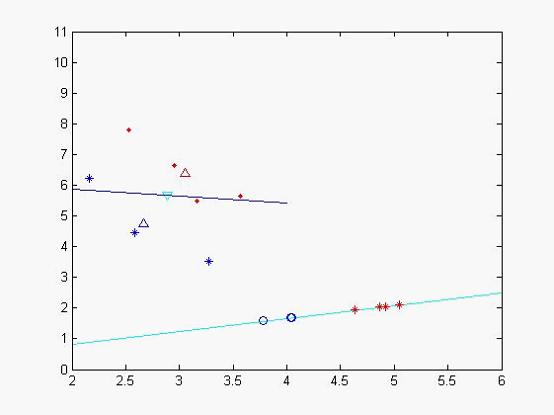
图二
蓝色的线为特征值较小所对应的特征向量,天蓝色的为特征值较大的特征向量,其中蓝色的圈点为不合格样本在该特征向量投影下来的位置,二红色的‘*’符号的合格样本投影后的数据集,从中个可以看出分类效果比较好(当然由于x,y轴单位的问题投影不那么直观)。
我们再利用所得到的特征向量,来对其他样本进行判断看看它所属的类型,我们取样本点
(2.81,5.46),
我们把它投影到特征向量后得到:result
这篇关于文本分类之降维技术之特征抽取之LDA线性判别分析的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




