本文主要是介绍粒子群算法PSO优化BP神经网络预测MATLAB代码实现(PSO-BP预测),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
本文以MATLAB自带的脂肪数据集为例,数据集为EXCEL格式,接下来介绍粒子群算法优化BP神经网络预测的MATLAB代码步骤,主要流程包括1. 读取数据 2.划分训练集和测试集 3.归一化 4.确定BP神经网络的隐含层最优节点数量 5. 使用粒子群算法优化BP的神经网络权重和阈值 6. 利用优化后的参数训练BP神经网络 7. 计算BP和PSO-BP的测试集预测误差,包括MAE、RMSE、MAPE、拟合优度R方,以及作优化前后的预测值和真实值对比图。
一般来说通过加入启发式算法以及调试好参数后,模型的预测性能将具有明显的提升。下图是优化结果,相对误差从28%降低到7%,粒子群算法的优化效果非常明显。

以下是粒子群算法PSO优化BP预测代码:
1. 初始化代码
clear % 清除工作区,防止工作区存在相关变量对代码产生影响
close all % 关闭所有已有图像
clc % 清空命令行窗口
2. 读取数据代码
data=xlsread('数据.xlsx','Sheet1','A1:N252'); %%使用xlsread函数读取EXCEL中对应范围的数据即可
%输入输出数据
input=data(:,1:end-1); %data的第一列-倒数第二列为特征指标
output=data(:,end); %data的最后面一列为输出的指标值
如果从博客直接复制代码,因为没有EXCEL文件,可用以下三行代码替换上面data,input,output三个变量的赋值命令:
% 生成加法器数据集
input = rand(252, 13); % 13个加数作为输入,共252组加法题
output = sum(input, 2); % 13个加数之和作为输出
data = [input, output]; % 合并输入与输出数据集3. 划分训练集、测试集代码
N=length(output); %全部样本数目
testNum=15; %设定测试样本数目
trainNum=N-testNum; %计算训练样本数目input_train = input(1:trainNum,:)';
output_train =output(1:trainNum)';
input_test =input(trainNum+1:trainNum+testNum,:)';
output_test =output(trainNum+1:trainNum+testNum)';
4. 数据归一化代码
[inputn,inputps]=mapminmax(input_train,0,1);
[outputn,outputps]=mapminmax(output_train);
inputn_test=mapminmax('apply',input_test,inputps);
5. 确定隐含层节点个数代码
inputnum=size(input,2);
outputnum=size(output,2);
disp('/')
disp('神经网络结构...')
disp(['输入层的节点数为:',num2str(inputnum)])
disp(['输出层的节点数为:',num2str(outputnum)])
disp(' ')
disp('隐含层节点的确定过程...')%确定隐含层节点个数
%采用经验公式hiddennum=sqrt(m+n)+a,m为输入层节点个数,n为输出层节点个数,a一般取为1-10之间的整数
MSE=1e+5; %初始化最小误差
for hiddennum=fix(sqrt(inputnum+outputnum))+1:fix(sqrt(inputnum+outputnum))+10%构建网络net=newff(inputn,outputn,hiddennum);% 网络参数net.trainParam.epochs=1000; % 训练次数net.trainParam.lr=0.01; % 学习速率net.trainParam.goal=0.000001; % 训练目标最小误差% 网络训练net=train(net,inputn,outputn);an0=sim(net,inputn); %仿真结果mse0=mse(outputn,an0); %仿真的均方误差disp(['隐含层节点数为',num2str(hiddennum),'时,训练集的均方误差为:',num2str(mse0)])%更新最佳的隐含层节点if mse0<MSEMSE=mse0;hiddennum_best=hiddennum;end
end
disp(['最佳的隐含层节点数为:',num2str(hiddennum_best),',相应的均方误差为:',num2str(MSE)])
以下是运行代码后在命令行窗口打印的神经网络结构
/
神经网络结构...
输入层的节点数为:13
输出层的节点数为:1隐含层节点的确定过程...
隐含层节点数为4时,训练集的均方误差为:0.031275
隐含层节点数为5时,训练集的均方误差为:0.034734
隐含层节点数为6时,训练集的均方误差为:0.035053
隐含层节点数为7时,训练集的均方误差为:0.027684
隐含层节点数为8时,训练集的均方误差为:0.030898
隐含层节点数为9时,训练集的均方误差为:0.031399
隐含层节点数为10时,训练集的均方误差为:0.027933
隐含层节点数为11时,训练集的均方误差为:0.029294
隐含层节点数为12时,训练集的均方误差为:0.046231
隐含层节点数为13时,训练集的均方误差为:0.031752
最佳的隐含层节点数为:7,相应的均方误差为:0.027684
6. 构建最佳隐含层节点的BP神经网络代码
disp(' ')
disp('标准的BP神经网络:')
net0=newff(inputn,outputn,hiddennum_best,{'tansig','purelin'},'trainlm');% 建立模型%网络参数配置
net0.trainParam.epochs=1000; % 训练次数,这里设置为1000次
net0.trainParam.lr=0.01; % 学习速率,这里设置为0.01
net0.trainParam.goal=0.00001; % 训练目标最小误差,这里设置为0.0001
net0.trainParam.show=25; % 显示频率,这里设置为每训练25次显示一次
net0.trainParam.mc=0.01; % 动量因子
net0.trainParam.min_grad=1e-6; % 最小性能梯度
net0.trainParam.max_fail=6; % 最高失败次数%开始训练
net0=train(net0,inputn,outputn);%预测
an0=sim(net0,inputn_test); %用训练好的模型进行仿真%预测结果反归一化与误差计算
test_simu0=mapminmax('reverse',an0,outputps); %把仿真得到的数据还原为原始的数量级%误差指标
[mae0,mse0,rmse0,mape0,error0,errorPercent0]=calc_error(output_test,test_simu0);以下是对BP神经网络预测结果的性能评估
标准的BP神经网络:
平均绝对误差mae为: 4.7787
均方误差mse为: 30.1094
均方误差根rmse为: 5.4872
平均绝对百分比误差mape为: 23.8809 %
7. 粒子群算法寻最优权值阈值代码
disp(' ')
disp('PSO优化BP神经网络:')
net=newff(inputn,outputn,hiddennum_best,{'tansig','purelin'},'trainlm');% 建立模型%网络参数配置
net.trainParam.epochs=1000; % 训练次数,这里设置为1000次
net.trainParam.lr=0.01; % 学习速率,这里设置为0.01
net.trainParam.goal=0.00001; % 训练目标最小误差,这里设置为0.0001
net.trainParam.show=25; % 显示频率,这里设置为每训练25次显示一次
net.trainParam.mc=0.01; % 动量因子
net.trainParam.min_grad=1e-6; % 最小性能梯度
net.trainParam.max_fail=6; % 最高失败次数%初始化PSO参数
popsize=10; %初始种群规模
maxgen=50; %最大进化代数
dim=inputnum*hiddennum_best+hiddennum_best+hiddennum_best*outputnum+outputnum; %自变量个数
lb=repmat(-3,1,dim); %自变量下限
ub=repmat(3,1,dim); %自变量上限
c1 = 2; % 每个粒子的个体学习因子,也称为个体加速常数
c2 = 2; % 每个粒子的社会学习因子,也称为社会加速常数
w = 0.9; % 惯性权重
vmax =3*ones(1,dim); % 粒子的最大速度
vmax=repmat(vmax,popsize,1);
x = zeros(popsize,dim);
for i = 1: dimx(:,i) = lb(i) + (ub(i)-lb(i))*rand(popsize,1); % 随机初始化粒子所在的位置在定义域内
end
v = -vmax + 2*vmax .* rand(popsize,dim); % 随机初始化粒子的速度(设置为[-vmax,vmax])
8. 计算适应度代码
fit = zeros(popsize,1); % 初始化这n个粒子的适应度全为0
for i = 1:popsize % 循环整个粒子群,计算每一个粒子的适应度fit(i) = fitness(x(i,:),inputnum,hiddennum_best,outputnum,net,inputn,outputn,output_train,inputn_test,outputps,output_test); % 调用函数来计算适应度
end
pbest = x; % 初始化这n个粒子迄今为止找到的最佳位置
ind = find(fit == min(fit), 1); % 找到适应度最小的那个粒子的下标
gbest = x(ind,:); % 定义所有粒子迄今为止找到的最佳位置
9. 迭代寻优代码
Convergence_curve = ones(maxgen,1); % 初始化每次迭代得到的最佳的适应度
h0 = waitbar(0,'进度','Name','PSO optimization...',...'CreateCancelBtn','setappdata(gcbf,''canceling'',1)');
setappdata(h0,'canceling',0);for d = 1:maxgen % 开始迭代,一共迭代K次for i = 1:popsize % 依次更新第i个粒子的速度与位置v(i,:) = w*v(i,:) + c1*rand(1)*(pbest(i,:) - x(i,:)) + c2*rand(1)*(gbest - x(i,:)); % 更新第i个粒子的速度% 如果粒子的速度超过了最大速度限制,就对其进行调整for j = 1: dimif v(i,j) < -vmax(j)v(i,j) = -vmax(j);elseif v(i,j) > vmax(j)v(i,j) = vmax(j);endendx(i,:) = x(i,:) + v(i,:); % 更新第i个粒子的位置% 如果粒子的位置超出了定义域,就对其进行调整for j = 1: dimif x(i,j) < lb(j)x(i,j) = lb(j);elseif x(i,j) > ub(j)x(i,j) = ub(j);endend%更新第i个粒子的适应度fit(i) = fitness(x(i,:),inputnum,hiddennum_best,outputnum,net,inputn,outputn,output_train,inputn_test,outputps,output_test);%更新当前最优粒子位置if fit(i) < fitness(pbest(i,:),inputnum,hiddennum_best,outputnum,net,inputn,outputn,output_train,inputn_test,outputps,output_test) % 如果第i个粒子的适应度小于这个粒子迄今为止找到的最佳位置对应的适应度pbest(i,:) = x(i,:); % 那就更新第i个粒子迄今为止找到的最佳位置end%更新历史最优粒子位置if fitness(pbest(i,:),inputnum,hiddennum_best,outputnum,net,inputn,outputn,output_train,inputn_test,outputps,output_test) < fitness(gbest,inputnum,hiddennum_best,outputnum,net,inputn,outputn,output_train,inputn_test,outputps,output_test) % 如果第i个粒子的适应度小于所有的粒子迄今为止找到的最佳位置对应的适应度gbest = pbest(i,:); % 那就更新所有粒子迄今为止找到的最佳位置endendConvergence_curve(d) = fitness(gbest,inputnum,hiddennum_best,outputnum,net,inputn,outputn,output_train,inputn_test,outputps,output_test); % 更新第d次迭代得到的最佳的适应度waitbar(d/maxgen,h0,[num2str(d/maxgen*100),'%'])if getappdata(h0,'canceling')breakend
end
delete(h0)
Best_pos =gbest;
Best_score = Convergence_curve(end);
setdemorandstream(pi);
% 绘制进化曲线
figure
plot(Convergence_curve,'r-','linewidth',2)
xlabel('进化代数')
ylabel('均方误差')
legend('最佳适应度')
title('PSO的进化收敛曲线')
w1=Best_pos(1:inputnum*hiddennum_best); %输入层到中间层的权值
B1=Best_pos(inputnum*hiddennum_best+1:inputnum*hiddennum_best+hiddennum_best); %中间各层神经元阈值
w2=Best_pos(inputnum*hiddennum_best+hiddennum_best+1:inputnum*hiddennum_best+hiddennum_best+hiddennum_best*outputnum); %中间层到输出层的权值
B2=Best_pos(inputnum*hiddennum_best+hiddennum_best+hiddennum_best*outputnum+1:inputnum*hiddennum_best+hiddennum_best+hiddennum_best*outputnum+outputnum); %输出层各神经元阈值
%矩阵重构
net.iw{1,1}=reshape(w1,hiddennum_best,inputnum);
net.lw{2,1}=reshape(w2,outputnum,hiddennum_best);
net.b{1}=reshape(B1,hiddennum_best,1);
net.b{2}=reshape(B2,outputnum,1);
10. 优化后的神经网络训练代码
net=train(net,inputn,outputn);%开始训练,其中inputn,outputn分别为输入输出样本
11. 优化后的神经网络测试代码
an1=sim(net,inputn_test);
test_simu1=mapminmax('reverse',an1,outputps); %把仿真得到的数据还原为原始的数量级
%误差指标
[mae1,mse1,rmse1,mape1,error1,errorPercent1]=calc_error(output_test,test_simu1);
以下是对优化后的BP神经网络预测结果的性能评估,相对误差从28%降低到7%,粒子群算法的优化效果非常明显。
平均绝对误差mae为: 1.5899
均方误差mse为: 3.343
均方误差根rmse为: 1.8284
平均绝对百分比误差mape为: 7.0475 %
12. BP预测结果和PSO-BP预测结果对比作图代码
figure
plot(output_test,'b-*','linewidth',1)
hold on
plot(test_simu0,'r-v','linewidth',1,'markerfacecolor','r')
hold on
plot(test_simu1,'k-o','linewidth',1,'markerfacecolor','k')
legend('真实值','BP预测值','PSO-BP预测值')
xlabel('测试样本编号')
ylabel('指标值')
title('PSO优化前后的BP神经网络预测值和真实值对比图')figure
plot(error0,'rv-','markerfacecolor','r')
hold on
plot(error1,'ko-','markerfacecolor','k')
legend('BP预测误差','PSO-BP预测误差')
xlabel('测试样本编号')
ylabel('预测偏差')
title('PSO优化前后的BP神经网络预测值和真实值误差对比图')disp(' ')
disp('/')
disp('打印结果表格')
disp('样本序号 实测值 BP预测值 PSO-BP值 BP误差 PSO-BP误差')
for i=1:testNumdisp([i output_test(i),test_simu0(i),test_simu1(i),error0(i),error1(i)])
end
下图是运行后粒子群算法的适应度曲线,也叫进化曲线。从图中可以看出随着迭代次数的增加,神经网络预测误差在不断下降,约47代达到终值。
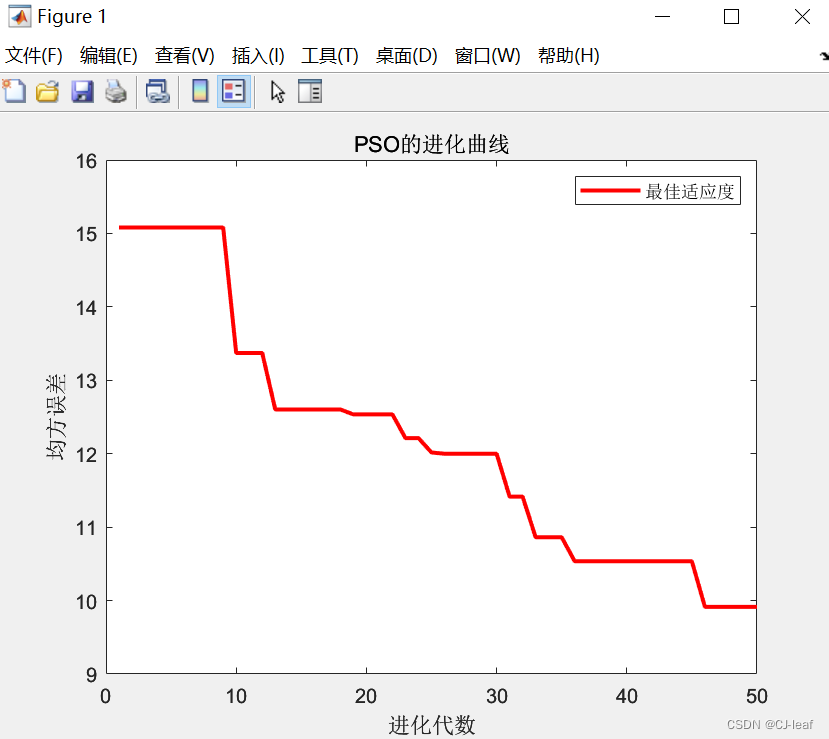
PSO-BP和BP预测结果对比图如下,图中带星号蓝线表示真实值,红线表示BP预测结果,黑线表示PSO优化后的BP预测结果,可以看到黑线和蓝线最为接近,也说明PSO对BP预测结果起到了优化作用。
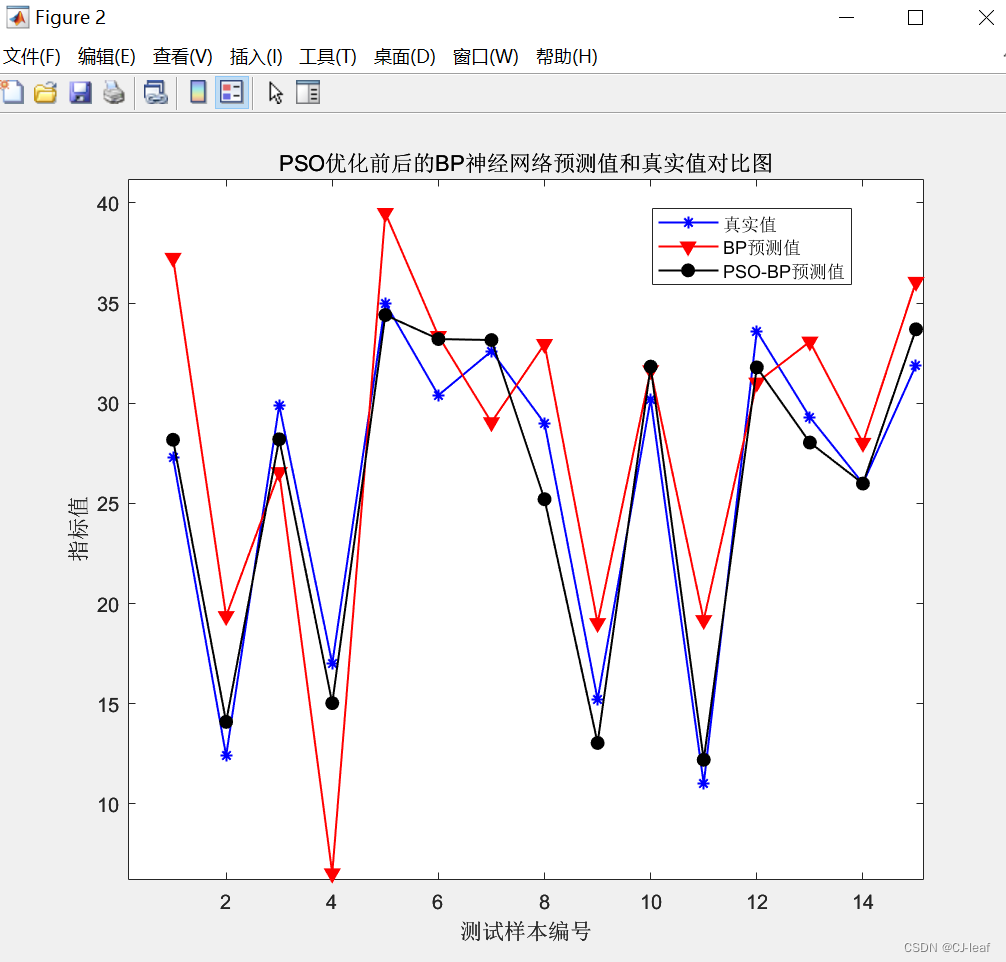
分别对PSO-BP和BP的预测结果与真实值做误差,误差计算的结果见下图,可以看到PSO-BP误差稳定在±3内,而BP预测误差在±10内,也可说明PSO-BP的优化效果明显。
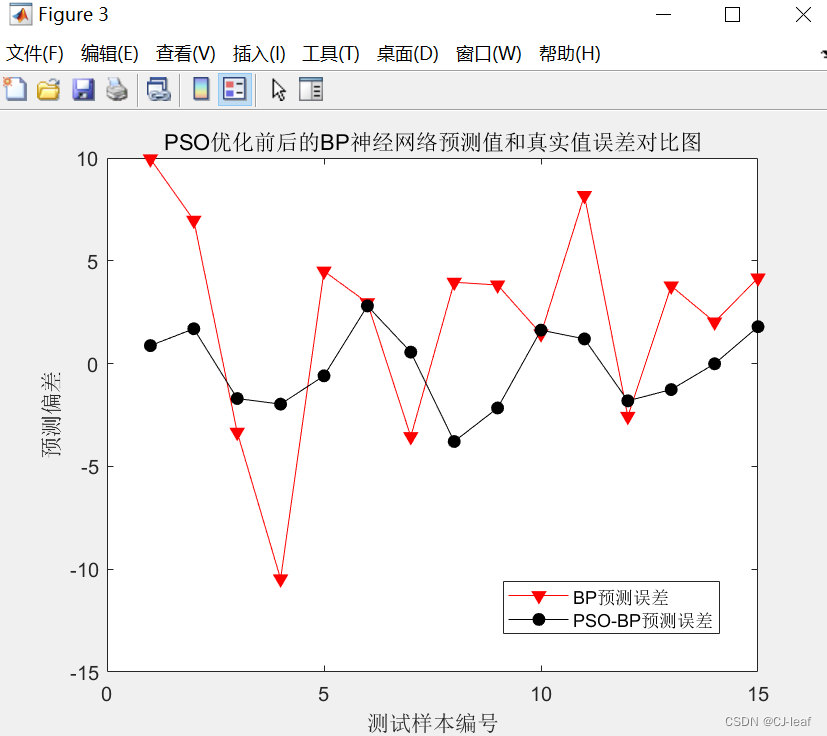
以上便是粒子群算法优化BP神经网络的代码解读,以及结果分析。如果遇到问题,请直接在评论区留言或者在CSDN私信交流
这篇关于粒子群算法PSO优化BP神经网络预测MATLAB代码实现(PSO-BP预测)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







