本文主要是介绍TSP:常春藤算法IVY求解旅行商问题TSP(可以更改数据),MATLAB代码,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、旅行商问题介绍

二、常春藤算法IVY求解TSP
2.1算法介绍
常春藤算法(Ivy algorithm,IVY)是Mojtaba Ghasemi 等人于2024年提出智能优化算法。该算法模拟了常春藤植物的生长模式,通过协调有序的种群增长以及常春藤植物的扩散和演化来实现。常春藤植物的生长速率是通过微分方程和数据密集型实验过程建模的。该算法利用附近常春藤植物的知识来确定生长方向,并通过选择最近和最重要的邻居进行自我改进。常春藤算法通过保持种群多样性、简单灵活的特点,可以轻松修改和扩展,使研究者和实践者能够探索各种修改和技术以增强其性能和能力。
参考文献:
[1]Mojtaba Ghasemi, Mohsen Zare, Pavel Trojovský, Ravipudi Venkata Rao, Eva Trojovská, Venkatachalam Kandasamy,Optimization based on the smart behavior of plants with its engineering applications: Ivy algorithm,Knowledge-Based Systems,Volume 295,2024.https://doi.org/10.1016/j.knosys.2024.111850.
2.2部分代码
close all
clear
clc
%数据集参考文献 REINELT G.TSPLIB-a traveling salesman problem[J].ORSA Journal on Computing,1991,3(4):267-384.
global data
load('data.txt')%导入TSP数据集bayg29
Dim=size(data,1)-1;%维度
lb=-100;%下界
ub=100;%上界
fobj=@Fun;%计算总距离
SearchAgents_no=100; % 种群大小(可以修改)
Max_iteration=10000; % 最大迭代次数(可以修改)
[fMin,bestX,curve]=(SearchAgents_no,Max_iteration,lb,ub,Dim,fobj);
%% 画最终的结果 Kd是最终的城市序列
[~,idx]=sort(bestX);
idx=idx+1;
Kd(1)=1;
Kd(2:length(idx)+1)=idx;
Kd(length(idx)+2)=1;
%% 画路径图
figure
plot(data(Kd,1),data(Kd,2),'go','MarkerFaceColor','g')
2.3部分结果
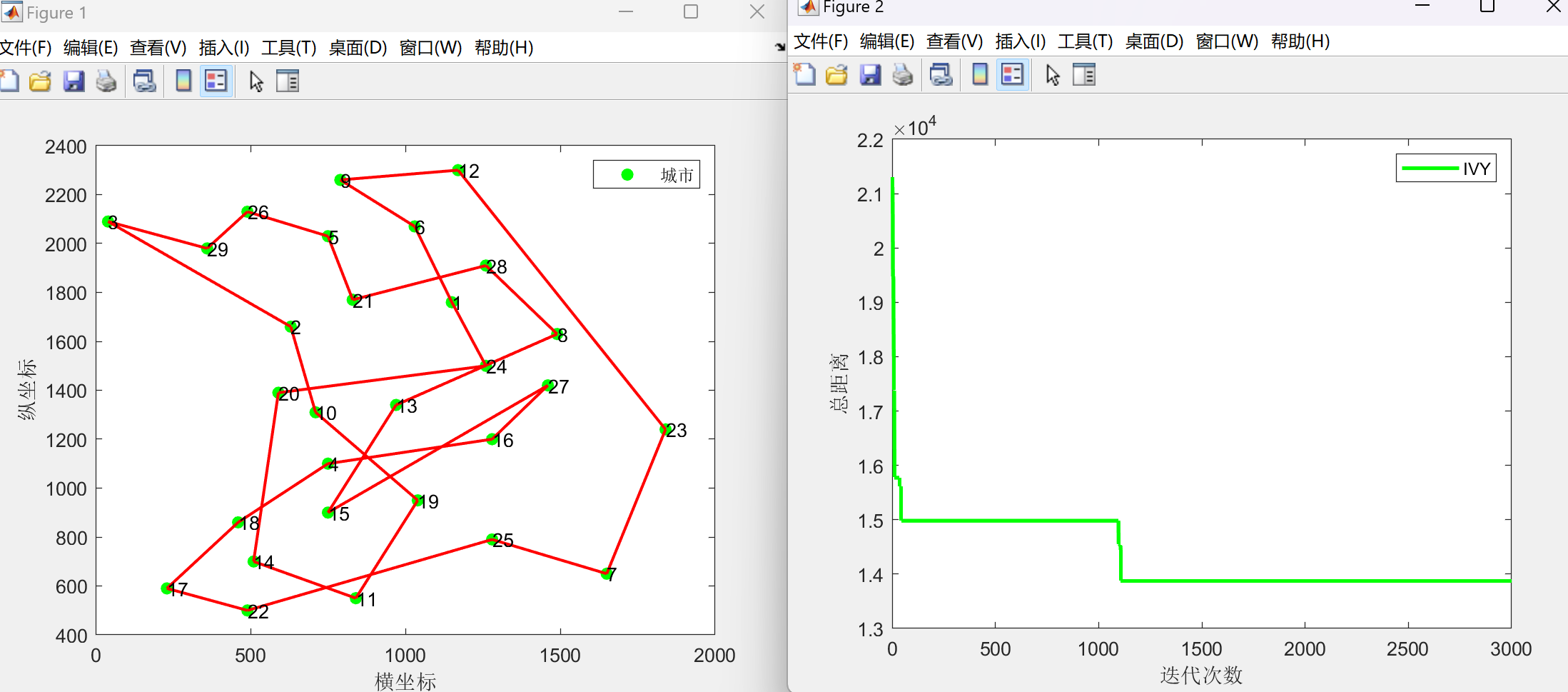
算法得到的路径:1 > 6 > 9 > 12 > 23 > 7 > 25 > 22 > 17 > 18 > 4 > 16 > 27 > 15 > 13 > 8 > 28 > 21 > 5 > 26 > 29 > 3 > 2 > 10 > 19 > 11 > 14 > 20 > 24 > 1
算法求解的总路径总长:13873.9529
三、完整MATLAB代码
TSP:肺功能优化算法LPO求解旅行商问题TSP(可以更改数据),MATLAB代码
TSP:常春藤算法IVY求解旅行商问题TSP(可以更改数据),MATLAB代码
TSP:差异化创意搜索算法DCS求解旅行商问题TSP(可以更改数据),MATLAB代码
TSP:人工原生动物优化器(APO)求解旅行商问题TSP(可以更改数据),MATLAB代码
TSP:黑翅鸢算法BKA求解旅行商问题TSP(可以更改数据),MATLAB代码
这篇关于TSP:常春藤算法IVY求解旅行商问题TSP(可以更改数据),MATLAB代码的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









