本文主要是介绍数学建模----单源最短路径模型建立和求解,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
1.引言和声明
2.单源最短路径
3.建立模型
4.代码求解
1.引言和声明
(1)最近又在准备学习matlab,有了一些新的理解和体会,记录一下;
(2)这个首先要声明两个符号,这两个符号也是今天才知道两者之间的区别;
就是在Matlab里面,我们经常使用%作为标记,一个百分号就是普通的注释,两个百分号就是表示的对于这个编辑器的文本分割,把这个代码分割成为不同的部分,这个其实是有快捷键的,但是我之前尝试过,不是很好记,我觉得这个输入两个百分号之后,使用这个enter之后就可以自动实现这个区域的划分,还是很方便的;
2.单源最短路径
(1)任意单元最短路径的子路径还是最短路径,这个原理就是迪杰斯特拉算法的贪心算法原理;
(2)单元最短路径的赛题介绍:这个本质上就是单元最短路径,但是实际应用的时候这个不仅仅局限于求这个路径问题,像我们下面展示的这个设备的更新问题,本质上就是进行求解这个单源最短路径,两者的思路和方法是一致的,可能初学者体会不到这一点,但是我们可以慢慢理解;

(3) 这个题干上面的要求就是这个有一台设备,这个设备在年初的时候需要决定是买新的还是维修之后继续使用,目标函数就是五年之后的这个总的费用最小;
买新的设备需要支付钱,但是维修旧的设备也是需要花钱的,而且随着这个设备的使用时间的增加,这个设备的维修成本就会越来越高,这个费用就会越来越多,但是每一年这个购买新的设备的成本是波动不大的,这个时候我们就需要进行考虑支付的费用的问题,这个如何进行这个选择,是维修还是购买新的设备,才可以让这个支付的费用最少;
3.建立模型
(1)要想让这个最小费用的问题和我们前面介绍的这个单源最短路径问题结合起来,这个时候我们就要把这个条件之间相互匹配,如何进行这个匹配,首先就是我们的这个单源最短路径上面有的是这个路径的长度和路径的权重,我们在计算这个问题的时候,就是用这个权重,这个模型里面的最短路径肯定就是我们求解时候的这个最小的支付费用,这个是毋庸置疑的;
(2)但是这个设备的维修以及这个重新购买如何与这个模型里面的已知的直观量建立联系,这个是我们遇到的比较棘手的问题;
我们把这个实际问题抽象成一个数学问题,使用这个图表示这个关系,如下图所示:
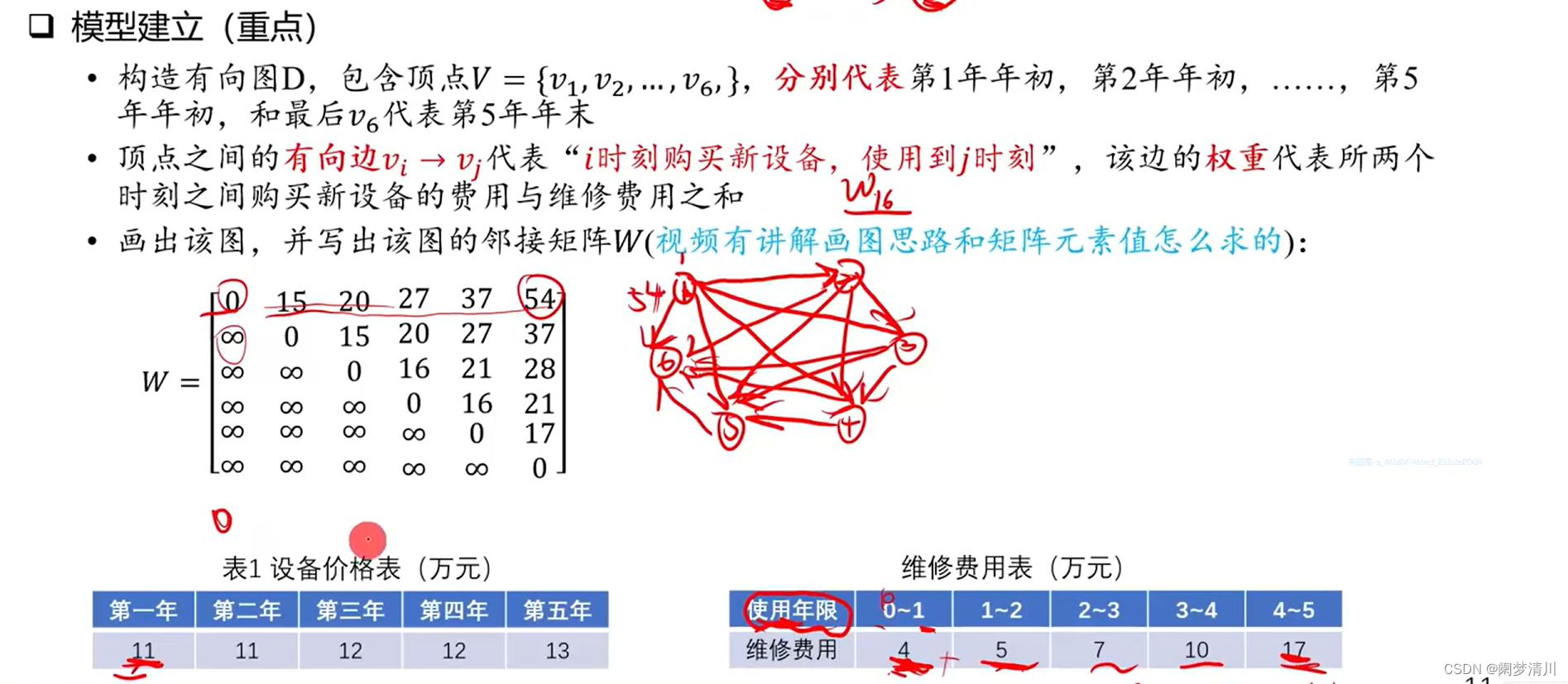
(3)这个图里面的顶点就代表着年,这里一共是6个顶点,分别代表着第一年年初,第二年年初,第三年年初,第四年年初,第五年年初,第五年年末,一条边链接两个顶点,这个意义就是其实顶点年份买,终止顶点结束使用(就是一直用到这个时间停止),这个我们在第五年的时候也在使用,因此我们设置了第六个顶点代表我们的第五年年末,如果只有5个顶点的话,这个第五年的使用没有办法显示,因此我们设计了六个顶点;
(4)这个邻接矩阵也需要我们仔细的理解,为什么主对角线下面的元素都是无穷,上面的元素有具体的值,主对角线元素是0,这个就和这个问题的实际意义相关,因为这个我们这个矩阵元素表示的意义就是第i年买进设备,第j年停止使用,我们举一个例子,例如这个矩阵里面的第三行元素,表示我们使第三年买的设备,这一行的第一个元素表示的就是第一年结束使用,这个肯定是不存在的,同理第二个也是不存在的,这个数值表示的就是购买费用和维修费用的和,这两个不存在,我们使用无穷表示 ,自己到自己 就是使用0进行表示的,那么我们第三年购买,就只能使用到第四年,第五年,第六年,所以第三行上面只有这个三个位置元素有具体的数值;
(5)这个数值是怎么进行计算的,
以这个第三行第六个数据为例,这个表示的就是第三年购买,使用到第六年,购买费用加上这个维修费用表示的就是这个位置的数值,这个费用是28,就是第三年购买费用费用12,加上维修费用,使用第一年,也就是第三年(因为是第三年购买的)需要费用4,使用第二年,就是第四年,需要费用5,使用第三年,也就是第六年,维修费用7,这个加起来就是28,同理可以得到其他的这个费用;
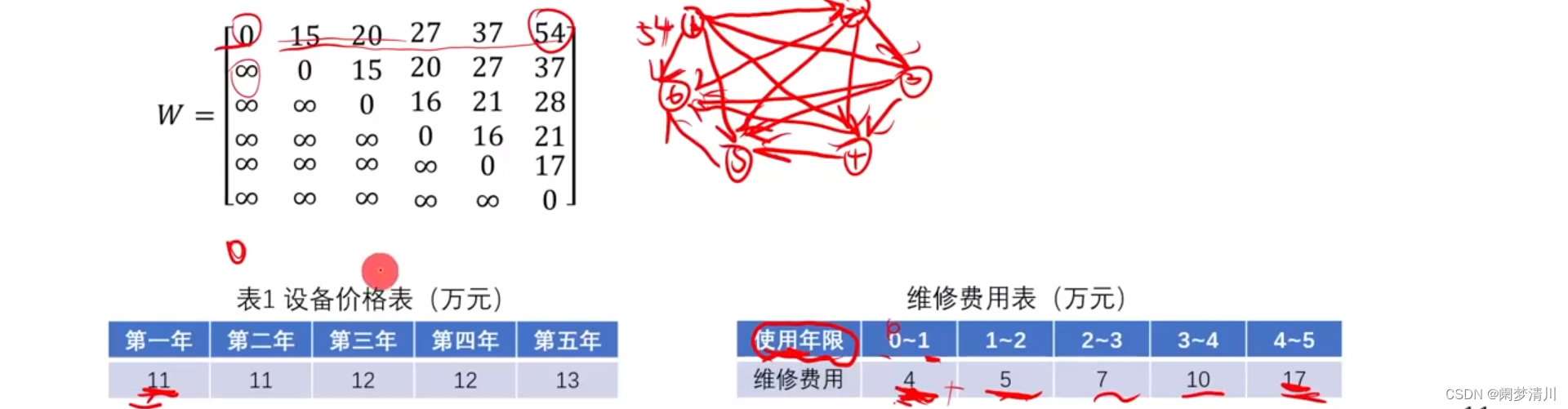
(6)需要注意的就是,在amtalb里面写代码的时候,这个正无穷是使用0进行写进代码的,这个里面我们只是写无穷给读者们看的,我们写0是给这个matlab看的,这个针对不同的对象,我们的这个数字的表现形式也是不一样的;
4.代码求解
(1)这个部分,我们就要使用相关的函数把这个数学语言转化为代码,让这个计算机帮助我们进行这个模型的求解,首先我们肯定是要把这个邻接矩阵表示出来的 ,我们的方法就是
我们上面已经说过,在这个matlab里面,我们把所有的无穷使用0表示,使用无穷反而影响这个matlab的运算;

这个我们现实生成了一个6行6列的邻接矩阵,全部是0,我们再去进行相应的修改,把不是0位置元素修改为指定的数值,这个里面的修改方法简体提一下,这个中括号里面就是一个索引,表示的就是从第几个到第几个的意思;
(2)接下来就是调用函数做出图形
这个18行里面的两个参数也可以写一个,第二个就是为了表示这个顶点(对于顶点的修饰);
cellstr就是把这个顶点的名字放到一个元胞里面去,s可以作为digraph函数的一个参数,digraph函数就是生成一个图论里面的有向图,结果会显示出来;

plot就是作图的指令,里面的参数就是修饰作用,只传递进去一个G也是可以的,感兴趣可以自己查阅后面的其它参数,G就是上面我们的有向图;
highlight就是对于这个图里面的点和线之间突出一下显示而已,这个也是可以复用的,感兴趣可以自行查阅,最后把这个d,path打印出来, d就是这个全部的费用,path就是路径;
(3)问题回答
这个结果表示1 3 6就是路径,说明实际里面就是第一年购买,第三年再换新设备,6表示的就是第五年的年末,就是使用到第五年的年末,这个时候费用最少,为48万元,这个就是这个实际问题的解答,我们需要把这个代码计算结果转换为我们这个题目的已知量信息表示说明;

(4)matlab代码
感兴趣可以自测:
a=zeros(6);
a(1,[2:6])=[15 20 27 37 54];
a(2,[3:6])=[15 20 27 37];
a(3,[4:6])=[16 21 28];
a(4,[5:6])=[16 21];
a(5,6)=17%给每个顶点设置名称,放到这个元胞s里面去;%int2str函数表示的就是把这个数字转换为字符;
% 这个函数我们会使用,也存在这个str2int函数,作用相反%strcat函数就是把这个字符串水平的串联起来s=cellstr(strcat('顶点',int2str([1:6]')));%这个代码就是让这个顶点和1~6数字串联起来%这里进行转置,不转置v1 2 3 4 5 6这个效果G=digraph(a,s);%调用函数生成有向图,第一个参数是矩阵,就是边的权重,第二个参数就是顶点p=plot(G,'layout','force','EdgeColor','k','NodeFontSize',12);[path,d]=shortestpath(G,1,6);highlight(p,path,"EdgeColor","red","LineWidth",2.5);d,path
这篇关于数学建模----单源最短路径模型建立和求解的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




