【论文阅读】-- 时态合并树状图：时态标量数据的基于拓扑的静态可视化

本文主要是介绍【论文阅读】-- 时态合并树状图：时态标量数据的基于拓扑的静态可视化，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

---

期刊: IEEE Trans. Vis. Comput. Graph.（发表日期: 2023）
作者: Wiebke Köpp; Tino Weinkauf

摘要

为时间相关标量场创建一个静态可视化是一个非常复杂的任务，但非常有洞察力，因为它能够在一张图片中展示动态过程。现有的方法基于对领域进行线性化或特征跟踪。领域线性化使用填充空间曲线将所有采样点放置在一个一维域中，从而破坏了个体特征。特征跟踪方法在空间和时间上显式保持特征的连续性，但通常忽略了这些特征所处的数据上下文。我们提出了一种基于特征的空间域线性化方法，通过涉及所有数据样本，将特征保持在一起并保留它们的上下文。我们使用增强的合并树将领域进行线性化，并展示我们的线性化函数具有与原始数据相同的合并树。贪婪优化方案通过时间上的树对齐提供了时间连续性。这导致了一个静态的二维可视化，其中一个维度表示时间，而所有空间维度被压缩到一个维度中。我们将我们的方法与其他领域线性化方法和特征跟踪方法进行了比较，并将其应用于多个真实数据集。

关键词
标量场可视化，增强合并树，基于像素的可视化

1 引言

所有的自然现象本质上都是时间依赖的。这包括天气、气候、流体流动、生物过程、化学反应等。理解这些现象的动力学是数据分析中的一个共同目标。

时变数据可以动态或静态地查看。动态可视化使用动态的图像序列，以瞬态的方式传达数据的动态。这类动画在数据可视化中很常见，并且易于理解，因为数据的动态性与动画可视化的动态性相匹配。然而，动画不能在所有场景中使用(例如,印刷在纸张上)，它的瞬时性使其难以感知某些方面：快速的波动容易被遗漏，移动对象难以计数，甚至来自动画不同部分的动态也难以比较。

动态数据的静态可视化可以同时显示所有的时间步，或者将它们叠加在一起，或者给时间赋予一个空间维度。根据数据的不同，这可能导致一次显示的信息过多，并且占用原本可用于其他可视化元素的空间。尽管如此，它们是动态可视化的一个很好的补充，因为它们往往能够弥补动画的上述问题。

时间相关标量场的静态可视化方法主要分为两类：区域线性化方法和特征追踪方法。将一个域线性化是指将原始2D / 3D数据的所有样本点排列在一个1D域中。然后，时间维度可以正交放置。以前的工作使用空间填充曲线[ 11 ]来实现。不幸的是，空间填充曲线没有保持特征的完整性，这使得某些分析任务无法进行，例如统计特征的数量。

随着时间的推移，特征跟踪方法跟踪不同的感兴趣对象，并创建特征路径/曲面[ 37、38 ]或跟踪图[ 22、31、45 ]，从而可以很容易地用于静态可视化。这些方法自然地保持了特征的完整性，但丢失了数据的更一般方面的信息，如数据的分布情况，即丢失了这些特征所处的数据环境。这是因为( i )特征中不包含的数据样本被排除在进一步处理之外，( ii )特征中的数据样本被汇总到几个统计矩中。

我们提出了一种基于特征的域线性化方法。它通过在一维域中排列所有数据样本来保持特征完整，同时保留其数据上下文。我们建立在合并树的基础上，它提供了基于特征的空间域层次分解，我们用它来将原始的 2D/3D 标量场转换为 1D 函数。值得注意的是，我们表明，在非常温和的假设下，原始数据和一维函数在拓扑上是等效的，因为它们具有用于线性化的相同合并树。

我们通过将时间维度与线性化空间域正交放置来创建整个时间相关数据集的静态二维可视化。我们提出了一种优化方案来同步相邻时间步长的线性化，即实现时间一致性，以便用户可以随着时间的推移在视觉上跟踪特征。

我们做出以下贡献：

• 基于特征的域线性化，通过涉及所有数据样本来保持特征完整并保留其上下文（第 3.1 节），
• 离散优化问题的公式，以通过实用的启发式方法解决时间一致性问题。只需很少的计算工作（第 3.2 节），
• 与线性化和基于特征的方法的评估和比较（第 4 节），以及
• 将我们的方法应用于 2D 和 3D 时间相关数据集（第 5 节）。

2 相关工作及背景介绍

2.1 增广合并树

考虑一个标量场$s:{\mathbb{R}}^n\to \mathbb{R}$的次级集合 { x ∈ R n ∣ s ( x ) ≤ α } \{x \in \mathbb{R}^n | s(x) \leq \alpha\} {x∈Rn∣s(x)≤α}，当等值$\alpha$增加时：每个局部最小值产生一个连通分量，这些分量在鞍点处合并，直到只剩下一个分量，该分量最终会在全局最大值处消失。我们可以用join tree数据结构记录这种行为，如图2所示：局部最小值是叶子节点，鞍点是内部父节点，而全局最大值是根节点。我们将这些称为join tree的超级节点，它们通过超边(superarcs)相互连接。超边代表了次级集合的连通分量。所有数据样本都可以被分配给一条超边。大多数数据样本是常规节点，不会导致拓扑变化。如果我们选择在树数据结构中存储这些常规节点，那么我们称之为增强的join tree。

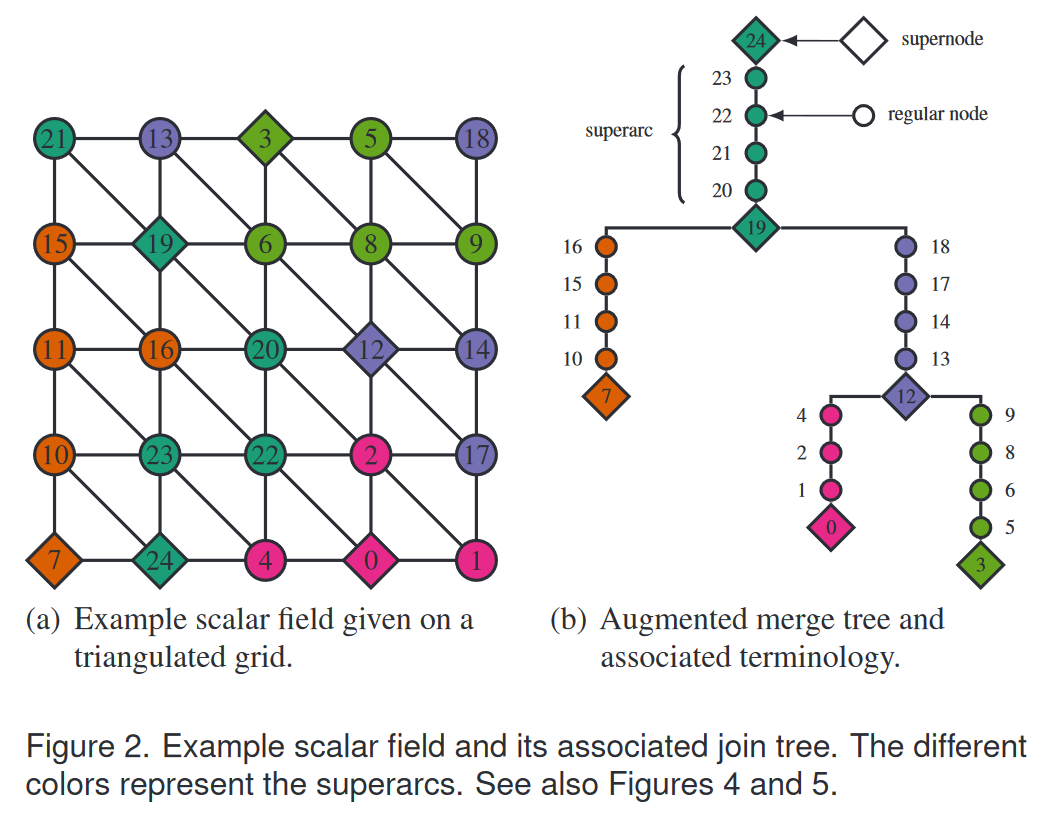
对递减的等值执行此操作可以为我们提供超级别集的分裂树。我们可以将它们都称为合并树。有关更多详细信息，我们参考 Hamish Carr 的优秀博士论文 [6]。图 2 使用一个小标量域示例说明了这些概念，稍后我们将继续使用该标量域来解释图 4 和图 5。在本文的其余部分中，合并树被假定为二叉树。这意味着诸如高原之类的退化情况已经通过诸如简单性模拟之类的策略来处理[10]，并且通过重复对子项分组直到获得二叉树来处理多鞍点。此过程将一些多鞍子节点从常规节点转换为超级节点。图 14 中的 Cylinder 数据集平均每个时间步长有一个多鞍点。

2.2 (增强)合并树的可视化与跟踪

所有树可视化方法也可以应用于合并树。一个常见的例子是树状图[34]，它在拓扑景观中得到应用[43]。合并树是维度之间有趣的中介：它们可以针对任何维度的标量数据进行计算，并且可以在任何维度的空间中可视化。例如，奥斯特林等人。 [24]提出了多维点云的一维拓扑景观剖面，其中每个超弧由一个山状图标表示，该图标由该超弧的大小和持久性参数化。类似的一维拓扑景观剖面也被引入用于优化景观的障碍树 [40, 41] 和密度估计的水平集树 [17]。在特定的参数设置下并应用于标量场，这些产生与我们提出的域线性化等效的结果。

正如 Oesterling 等人所述，随着时间的推移跟踪合并树在计算上是非常昂贵的事情。 [23]。 Lohfink 等人的替代方法。 [19, 20] 和 Pont 等人。 [27]通过采用启发式方法来计算给定相似性度量的树对齐，可以实现更快的计算时间。

我们的方法也使用每个时间步的合并树，但我们使用不同的方法来实现时间一致性：我们将其表示为直接链接原始数据和一维输出数据的离散优化问题。这更直接地满足我们的可视化目的，并且计算速度也非常快。此外，上述方法均未用于创建时间相关数据集的静态二维可视化。

2.3 特征跟踪

存在多种特征跟踪方法来适应不同的特征和数据类型。点或线型要素可以通过求解称为要素流场 [37, 38] 的 ODE 或应用并行向量算子 [2, 26] 来跟踪。这些方法的结果通常叠加在原始域上以实现可视化目的。基于区域的特征（与域具有相同的维度）通常通过重叠[18,21,22,35,45]或统计矩（例如直方图[30]）来跟踪。这些导致跟踪图的平面布局成为研究主题 [18, 22]。基于区域的跟踪方法与我们的工作相关，因为它们经常也考虑子/超级集。然而，上述方法采用固定阈值，而我们的工作使用合并树来描述整个数据范围内子/超级别集的拓扑，没有任何阈值。

基于特征的方法的一个目标是将原始数据附带的信息量大幅减少为一小组特征。因此，特征轨迹的可视化通常是抽象的——例如嵌套跟踪图[22]——除了特征的存在和对应关系之外，只携带很少的数据信息。相比之下，我们的工作旨在在一张图像中显示特征以及整个数据上下文。

2.4 数据线性化

单位线段上的点与n维空间中的点之间存在一一对应关系这一令人震惊的事实是由Georg Cantor首次观察到并证明的[5]。受这一结果的激励，朱塞佩·皮亚诺 (Giuseppe Peano) 开发了第一条空间填充曲线 [25]，这反过来又启发了大卫·希尔伯特 (David Hilbert) 提出计算机科学中最广泛使用的空间填充曲线之一 [15]。

空间填充曲线还在可视化领域中得到应用，将高维数据集映射到一维域，以比较数据集 [8, 44]。弗兰克等人。 [11]使用它们进行与我们类似的时空可视化，并相互比较几条曲线的适用性。大多数空间填充曲线纯粹是出于几何原因且不了解数据。达夫纳等人是少数例外。 [7] 和周等人。 [46]提出了数据感知空间填充曲线。

正如我们在 4.3 节中所示，上述方法都不能保持标量场的特征完整。

其他导出线性顺序的方法适用于点集并使用分层聚类[12]或多维缩放[32]。它们并不直接适用于标量场。

3 时间合并树状图

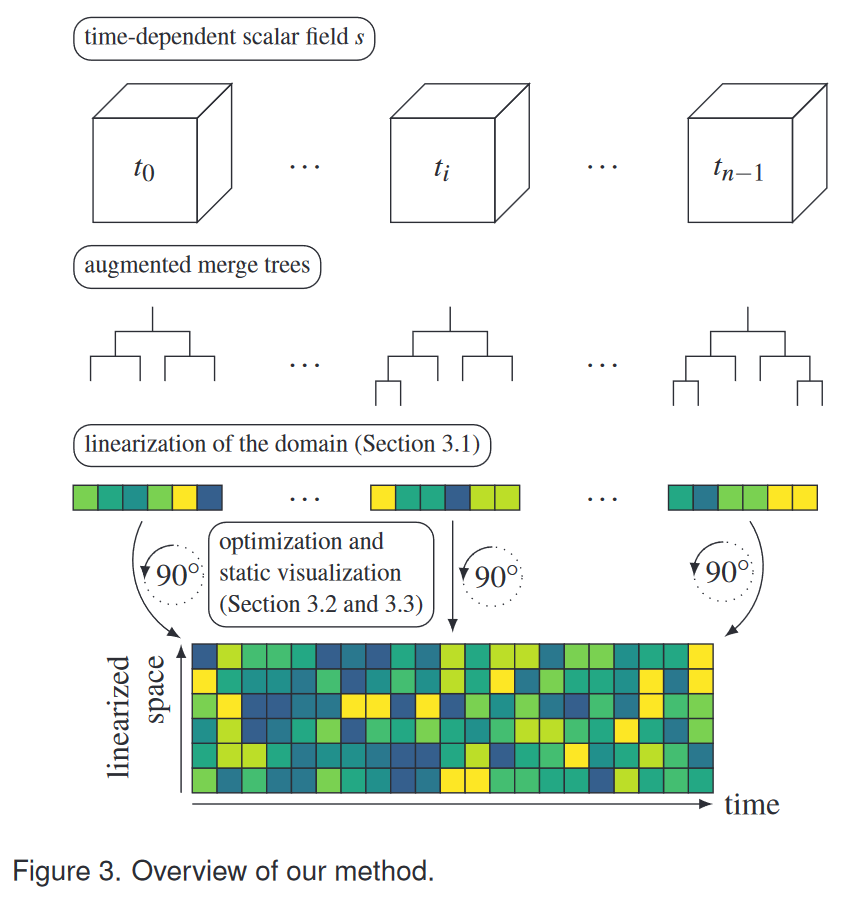
我们提出了一种基于标量场合并树（第 3.1 节）对标量场进行线性化的方法（图 3）。我们表明，该方法保留了合并树拓扑，因此保持了特征完整。连续时间步的映射被优化，以尽可能接近标量场的动态（第 3.2 节）。优化的一维映射被组合成基于像素的静态可视化（第 3.3 节），我们称之为时间合并树图。我们认为应给出以下内容：

• 一系列由 n 个标量场 s(x,t) 组成的数据集，其中时间 t 范围是 [t0,…,tn-1]。每个时间步包含 m 个数据样本。
• 每个时间步对应的增强型合并树 M ∈ [M0,…,Mn-1]。我们使用开源库 Topology Toolkit（TTK）[39] 中现成的算法来计算这些合并树。

3.1 映射单个时间步长：$R^d\to R$

考虑在某一时间步下，一个d维的标量场s及其合并树M。我们的目标是找到一个函数g：$R^d\to R$，将给定标量场s中每一个原始样本位置$x\in R^d$映射到输出标量场 $f$ 的一维样本位置$x\in R$。这是一个对域进行线性化的操作，同时保持样本的函数值不变。直接地，我们将输出设定为整数位置，即$g：R^d\to [0,...,m-1]$。这样做的好处是有助于后续将结果转换成像素。

在非常温和的假设下，我们新构造的输出标量场具有与输入标量场相同的合并树 M。这意味着，我们在输出中看到的最大值与输入的分割树中的最大值一样多（或者与连接树中的最小值一样多）。这对于在最终结果中保留最小值/最大值（气候数据中的旋风、流量数据中的涡流等）描述的特征至关重要。我们在补充材料中展示了这个合并树标识属性。

我们通过 M 的深度优先遍历导出映射 g。在算法的每个阶段，我们维护未分配样本位置的连续输出范围 [xL, xR]，以用于树遍历中的所有即将到来的节点。以下解释附有图 4 中的插图，算法 1 中给出了伪代码。

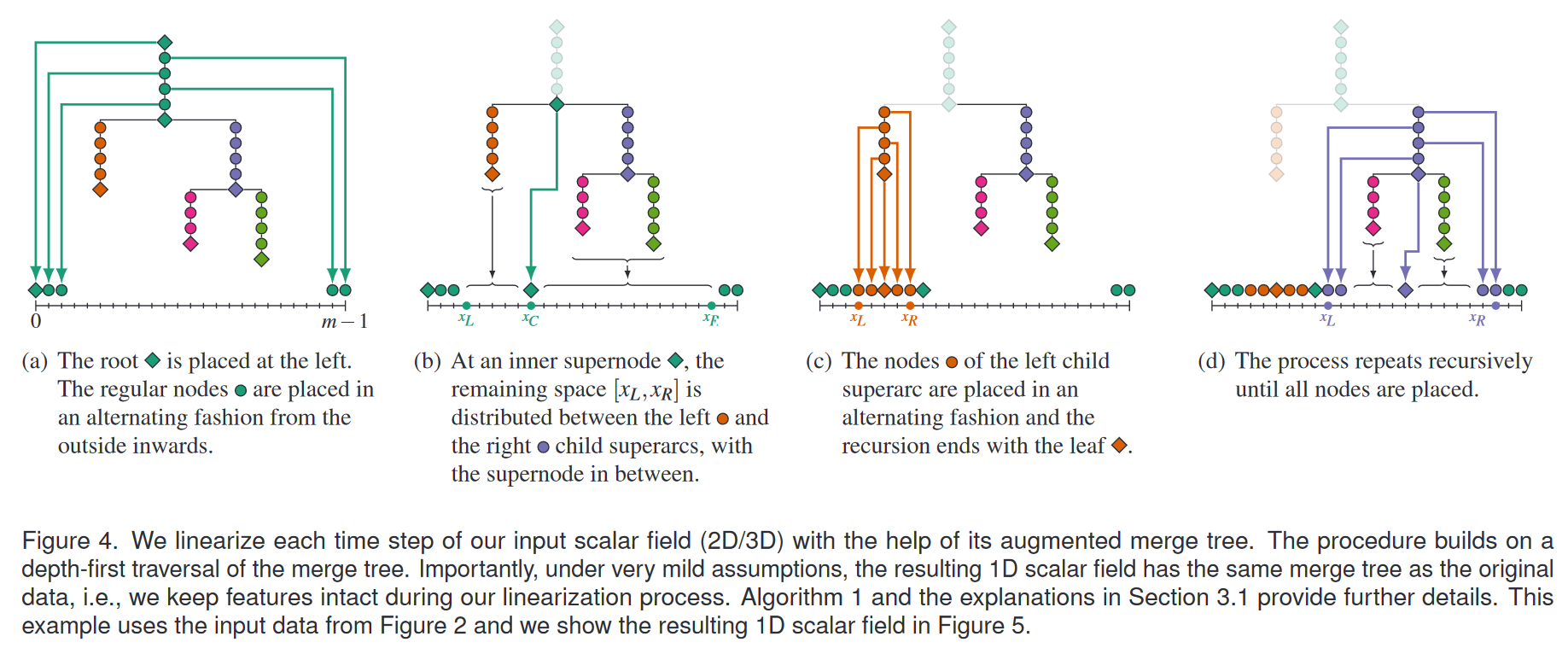
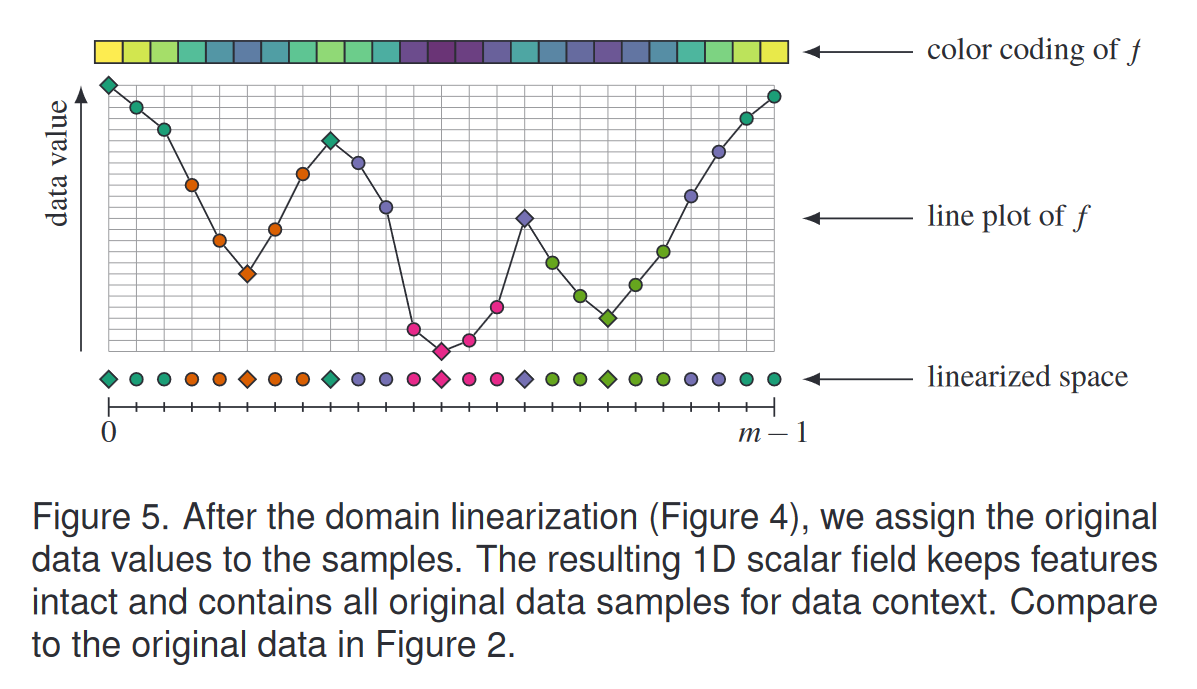
根节点 我们从 $x_L=0$ 和 $x_R=m-1$ 开始。根节点放置在输出范围的左侧，位置为$x_L$（图4(a)）。之后，未分配样本位置的有效范围在$x_L=1$与$x_R=m-1$之间。

超弧的遍历 超弧的规则节点从外向内以交替方式放置在剩余范围 $[x_L,x_R]$ 中：第一个节点放置在右侧的$x_R$处，第二个节点则放置在左侧的xL处，然后再次回到右侧$x_R=x_R-1$，依此类推。图4(a)展示了这一过程。从右侧开始是一个实施选择：我们同样可以从左侧开始，甚至可以随机选择起始边，这都不会影响表示相同合并树的属性。

在遍历过程中，我们持续更新范围$[x_L,x_R]$（参见算法1中的ProcSuperArc()和PlaceNode()函数）。当到达下一个超节点（supernode）时，该过程结束。

在超级节点进入递归 M 的所有内部 1 超节点都有两个子超弧。因此，我们必须在 $[x_L,x_R]$ 中放置三个实体：两个子超弧和超节点本身。我们需要将超级节点放置在其两个子超级弧之间，以保持与输入数据中相同的拓扑。要看到这一点，请回想一下，子超弧代表在超节点处合并或分裂的超级别集或子级别集的连接组件。仅当超级节点与其两个子节点相邻（即位于它们之间）时，才会发生这种情况。假设首先遍历的子节点共有 $n$ 个节点，则超级节点将放置在$x_C=x_L+n$处。然后递归处理子超弧：第一个子超弧填充范围$[x_L,x_C-1]$，第二个子超弧填充范围 $[x_C+1,x_R]$。图 4(b) 说明了这一点。

子超弧的顺序起着有趣的作用。重要的是，任一顺序都会创建一个具有与原始数据相同的合并树的函数。然而，选择首先遍历哪个子节点的灵活性允许优化各个时间步之间相对于数据的整个演化的映射，请参见第 3.2 节。

在叶节点处结束递归 叶节点终止递归。此时，在算法中，只有 $x_L=x_R$ 处的单个空间为要分配的叶子开放。

3.2 映射所有时间步：$R^{d+1}\to R^2$

通过线性化将空间维度压缩到 1 后，我们可以使用显示器的第二个维度来显示时间。例如，我们可以将时间步长垂直定向并从左到右排列。这提供了对数据动态的深入洞察。

在标量场中移动的特征本质上在空间和时间上是一致的，即它们的值和位置变化是平滑的。基本上所有自然现象都是如此，例如流体流动、分子动力学、天气和气候等等。当将这些现象转换为数据时，空间和时间采样分辨率发挥着作用：只有在尊重奈奎斯特频率的情况下，特征才能得到适当的表示。

空间域的任何降维都会限制特征的空间移动。我们的线性化也是如此。此外，以下方面在连续的时间步骤之间可能会有所不同：特征的数量和大小、合并树的层次结构和深度，以及特征可能合并或分裂。尽管存在这些问题，我们的目标是尽可能准确地描绘数据的动态。这个问题陈述部分与在平面上布置跟踪图 [18, 45] 或任何图 [3] 有关。请注意，我们明确避免使用合并树的跟踪信息，因为这会产生非常高的计算成本[23]。

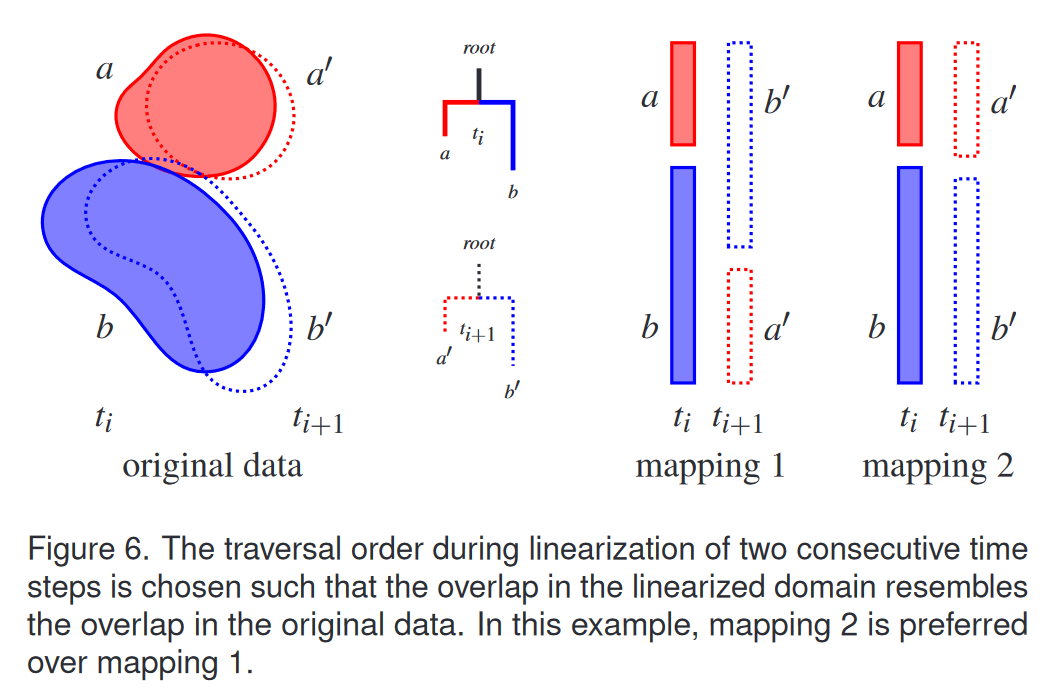
幸运的是，第 3.1 节中的线性化算法为我们提供了如何安排特征的一些自由，以便我们可以最大化时空特征的一致性：当遇到内部超节点时，我们可以决定处理其两个子超弧的顺序。图 6 使用包含 $t_i$ 中的两个子树区域 a 和 b 作为根的子超弧的数据集说明了这一点。这些区域在时间步 $t_i$ 和 $t_{i+1}$之间轻微移动并改变其几何形状。让我们将它们表示为 $t_{i+1}$ 中的$a^{\prime }$和 $b^{\prime }$。不失一般性，我们可以固定在 $t_i$处对树的遍历，使得 a 出现在 b 之前。现在我们有两个选择在 $t_{i+1}$ 处遍历树：要么 $b\prime$ 在 $a\prime$ 之前（映射 1），要么相反（映射 2）。重要的是要明白，我们实际上并不知道这些地区的“名称”；每个时间步都有自己的合并树并且独立线性化。然而，我们确实知道每个映射相对于原始数据中区域重叠的重叠量。在原始数据中，区域$a$和$a^{\prime }$以及$b$和$b^{\prime }$基本上重叠。对于线性化数据，映射 2 是首选选项，因为它的重叠比映射更好地类似于原始数据中的重叠。

3.2.1 离散优化问题

令 $S\in M_t$ 和 $T\in M_{t+1}$为两个连续时间步的合并树中的子树。我们测量它们的重叠（参见 Silver 和 Wang [35]）$$p(S,T)=|S\cap T|(1)$$ 作为属于两个子树的节点（数据中的样本点）的数量。我们注意到，这在原始域和线性化域中是可以独立计算的，并且我们将这些度量分别表示为 $p^{nD}$ 和 $p^{1D}$。

我们试图捕捉原始数据和我们的映射之间子树重叠 $$d(S,T)=(p^{nD}(S,T)-p^{1D}(S,T){)}^2(2)$$ 的差异。考虑到所有时间步长和所有子树，我们测量所有连续时间步长对中所有子树对的重叠差异之和：
$$E=\sum _{t=t_0}^{t_{n-2}}\sum _{S_j\in M_t}\sum _{T_k\in M_{t+1}}d(S_j,T_k).(3)$$
这给我们带来了一个离散优化问题，其中 E 是要最小化的目标函数，搜索空间由所有可能的合并树遍历顺序形成。

3.2.2 离散优化问题的启发式方法

遍历顺序由一系列二元决策决定：在每个内部超节点，我们必须决定首先处理哪个子超弧。这意味着我们的搜索空间总共包含 $2^N$ 种可能的配置，其中 N 是所有时间步长的内部超级节点的总数。即使对于中等大小的数据集，如此大的搜索空间也是不可能完全枚举的。

局部贪婪启发法对于许多复杂的离散优化问题给出了很好的结果。我们针对上述优化问题提出了这样的启发式。特别是，我们利用了这样一个事实：与较低级别相比，合并树中较高级别的不匹配会由于其较大的尺寸而导致更大的错误。直观上，遍历早期的错位无法通过更改树下部的遍历决策来纠正。

我们提出以下过程：我们将一个初始合并树 Mt 的遍历顺序视为固定的，例如，使用弧在数据结构中存储的顺序。此处可以选择任何时间步长。然后，通过从根开始并在每个内部超级节点建立遍历顺序来优化下一个合并树 Mt+1 的遍历。为此，我们根据方程（3）计算两个子元素对两种可能的遍历顺序的总体目标的贡献。贡献较小的遍历顺序获胜。我们继续处理树更深层的内部超级节点。

确定$M_{t+1}$的遍历顺序后，继续$M_{t+2}$，依此类推。类似地，我们可以从$M_t$时间回到$M_{t-1}$，直到所有时间步骤中的合并树都有固定的遍历顺序。

其实施受益于以下观察。首先，我们可以通过迭代数据一次来预先计算原始标量场中的子树重叠 $p^{nD}$ 。其次，当我们在遍历顺序的搜索空间中导航时，必须经常计算线性化域中的重叠。我们可以利用区间算术直接计算它，而无需迭代数据。为此，我们使用分配给每个子树的最小和最大位置，并计算 $S_j$ 和 $T_k$ 之间的重叠量，作为较小的最大值和较大的最小值之间的差。
$$\begin{array}{rlr}\underset{x_{max}}{\min }& =\min (x_{max}(S_j),x_{max}(T_k))& \\ \underset{x_{min}}{\max }& =\max (x_{min}(S_j),x_{min}(T_k))& \\ p^{1D}(S_j,T_k)& =\max (0,\underset{x_{max}}{\min }-\underset{x_{min}}{\max }+1)& (4)\end{array}$$

最后，请注意，根以下的子树（即整个树）可以从这些计算中省略。任何其他子树总是与整个域重叠。这自然适用于原始数据和线性化数据，并且差异对目标函数没有额外的贡献。

3.3 最终图像的拼接：基于像素的可视化

我们的最终可视化由一个 2D 图像组成，该图像表示一个方向（通常是垂直）的线性空间和另一个方向（通常是水平）的时间。我们使用颜色编码来显示相应的数据值，并将该图像称为时间合并树图。请参见图 3 底部的说明。

如果我们将原始数据的每个样本点表示为单个像素，则图像的最终分辨率将是 m × n，其中 m 是一个时间步中的数据点的数量，n 是时间步的数量。然而，m 通常显着超过显示器的尺寸或 GPU 纹理大小限制，而 n 通常低于这些数字。沿着线性化空间的维度，我们使用子采样将像素数量减少到 GPU 纹理大小限制以下，在我们的硬件上为 4096。沿着时间维度，如有必要，我们使用线性插值来填充显示。

4 评价与讨论

我们通过介绍本文中使用的所有数据集并提供我们的算法各自的运行时间来开始我们的评估（第 4.1 节）。然后我们分析优化方案的定量和定性性能（第 4.2 节）。我们将我们的算法与其他线性化方法（第 4.3 节）和特征跟踪方法（第 4.4 节）进行比较。最后，我们讨论了我们的算法在数据大小和复杂性方面的局限性（第 4.5 节）。

4.1 数据集与运行时性能

我们在本文中使用以下数据集：

Nucleon Zhou 等人用于评估的核子数据集的填充切片。 [46]。该数据集在开放科学可视化数据集集合 [16] 中公开提供，并由德国研究委员会 (DFG) 的 SFB 382 提供。

Ring Franke 等人创建并用于评估的分析数据集.[11]。通过峰值和标准偏差进行参数化，以沿着由中心位置和半径给定的圆生成高斯钟形曲线。除中心位置外的所有参数在开始和结束之间线性变化。

Benzene 使用[36]中描述的分数电荷法计算苯分子周围的静电场。该场的梯度描述了在特定位置给出的正点电荷上的力。

Storms 1999 年 12 月的 1 小时平均海平面压力异常。瞬时数据是从哥白尼气候变化服务 (C3S) 气候数据存储 [14] 中提供的 ERA5 再分析数据集获得的。我们按照 Deroche 等人用于检测旋风的数据处理程序减去 8 天的平均值。 [9] 并对结果应用轻度高斯平滑。

Cylinder Camarri 等人通过直接数值 Navier Stokes 模拟获得了方形圆柱体后面的流动。 [4]。 von Funck 等人对该流程的统一重采样版本。 [42]已用于计算 Okubo-Weiss 准则 Q = 1/2(∥Ω vortex acti ∥2 −∥S∥2)，这是一个与时间相关的标量场，指示 Q > 0 的区域的活力，并使用在本文中。

Tangaroa Popinet 等人使用 Gerris 流求解器 [28] 对研究船 Tangaroa 模型背后的流动进行了模拟。 [29]。我们使用 ETH 计算机图形实验室可视化数据集集合中提供的重采样版本的速度大小 [13]。

表 1 给出了分辨率、简化阈值、拓扑复杂度和运行时间。我们注意到，TTK [39] 中的大部分运行时间都花在合并树的提取和简化上，这可以通过并行化来显着加快我们对 Tangaroa 数据集所做的时间步长。通过运行 18 个并行线程，我们获得了 8 倍的加速系数。

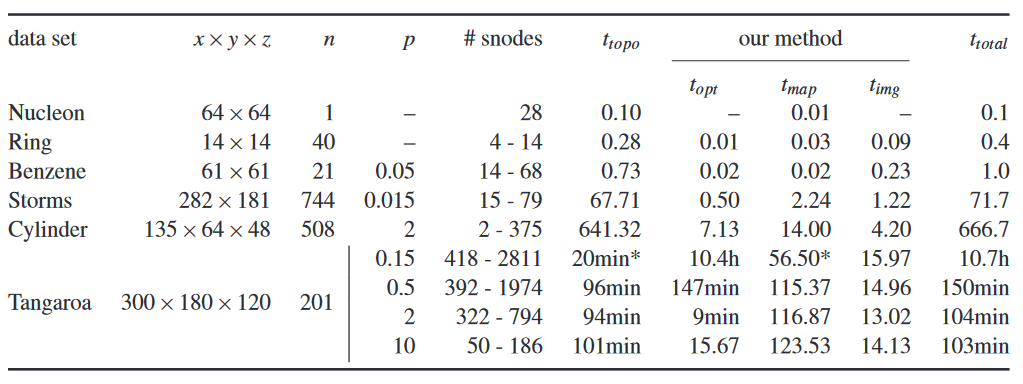
表 1. 我们的数据集概述，包括维度 (x × y × z)、时间步长 (n)、持久性阈值 p（占数据范围的百分比）以及简化合并树中的超级节点数量 (# snodes)。预处理（使用 TTK [39] 提取和简化合并树）的运行时间总结为$t_{topo}$。我们的方法的运行时间详细给出了每个单独阶段：优化 ($t_{opt}$)、线性化 ($t_{map}$) 和图像创建 ($t_{img}$)。除非另有说明，所有计时均以秒为单位，并以单线程测量；带 * 的时间来自 18 个线程的并行运行。我们使用的工作站配备两个 18 核 2.3GHz Intel Xeon E5-2697 v4 处理器和 256GB 主内存。较短的运行时间是通过平均 10 次运行来获得的。

4.2 目标函数的分析

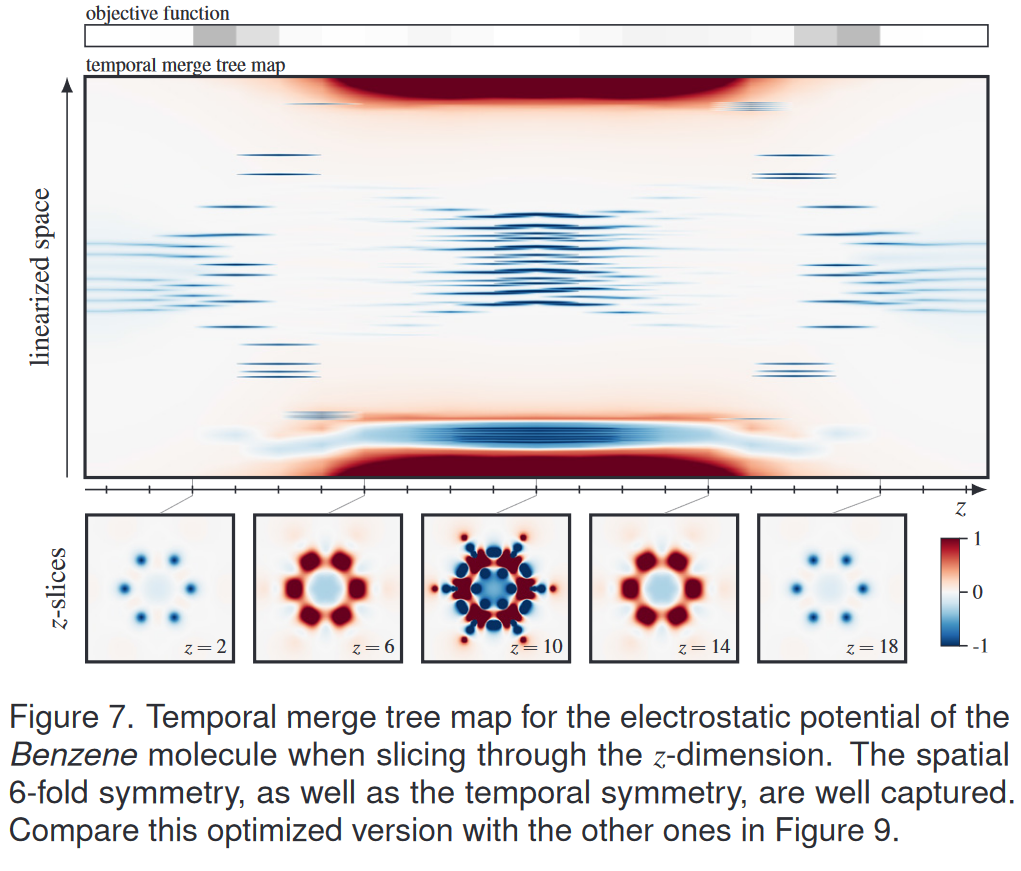
为了深入了解我们的优化方案，我们选择了一个不平凡的数据集，我们可以期望获得特定的输出。Benzene 数据集代表苯分子周围的静电势，并在 xy 平面上表现出众所周知的 6 重对称性。它是一个静态 3D 标量场，我们选择 z 维度来对“时间”上的数据进行切片，使其成为一个 2D 时间相关场。五个代表性的 z 切片显示了图 7 中的设置。在 z = 10 时，我们看到静电势最强的值，因为该切片直接切穿了分子本身。随着距离 z = 10 的距离增加，场在两个方向上都变弱，即，除了空间 6 重对称性之外，我们还具有“时间”对称性。

我们使用连接树来分析该数据，即连接树的叶子是静电势的最小值。

图 7 中的时间合并树图显示了我们算法的优化输出，并很好地揭示了时间和空间对称性。在 z ≤ 4 的切片中，空间 6 重对称性很容易辨别，其中 6 条水平蓝线代表最小值，我们也将 z = 2 切片中的六个不同的蓝色区域视为最小值。我们在 z ≥ 16 的切片中看到相同的行为，这成功地揭示了数据中的时间对称性。它还表明我们的优化方案以非常一致的方式处理 z 维度两端几乎相同的数据。

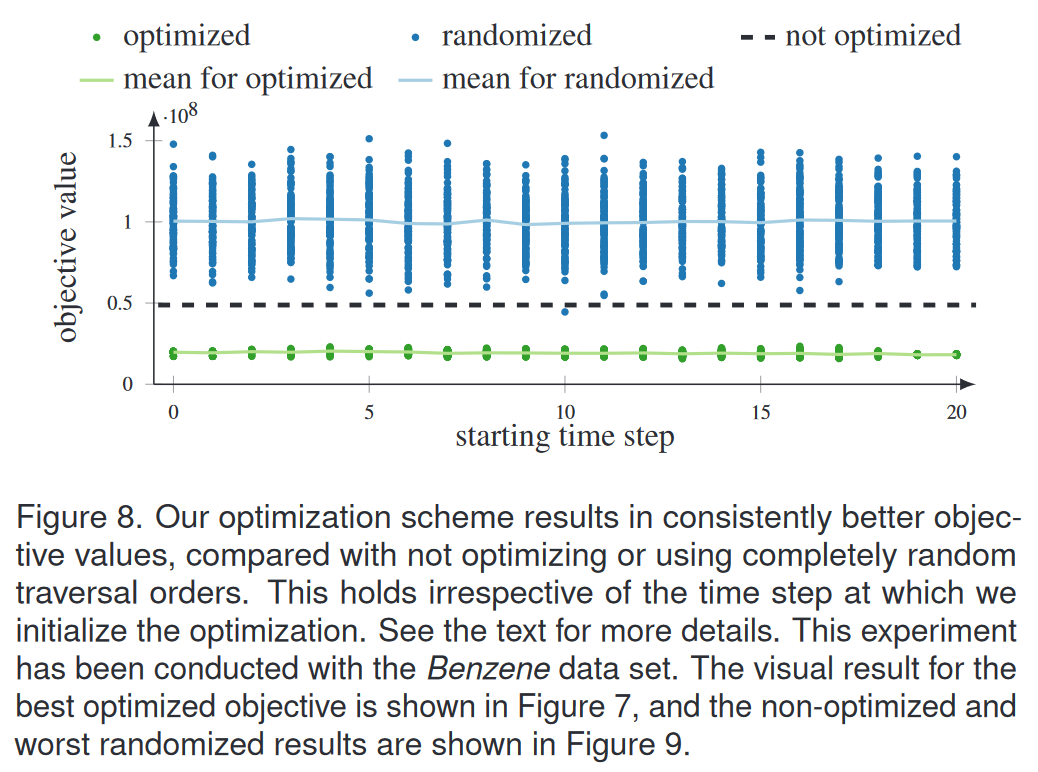
为了定量评估优化方案，我们设置了以下实验：对于每个时间步，我们启动优化方案100次；通过随机化该时间步中合并树的遍历顺序，每次运行都使用不同的起始条件进行初始化。我们记录了每次运行的等式 (3) 中的目标函数值 E，并在图 8 中以绿色绘制结果。我们将其与其他两个条件进行比较：虚线代表未优化版本的目标函数值，蓝色代表未优化版本的目标函数值。点代表我们随机化所有合并树的遍历顺序的运行。正如我们所看到的，我们的优化以一致的方式实现了明显更好的目标函数值。这也意味着更高的视觉质量：图 9 显示了非优化版本和随机版本的时间合并树图，与图 7 中的优化版本相比，其对称性更少，扭曲更多。

4.3 与其他线性化方法的比较

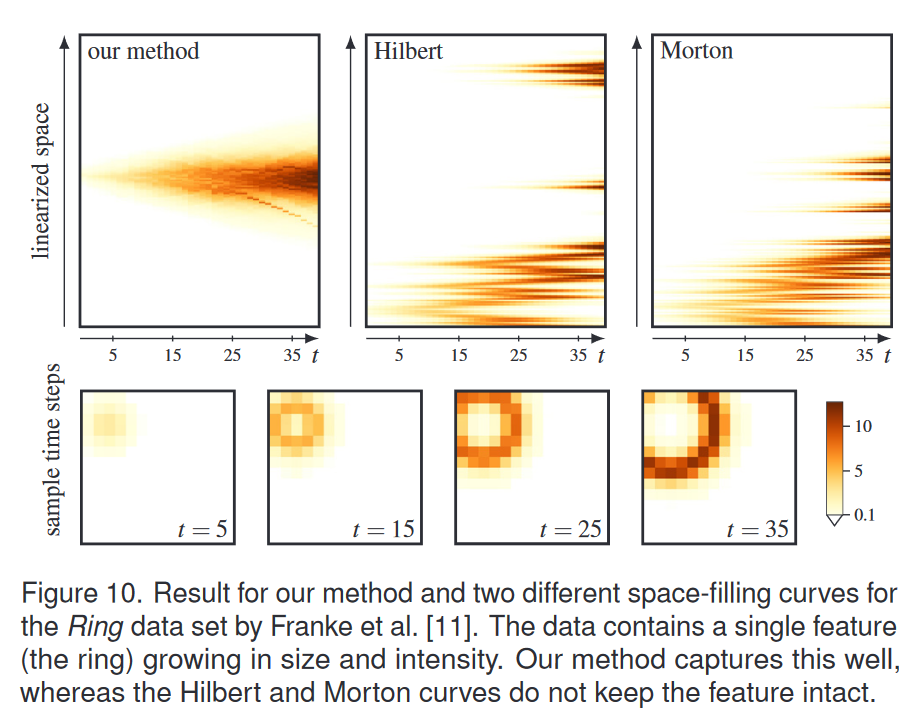
弗兰克等人。 [11]使用空间填充曲线将数据线性化，以形成时空摘要视图。布局与我们的非常相似：线性化空间和时间是该视图的两个维度。为此目的评估了许多不同的空间填充曲线，特别是使用人工环数据集。我们使用作者的代码重新创建了图 10 中的 Hilbert 和 Morton 曲线实验（参见 Franke 等人 [11] 中的图 5a），并将其与我们的结果进行比较。该数据集具有单一特征，即环随着时间的推移而变大，但空间填充曲线无法保持该特征完整并将其足迹分散在空间轴上：原始数据的一致性不通过希尔伯特和莫顿空间填充曲线。另一方面，我们的方法保持了特征的完整性，并且从我们的结果中很容易看出其强度和足迹的增长。

可视化和图形应用程序受益于域线性化的“数据感知”形式。周等人。 [46]提出了数据驱动的空间填充曲线，旨在最小化邻域中数据值的相似性和位置一致性。达夫纳等人。 [7]提出基于上下文的空间填充曲线来改善 2D 图像和视频编码中的自相关性。我们将它们与图 11 中的方法进行比较，我们基本上重新创建了 Zhou 等人的图 6。 [46]使用作者的代码。顶行中线性化的线图显示希尔伯特曲线和基于上下文的曲线不保留特征一致性。乍一看，简单的扫描线方法似乎保持了特征完整，但这是间接的，经过仔细检查，人们可以看到单独的尖峰。 Zhou等人的数据驱动曲线。 [46]设法将大多数较大的数据值保持在一起，但也表现出不同的单独峰值。然而，Nucleon 数据集由一个大特征和顶部的两个小最大值组成，我们的方法忠实地再现了这一特征。

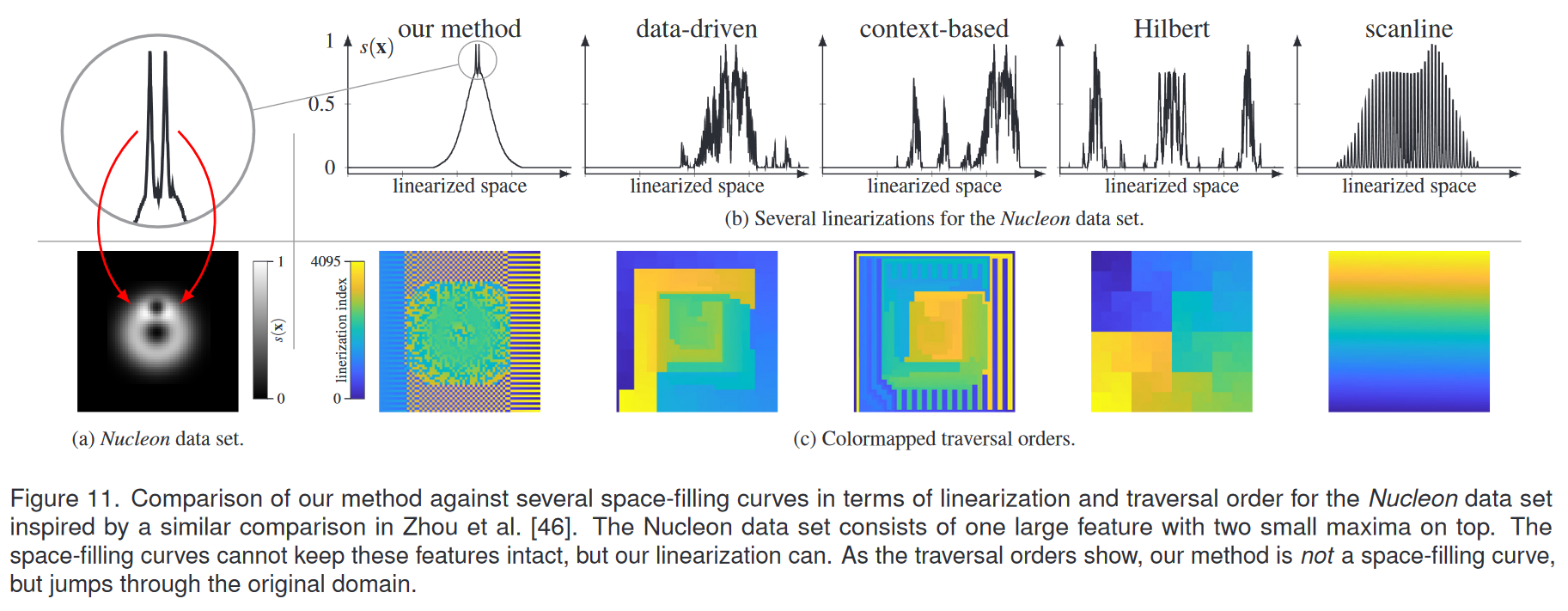
图 11 的底行使用颜色编码方案可视化不同方法的遍历顺序：首先访问蓝色点，最后访问黄色点。这揭示了空间填充曲线的非常有趣的访问模式，并且还再次强调我们的线性化方法不使用空间填充曲线：线性化索引跳过原始数据域。因此，图像和视频编码等应用程序不太可能从我们的方法中受益。相反，我们的目标是特征一致性很重要的应用程序，例如本文中提出的时空摘要视图。

我们使用补充材料中的其他数据集提供额外的比较。

4.4 与其他基于特征的方法的比较

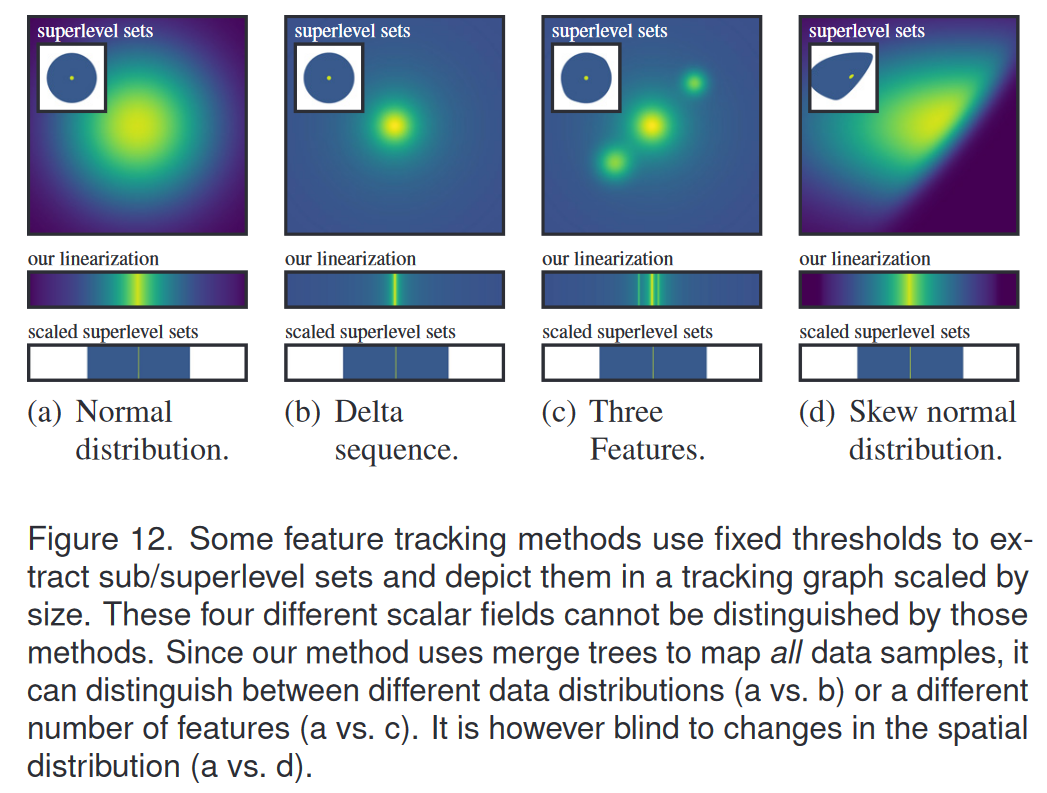
特征跟踪方法[18,22,33,45]的目标之一是尽可能减少数据量；因此，特征的呈现没有其数据上下文。我们在图 12 中详细阐述了与我们的方法的差异，其中我们使用 4 个不同的函数，它们都表现出相同的数据范围 -0.3 ≤ s(x) ≤ 1，但具有不同的分布和空间模式。具体来说，我们将我们的方法与使用子/超级别集的方法进行比较，例如 Lukasczyk 等人的嵌套跟踪图。 [22] 或 Köpp 和 Weinkauf 的时间树图 [18]。我们使用 sa = 0.06 和 sb = 0.9 来提取所有四个示例中的超级别集：这些集的大小相同，即它们覆盖数据中的相同区域。因此，仅关注这些特征的方法无法区分它们。另一方面，我们的方法使用合并树而不是固定阈值，并将所有数据样本映射到线性化域。因此，可以用我们的方法区分不同的数据分布（图12（a）与图12（b））或不同数量的特征（图12（a）与图12（c））。然而，我们的方法忽略了图 12(a) 和 12(d) 之间数据的不同空间分布。

我们的方法可以通过使用离散颜色图进行参数化以模拟嵌套跟踪图[22]，即一些离散颜色分布在数据范围内。它们对应于定义嵌套跟踪图各层的固定阈值。图 13 显示了 Storms 数据集的情况：两种方法都会产生相似的第一印象，但我们的方法清楚地显示出更好的时间一致性。存在增加嵌套跟踪图时间一致性的方法[18]，但其计算要求更高的优化方法无法处理该数据的复杂性。我们的启发式方法以不到一秒的计算量保持了令人满意的时间一致性。

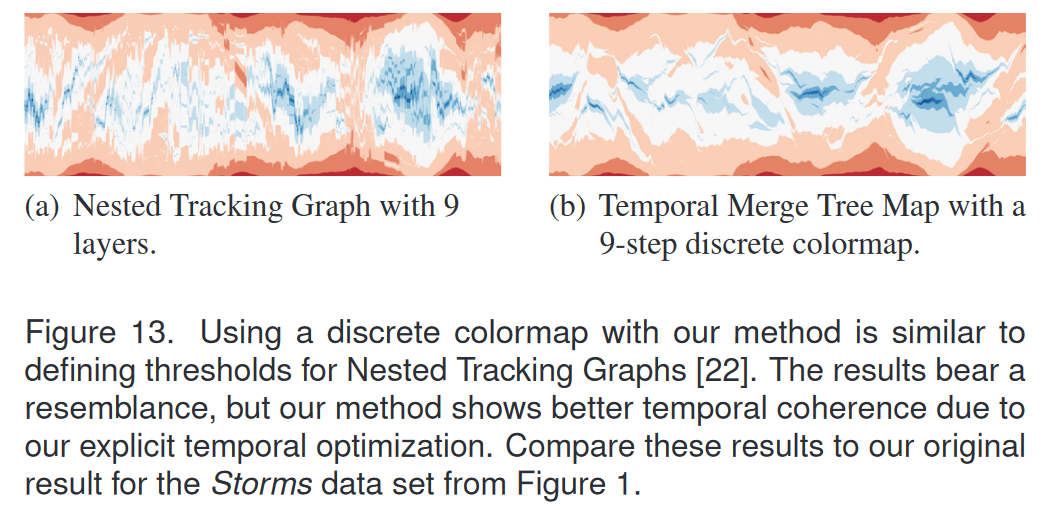
4.5 数据规模和拓扑复杂度的讨论

以下几个方面影响我们的方法对数据集的效果：数据的空间大小、时间大小和拓扑复杂性。这些方面也可能是相互交织的，例如，空间大的数据集在拓扑上也往往很复杂，但不一定。

所有空间维度都被压缩为一并垂直显示。如前所述（第 3.3 节），这通常会导致二次采样。根据数据的空间大小和显示器的可用垂直空间，空间占用较小的要素可能会丢失。对于未来研究自适应采样方法来说，这是一个有趣的途径，它需要与相邻时间步长同步。

临时大数据集对于我们的方法来说并不是一个主要问题。由于时间有其专用的维度，因此在现代显示器上的水平空间耗尽之前，我们可以容纳许多时间步长。在大多数情况下，简单的缩放和平移可以缓解该问题。

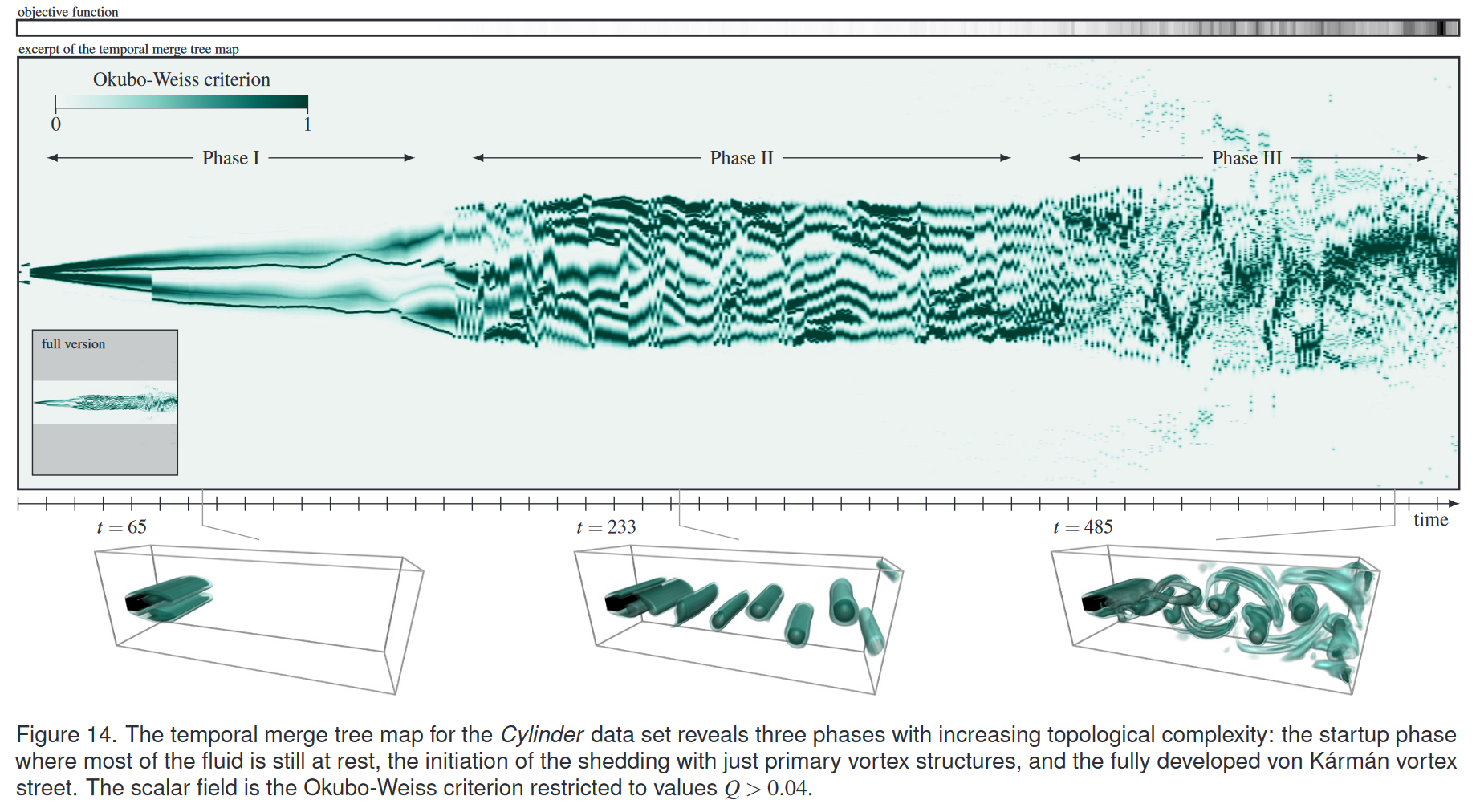
拓扑复杂的数据集对那些旨在向用户显示特征作为可区分实体的基于特征的可视化方法提出了感知挑战：我们只能在任何给定的可视化中区分有限数量的特征。这适用于我们的方法，并且 Cylinder 数据集（参见图 14 和第 5 节）是一个示例，其中拓扑复杂性太高，无法在模拟的后续时间步骤中可靠地区分特征。

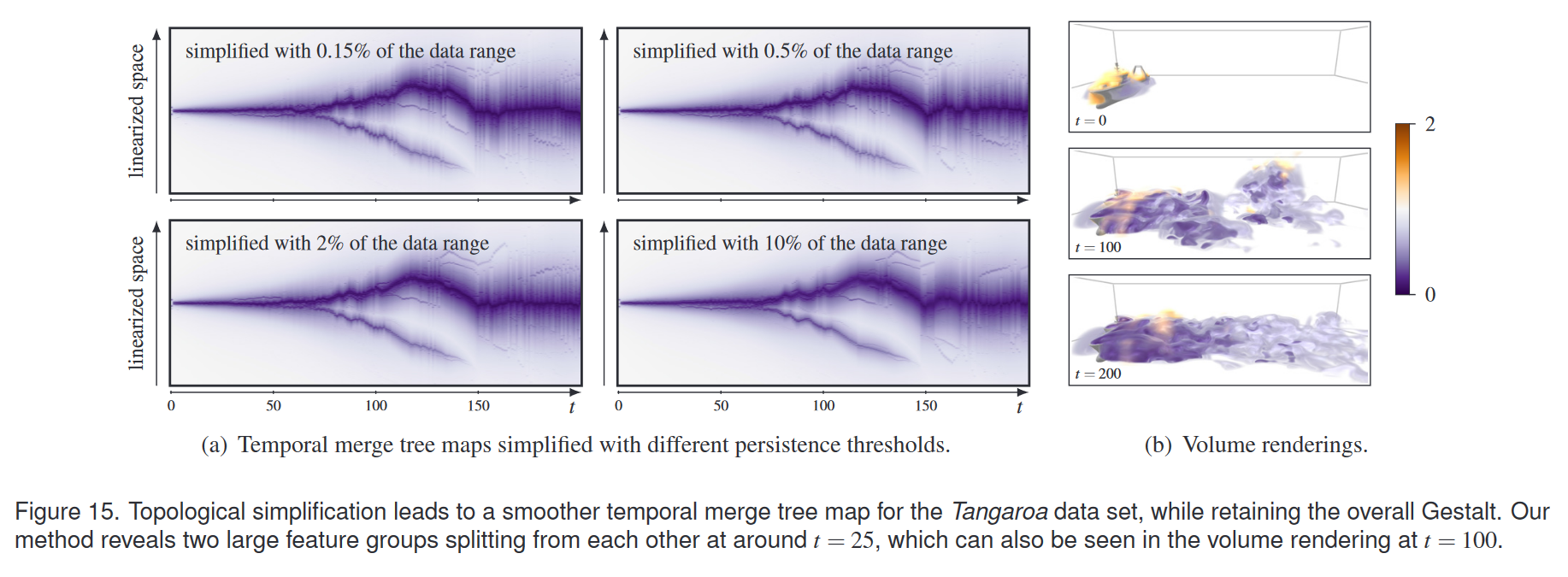
我们使用 Tangaroa 数据集研究拓扑简化的效果。四种不同简化阈值的结果如图 15 所示：增加的简化会导致输出图像中的噪声更少、结构更清晰，同时保留数据的整体格式塔。该数据集的未简化合并树有多达3655个超级节点，这导致优化阶段的运行时间过长。从表1中我们可以看出，拓扑简化显着减少了运行时间。

5 结果

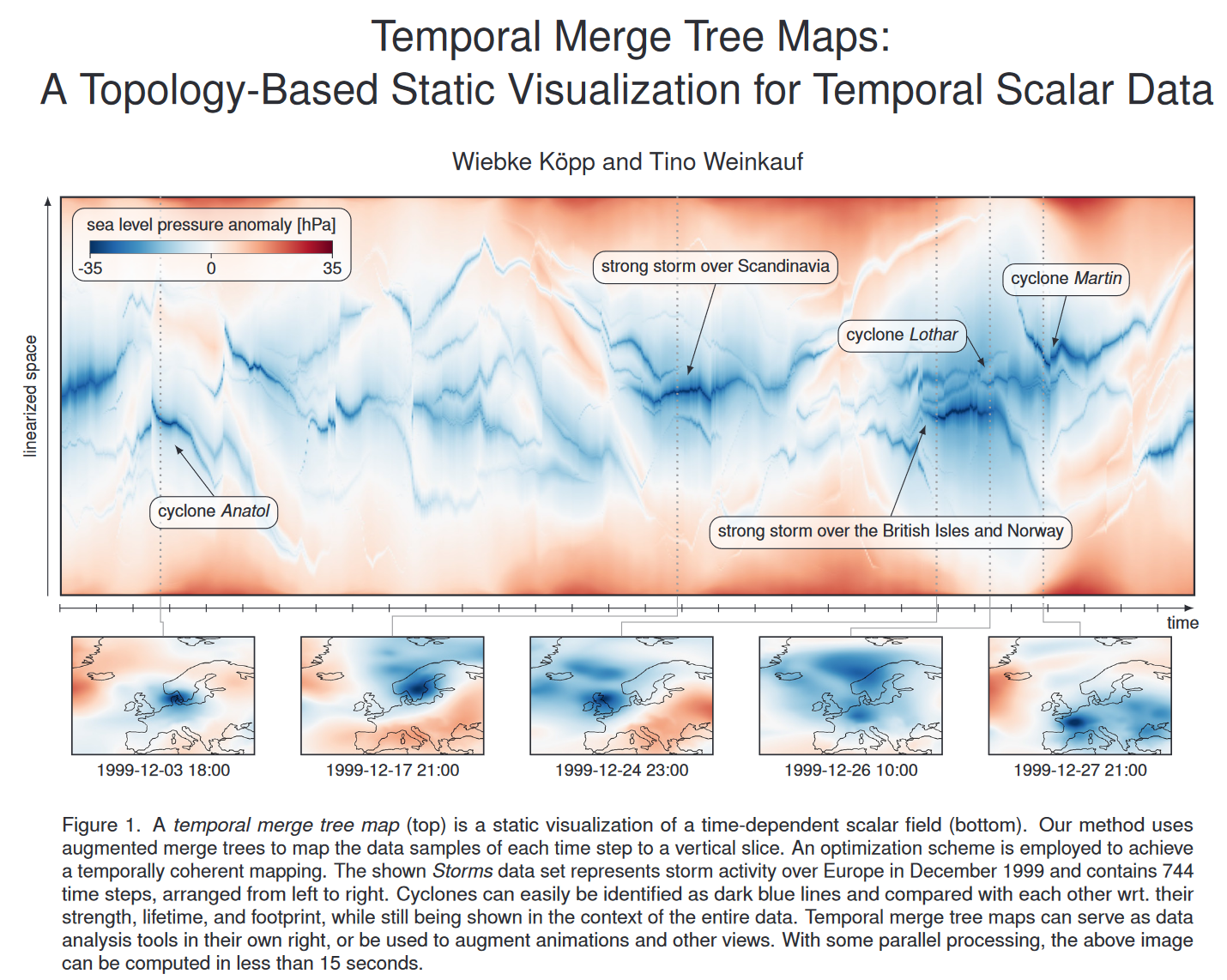
图 1 和图 13 中可视化的风暴数据集是源自大气压力的随时间变化的标量场，这使我们将气旋视为随时间移动的低压区域。它以 1 小时为间隔描述 1999 年 12 月整个月欧洲上空的风暴活动。这是我们时间步数最多的数据集。

1999 年 12 月对欧洲来说是灾难性的一个月：洛塔尔气旋造成 110 人死亡，造成近代欧洲历史上最高的风暴损失（110 亿欧元），使该月的其他猛烈风暴（如阿纳托尔和马丁）黯然失色。

图 1 中的时间合并树图显示了蓝色的低压系统。由于我们的特征保留线性化和时间相干性的优化，这很好地将单个风暴显示为深蓝色曲线。时间合并树图有助于数据分析任务，例如计算风暴、比较其生命周期或足迹大小等。

我们请读者注意 12 月 26 日，几乎所有可视化都变成蓝色，表明当时低压系统占主导地位。同样，12 月 23 日几乎整个地图都会变成红色。这些转瞬即逝的时刻在动画中很容易被错过，但通过我们的可视化可以显着地揭示出来。仅仅进行特征跟踪也无法揭示这些时刻，因为数据上下文将被丢弃。

图 14 所示的圆柱体周围的 3D 流动表现出周期性涡旋脱落，导致著名的冯·卡门涡街。模拟从脉冲启动开始，周期性涡旋脱落随着时间的推移而发展。这意味着，随着时间的推移，流动变得越来越不稳定。这是我们拓扑上最复杂的数据集。

我们的时间合并树图能够揭示模拟的不同阶段。流体在模拟开始时处于静止状态，并且在圆柱体后面慢慢形成再循环区域。这是不发生涡流脱落的启动阶段。一旦再循环区域足够大，涡流就会与其分离并向下游传送。在第二阶段中，我们只看到具有几乎二维行为的主涡结构，即它们的轮廓在翼展方向上保持恒定，并且它们几乎是平行于 z 轴的直管。冯卡门涡街在第三期已全面开发。具有不同轮廓和几何形状的初级和次级涡流结构出现在这个阶段。

请注意，我们正在将该数据集的 4D 时空域转换为 2D 域以进行可视化。天下没有免费的午餐。这个例子表明，我们观察特征演变的能力与数据的拓扑复杂性密切相关。合并树中的超弧越多，识别这些单独的区域、建立它们的时间一致性并随着时间的推移跟踪它们就越困难。三相的平均超弧数量分别为14、37和241。尽管如此，对该数据集进行静态可视化可以提供大量信息，并且是空间体渲染的非常好的伴侣。

图 15 所示的研究船 Tangaroa 后面的 3D 气流捕捉了侧面气流如何受到船只几何形状的影响。这很有趣，因为安装在 Tangaroa 上的几个仪器进行的气象测量可能会受到气流扭曲的影响。我们的时间合并树图揭示了在整个时间范围内持续存在的一种大规模结构。这是船后面和周围的结构。几个不同大小的结构分裂并最终消失。其中最大的是一个特征组，在 t = 25 左右与主要特征组分离，并通过在 t = 145 左右离开域而消失。由于我们的方法提供了所有时间步骤的静态概述，因此我们可以自信地声明此过程仅发生一次并且与周期性涡流脱落不同，而很可能是由初始流动条件引起的。

6 结论与未来工作展望

我们引入了时间合并树映射作为时间依赖标量场的静态可视化。它是基于特征的领域线性化，允许我们将所有的空间维度压缩为一个，同时保持特征的完整性和保持数据的上下文。我们在2D布局中使用了这一点，其中时间维度与线性化的空间维度正交。我们开发了一个最佳保持时间相干性的方案。我们将我们的方法与相关工作进行了比较，并将其应用于多个数据集。

虽然我们的结果与先前的工作相比显示出惊人的时间一致性，并且考虑到降维，我们可以清楚地看到最终结果中的一些时间不连续性。在某些情况下，两个时间步之间的数据只是发生了较大的变化。在这些情况下，更高的数据分辨率可以提供帮助。在其他情况下，某些时间步的超弧尖峰的数量。目前，我们对每个时间步单独进行拓扑简化，这可能会导致时间步之间的尖峰。我们将留待将来的研究来设计一个同时包含所有时间步的全局拓扑简化方案。同样地，尝试其他启发式方法来解决离散优化问题，并研究本文提出的启发式方法是否可以改善基于特征的方法中的布局。未来研究的其他途径包括使用轮廓树而不是合并树，以及上下文感知的子采样[ 1 ]用于创建最终图像。

非常有趣的是，研究如何将我们的概念应用于其他类型的数据，例如向量场或点云，以便我们可以获得与我们现在对具有时间合并树映射的标量场数据相同的时空洞察力。

致谢

作者致谢匿名审稿人Michael Ankele和刘家辉的宝贵意见。这项工作得到了瑞典战略研究基金会( SSF ,项目BD15 - 0082)和瑞典电子科学研究中心( SeRC )的资助。所提出的概念已在Inviwo框架中实现。

参考文献

这篇关于【论文阅读】-- 时态合并树状图：时态标量数据的基于拓扑的静态可视化的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---