从零开始理解AdaBoost算法：设计思路与算法流程（二）【权值更新与加权表决、数学公式】

本文主要是介绍从零开始理解AdaBoost算法：设计思路与算法流程（二）【权值更新与加权表决、数学公式】，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

设计思路

AdaBoost算法属于Boosting算法家族中的一种，其基本思路是将多个弱分类器组合成一个强分类器。

• “强分类器”是指一个分类准确率较高的模型
• “弱分类器”则是指分类准确率略高于随机猜测的简单模型。

AdaBoost的核心思想是通过 加权 的方式逐步提高分类器的性能。

首先来看AdaBoost的数学表达，使用的是 加法模型 ：

$$f(x)=\sum _{m=1}^M{\alpha }_m{G}_m(x)={\alpha }_1{G}_1(x)+{\alpha }_2{G}_2(x)+\cdots +{\alpha }_M{G}_M(x)$$

其中，每一个 $G_m(x)$ 是一个弱分类器，${\alpha }_m$ 是该分类器的权重。

在训练第$m$个弱分类器 $G_m(x)$ 时，我们会记录哪些样本被 错误分类 ，哪些样本被 正确分类 。在下一轮训练时，我们需要增加那些被错误分类样本的权值，同时减少正确分类样本的权值，以此来训练新的弱分类器。这样一来，那些没有得到正确分类的数据，由于权值加大，会受到后续分类器更多的关注。

什么叫样本的权值？如何理解改变？

样本的权值可以理解为在训练集中每个样本的 相对重要性 。

举个例子，假设有三个样本，初始时每个样本的权值都是1/3。如果在第一轮分类中，有两个样本被正确分类，一个样本被错误分类，那么在下一轮中我们会降低被正确分类样本的权值，增加被错误分类样本的权值。

具体来说，假设有三个样本的初始权值如下：

• 样本1：1/3
• 样本2：1/3
• 样本3：1/3

如果在第一轮中，样本1被错误分类，样本2和样本3被正确分类，我们会调整它们的权值为：

• 样本1：2/3 = 4/6（因为分类错误，我们需要增加其权值）
• 样本2：1/6（因为分类正确，我们需要减少其权值）
• 样本3：1/6（因为分类正确，我们需要减少其权值）

此时相当于在样本1具有 4份，样本2和3都 只有1份 ；这样调整权值的目的是在下一轮训练时让分类器更加关注分类错误的样本。

权值如何得到？

AdaBoost采用加权多数表决，即通过加权的 线性相加 来决定最终的分类结果。

权值${\alpha }_m$受到弱分类器$G_m(x)$的分类误差率的影响，当分类误差较小的弱分类器其权值更大，反之，分类误差较大的弱分类器其权值更小。

具体来说：

• 增大分类误差小的弱分类器的权值，使其在表决中起较大的作用；
• 减小分类误差大的弱分类器的权值，使其在表决中起较小的作用。

这些权值的数学表达如下：

$${\alpha }_m=\frac{1}{2}\ln \left(\frac{1-{ϵ}_m}{{ϵ}_m}\right)$$

其中，${ϵ}_m$是弱分类器$G_m(x)$的分类误差率。通过这个公式可以看出，当分类误差${ϵ}_m$较小时，${\alpha }_m$较大；当分类误差${ϵ}_m$较大时，${\alpha }_m$较小。

公式中的特点

这个权值公式有以下两个特点：

1. 自适应调整：权值的调整是自适应的，根据每轮弱分类器的分类效果来决定下一轮的样本权值分布。这样可以确保后续的弱分类器对前面分类错误的样本给予更多关注，提高整体分类器的性能。

2. 误差控制：通过对每个弱分类器的权值进行加权多数表决，可以有效地控制整体分类器的误差。由于每个弱分类器的权值是根据其分类误差率计算的，因此最终组合的强分类器可以显著降低整体的分类误差。

算法流程

第一步：获取数据集

假设数据集$D=\{(x_1,y_1),(x_2,y_2),\dots ,(x_N,y_N)\}$，其中 y ∈ { − 1 , 1 } y \in \{-1, 1\} y∈{−1,1}。

第二步：定义基分类器

基分类器$G(x)$可以是逻辑回归、决策树等。选择逻辑回归时，采用交叉熵损失函数和梯度下降方法进行优化。

第三步：循环训练基分类器

1. 初始化权值：$D_1=(w_{1,1},\dots ,w_{1,N})=(\frac{1}{N},\dots ,\frac{1}{N})$。
2. 训练基分类器$G_m(x)$：如使用逻辑回归，采用交叉熵损失函数和梯度下降方法。
3. 计算分类误差率：$e_m={\sum }_{i=1}^N{w}_{m,i}\cdot I(G_m(x_i)\ne y_i)$。
4. 计算权重系数：${\alpha }_m=\frac{1}{2}\ln \left(\frac{1-e_m}{e_m}\right)$。
5. 更新权值：$w_{m+1,i}=w_{m,i}\cdot \exp (-{\alpha }_m\cdot y_i\cdot G_m(x_i))$，并进行归一化。
6. 更新加法模型：$f(x)=f(x)+{\alpha }_m\cdot G_m(x)$。
7. 判断退出条件：若达到指定的分类器数量或总误差率低于设定值，则停止训练。

第一次训练

假设这是第一次训练，首先需要初始化权值分布 $D_1=(w_{11},\dots ,w_{1i})$，默认每个样本的权值均匀分布为 $\frac{1}{N}$。

然后训练第一个基分类器，例如逻辑回归：使用交叉熵损失函数并通过梯度下降进行优化。

计算分类误差率

1. 计算当前训练集上的分类误差率 $e_m$，范围在 $0\le e_m\le 0.5$：
   $$e_m=\sum _{i=1}^N{w}_{m,i}I(y_i\ne G_m(x_i))$$
   其中，$I$ 是指示函数，当 $y_i\ne G_m(x_i)$ 时，$I(y_i\ne G_m(x_i))=1$，否则为0。误差率不能超过0.5；因为如果错误率大于0.5，可以 反向预测 ，将错误率降低到0.5以下；$w_{m,i}$是权值，是小于1的数。

2. 计算权重系数 ${\alpha }_m$，根据以下公式：
   $${\alpha }_m=\frac{1}{2}\ln \left(\frac{1-e_m}{e_m}\right)$$
   权重系数 ${\alpha }_m$ 的值由分类误差率 $e_m$ 决定。${\alpha }_m$ 越大，说明该分类器的权重越大，即分类效果越好。

函数分析：

• 对于 $\frac{1-e_m}{e_m}=\frac{1}{e_m}-1$，随着 $e_m$ 由0增加到0.5，函数从$+\infty$变到0；
  
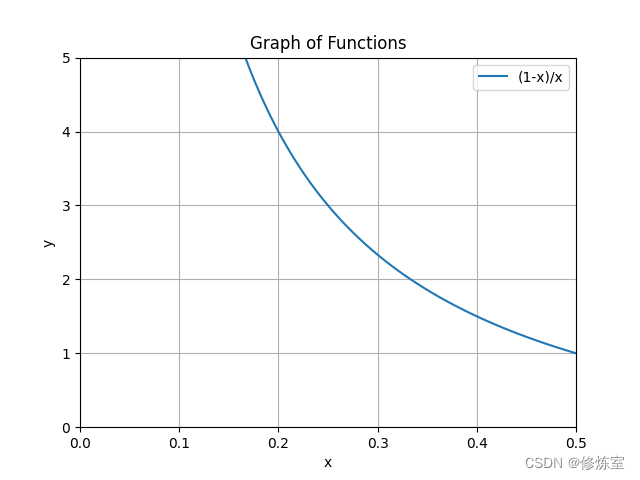
• 对于 $\ln (x)$ 函数，随着 $x$ 从 1 增加到无穷大，$\ln (x)$ 从 0 增加到正无穷。
  

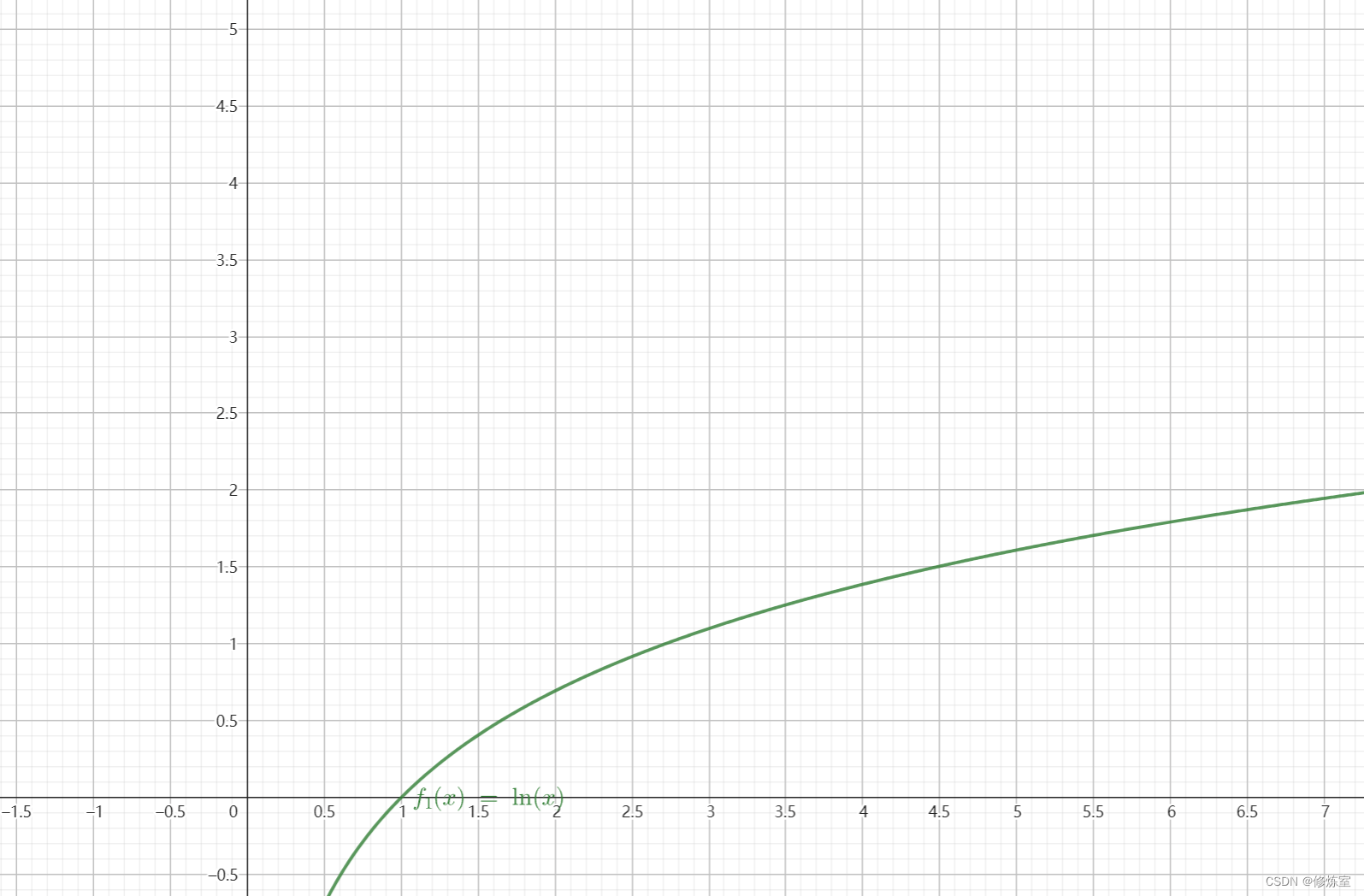
因此，随着 误差率$e_m$ 减小，$\frac{1-e_m}{e_m}$ 增大，样本的权值${\alpha }_m$ 增大。误差率很大的情况下，权重 ${\alpha }_m$ 也会较小，这是因为分类器在这轮的效果不好， 不应在最终的分类决策中占很大权重 。

更新权值分布

根据计算出的分类误差率 $e_m$ 和权重系数 ${\alpha }_m$，更新样本的权值分布 $D_{m+1}$，步骤如下：

1. 计算新的权值 $w_{m+1,i}$：
   $$w_{m+1,i}=w_{m,i}\exp (-{\alpha }_m{y}_i{G}_m(x_i))$$
   式中：

   • 当样本 $x_i$ 被正确分类时，$y_i{G}_m(x_i)>0$，则 $\exp (-{\alpha }_m{y}_i{G}_m(x_i))<1$，权值 $w_{m+1,i}$ 变小；
   • 当样本 $x_i$ 被错误分类时，$y_i{G}_m(x_i)<0$，则 $\exp (-{\alpha }_m{y}_i{G}_m(x_i))>1$，权值 $w_{m+1,i}$ 变大。

2. 进行归一化：
   $$w_{m+1,i}=\frac{w_{m+1,i}}{{\sum }_{j=1}^N{w}_{m+1,j}}$$
   确保所有样本的权值之和为1。

更新加法模型

更新加法模型 $f(x)$：
$$f(x)=f(x)+{\alpha }_m{G}_m(x)$$
至此，第一轮训练完成，得到第一个弱分类器 $G_1(x)$ 及其权重系数 ${\alpha }_1$。

判断循环满足条件

每训练一个弱分类器$G_m$后，进行以下判断：

1. 若基分类器数量已达到预设的最大迭代次数，则停止训练。
2. 若当前集成分类器$f(x)$的分类误差率低于设定的阈值，则停止训练。

在实际应用中，通常会选择第一种方式，以保证训练过程的稳定性和效率。

总结：

AdaBoost是一种通过不断迭代、逐步优化的机器学习算法。通过自适应地调整样本权值和弱分类器权重，能够有效地提升分类器的性能。在实际应用中，适当选择基分类器类型和迭代次数，对于提高算法的分类效果至关重要。

这篇关于从零开始理解AdaBoost算法：设计思路与算法流程（二）【权值更新与加权表决、数学公式】的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---