股票数据集2-纳斯达克NASDAQ 100 分析

本文主要是介绍股票数据集2-纳斯达克NASDAQ 100 分析，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1. 数据清洗

• 用邻近均值的方法，去掉Non_Padding中的NaN数据

  • 这里没用df.fillna(), 因为其只有前向(ffill )和 后向 (bfill) 插值，不适合大量连续的NaN

  • pd转换为np，写一个函数, 返回np数组的空值，lambda的匿名函数返回y轴空值的索引

代码和输出如下：

#数据清洗，去除NaN数据，用邻近均值做填充(padding)
df = pd.read_csv(full) # nrows=3
columns = df.columns
print(df.shape)
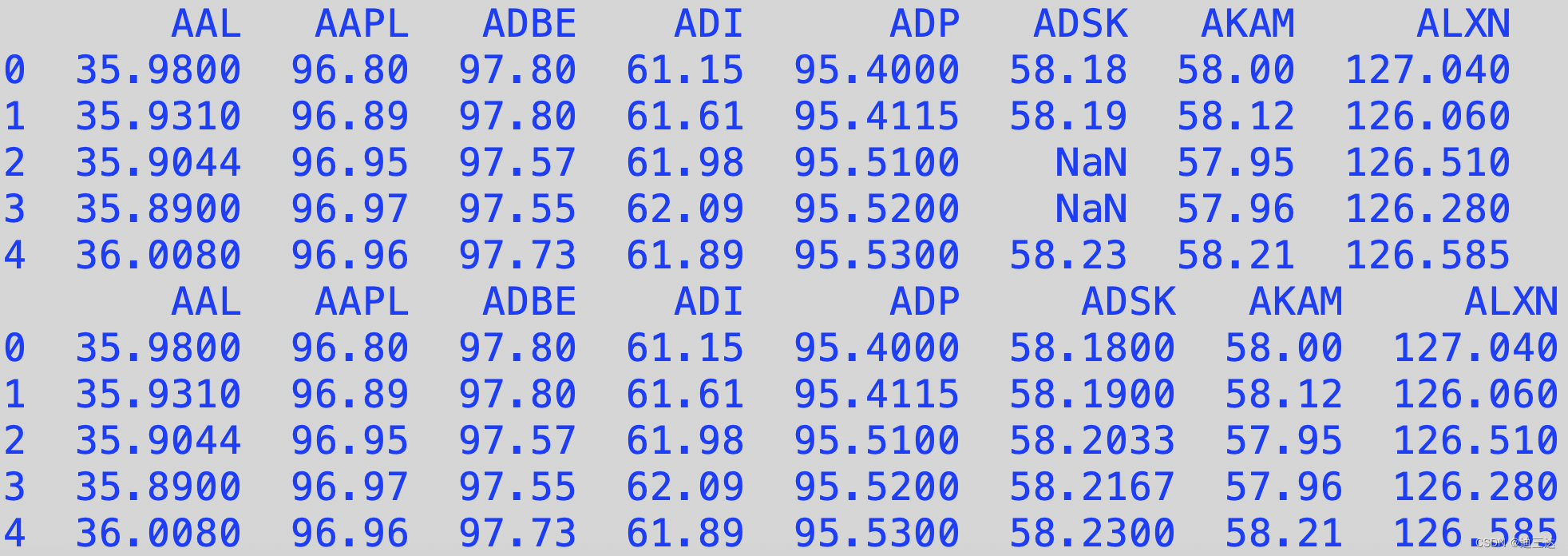
print(df.columns)print(df.iloc[:5,:8])
def nan_helper(y):return np.isnan(y), lambda z: z.nonzero()[0]data = df.to_numpy()
for col in range(data.shape[1]):nans, x = nan_helper(data[:,col])data[nans,col] = np.interp(x(nans),x(~nans),data[~nans,col])df = pd.DataFrame(data,columns = columns)
print(df[:5,:8]) # .round(4)

2.数据可视化

• 画出n个公司的走势，对比指数的走势
  
  
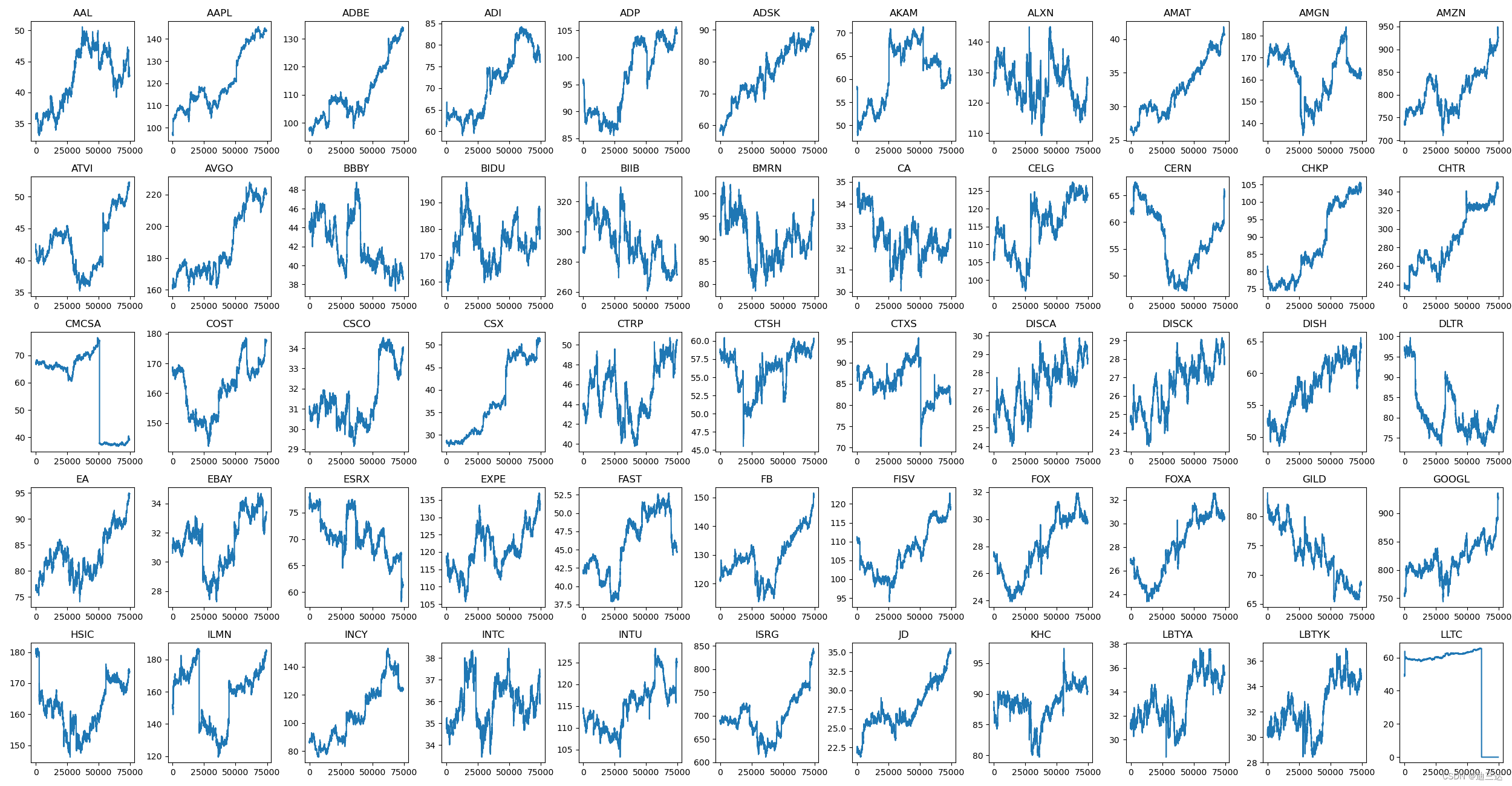
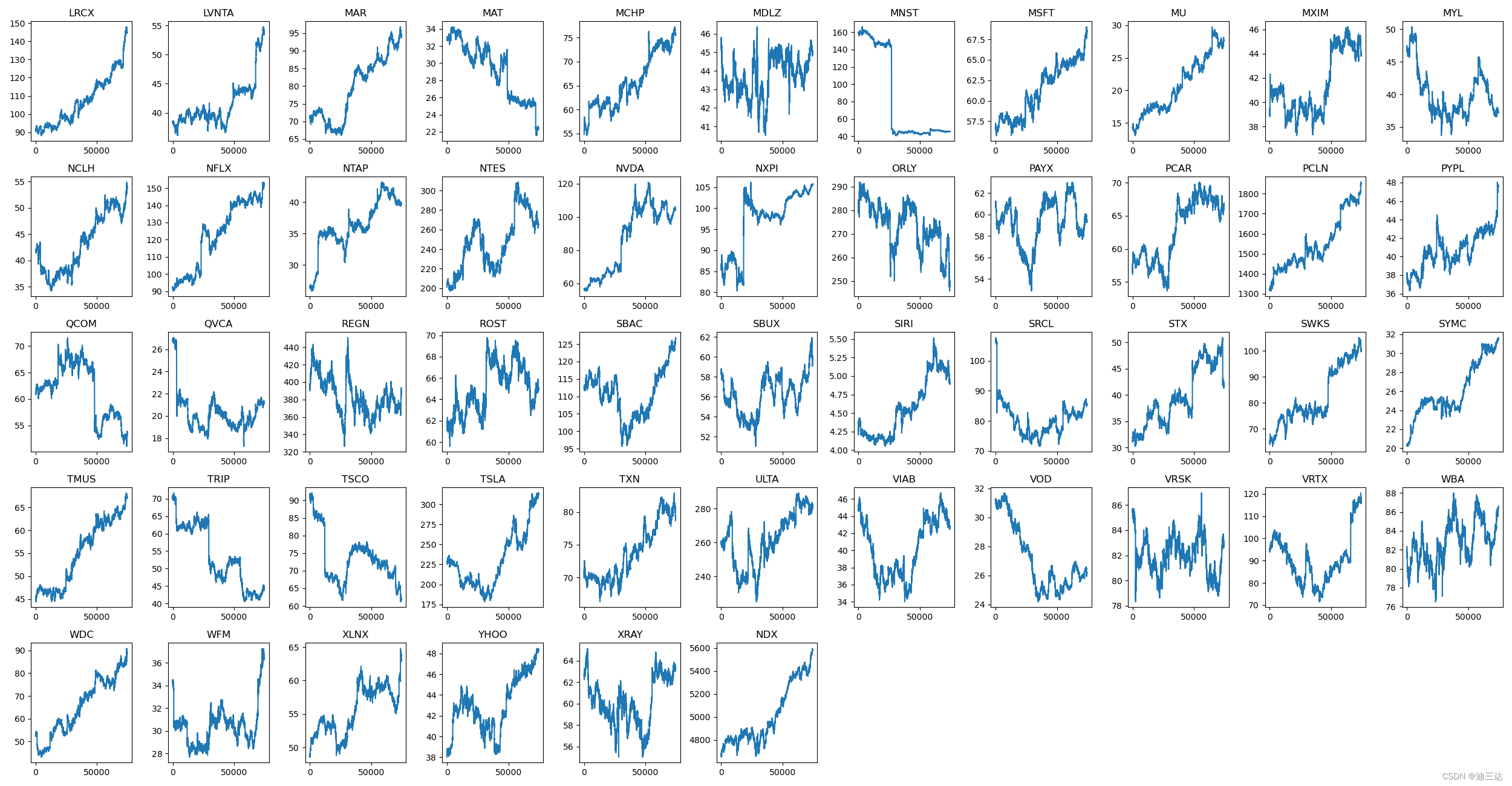
• 画出index, date, close, high, low, open, volume的走势，分析close与其他特征

单只股票AAL的3天走势图（2016-07-26-29），共七个特征:

• 特征1是连续时间，特征2是当天时间

• 后面四个是股价特征（收盘价、最高价、最低价、开盘价），其都是1分钟内的特征值，所以整体相似

• 最后一个是成交量

3.特征选择-相关性分析

3.0 前后特征选择

特征作为算法模型的输入，可以通过一种最原始的方法逐步筛选出有效特征

• 前向选择

  从0开始，根据模型性能表现，逐步添加重要特征

• 后向选择

  相反，从满特征开始，逐各剔除不重要特征

3.1 线性相关系数

• pearson : standard correlation coefficient
• spearman : Spearman rank correlation
• kendall : Kendall Tau correlation coefficient

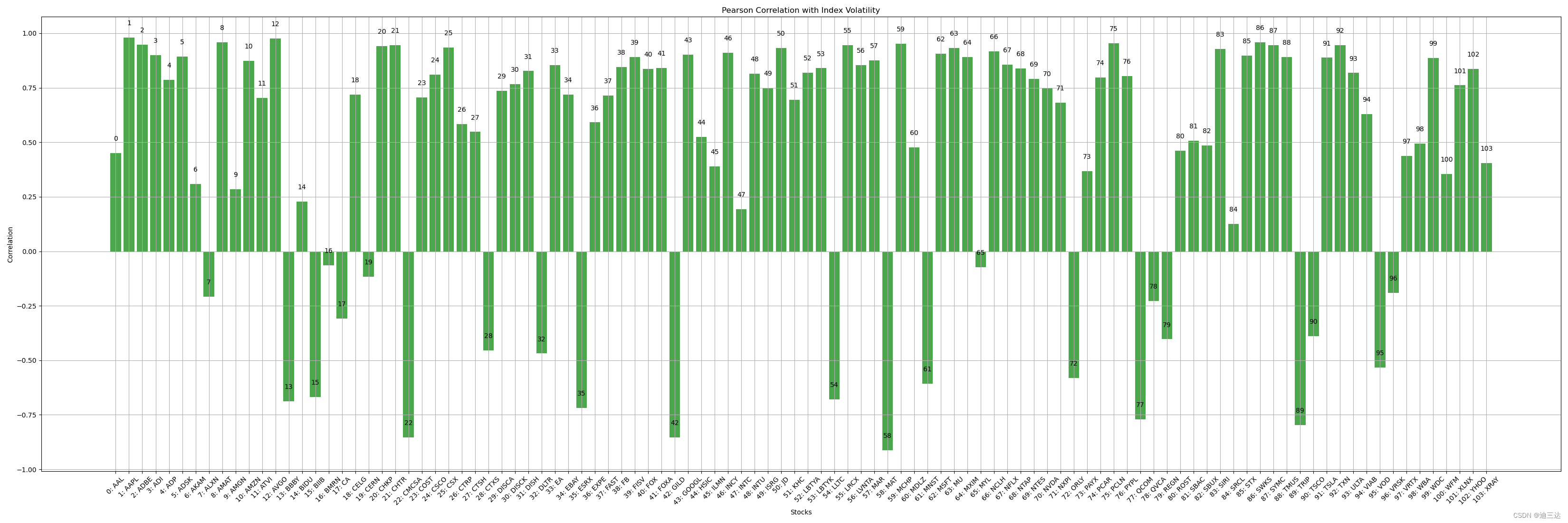
3.1.1 Person (皮尔逊相关系数 )

皮尔逊相关系数（Pearson correlation coefficient）是衡量两个连续变量之间线性关系强度和方向的统计量。

它是一个介于 -1 和 1 之间的值，其中：

• 当两个变量完全正相关时，皮尔逊相关系数为 1。
• 当两个变量完全负相关时，皮尔逊相关系数为 -1。
• 当两个变量之间没有线性关系时，皮尔逊相关系数接近于 0。

代码：

correlations = df.corr(method=‘pearson’)[‘NDX’].iloc[:-1] # Pearson, NDX就是 Nasdaq-100指数

分析此相关系数，可以将正负相关性较小特征股票剔除，如 [-0.25, 0.25]以内的股票

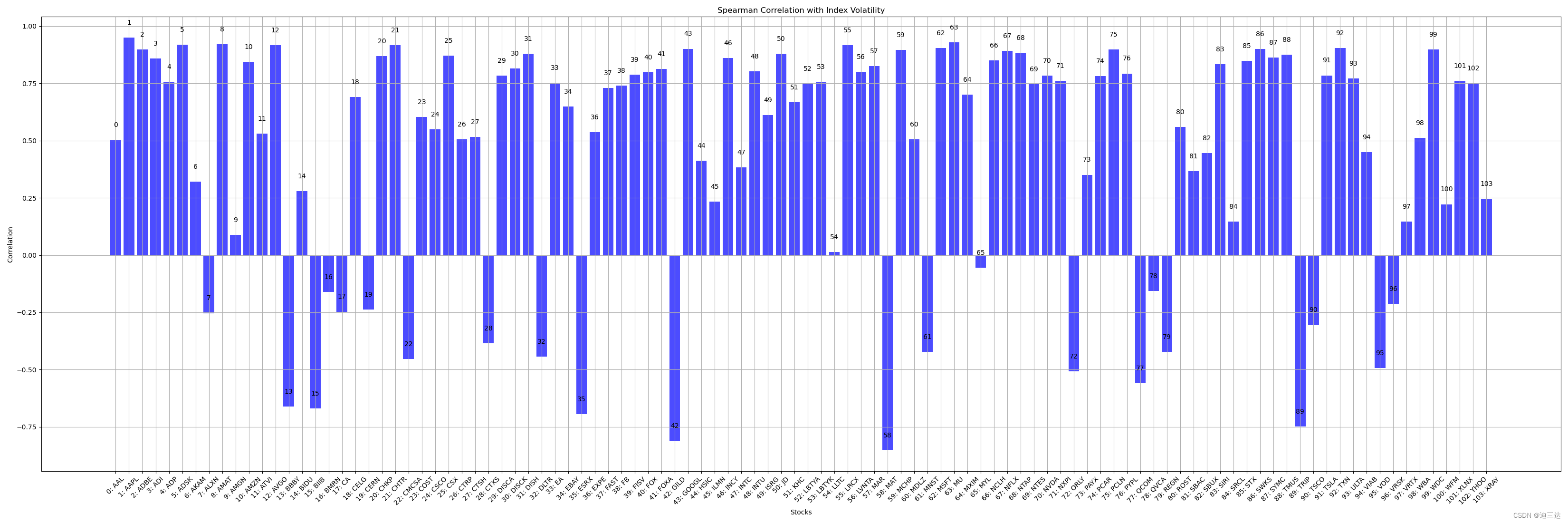
3.1.2 Spearman (斯皮尔曼相关系数)

correlations = df.corr(method=‘spearman’)[‘NDX’].iloc[:-1] # Spearman

斯皮尔曼相关系数（Spearman correlation coefficient）是一种非参数统计量，用于衡量两个变量之间的相关性，不要求变量之间的是线性关键。

Spearman通过比较变量的等级顺序来衡量它们之间的相关性。

斯皮尔曼相关系数的取值范围为 -1 到 1，其中：

• 当两个变量完全正相关时，斯皮尔曼相关系数为 1。

• 当两个变量完全负相关时，斯皮尔曼相关系数为 -1。

• 当两个变量之间没有单调关系时，斯皮尔曼相关系数接近于 0。

与皮尔逊相关系数不同，斯皮尔曼相关系数可以发现变量之间的任何单调关系，不仅限于线性的递增或递减关系。

因此，相比Person, 此方法算出的“不相关”股票更多，如图：

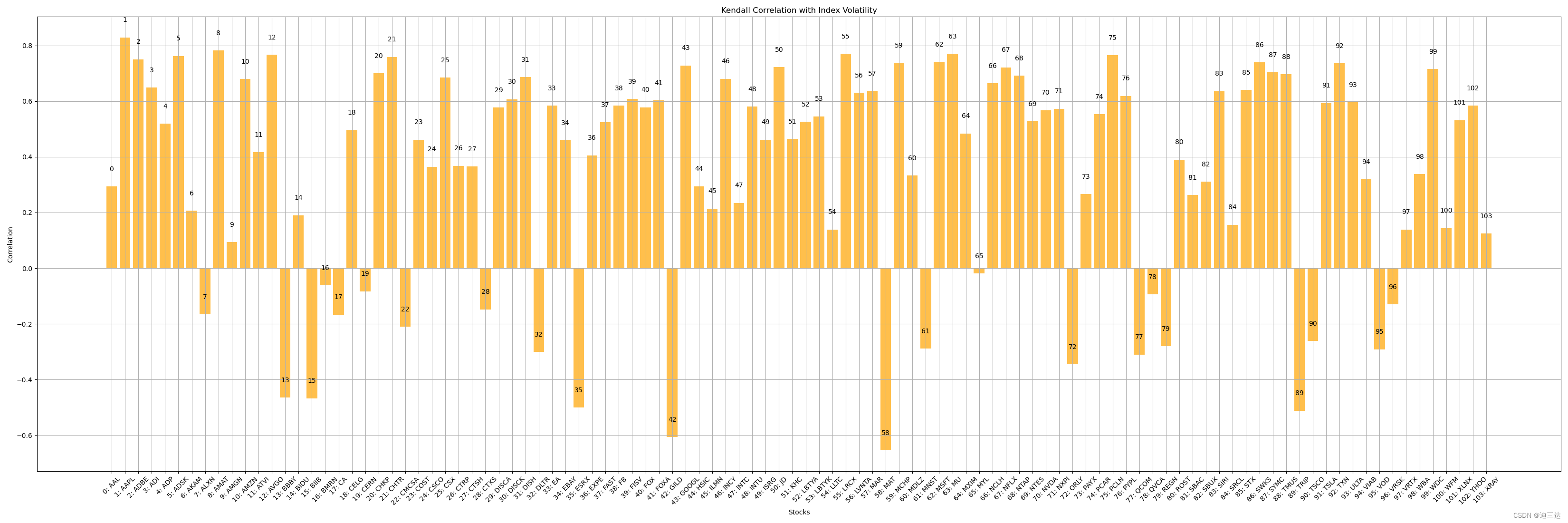
3.1.3 Kendall (秩相关系数)

correlations = df.corr(method=‘kendall’)[‘NDX’].iloc[:-1] # Kendall

Kendall tau是一种用于衡量两个变量之间的非线性关系的统计量。它衡量了两个变量的等级之间的协调性，即它们的等级排名是否是一致的。

Kendall秩相关系数的计算方法是Spearman斯皮尔曼相关系数的改进，但不同之处在于它考虑了等级之间的对比对数（concordant pairs）和不一致对（discordant pairs）。

Kendall在处理有序分类数据或评级数据等情况时更有效，特别是当数据存在等级关系但不满足线性相关的假设时。

Kendall的计算量要大一些(慢)，整体结果和Spearman相同：

后续特征分析还有：

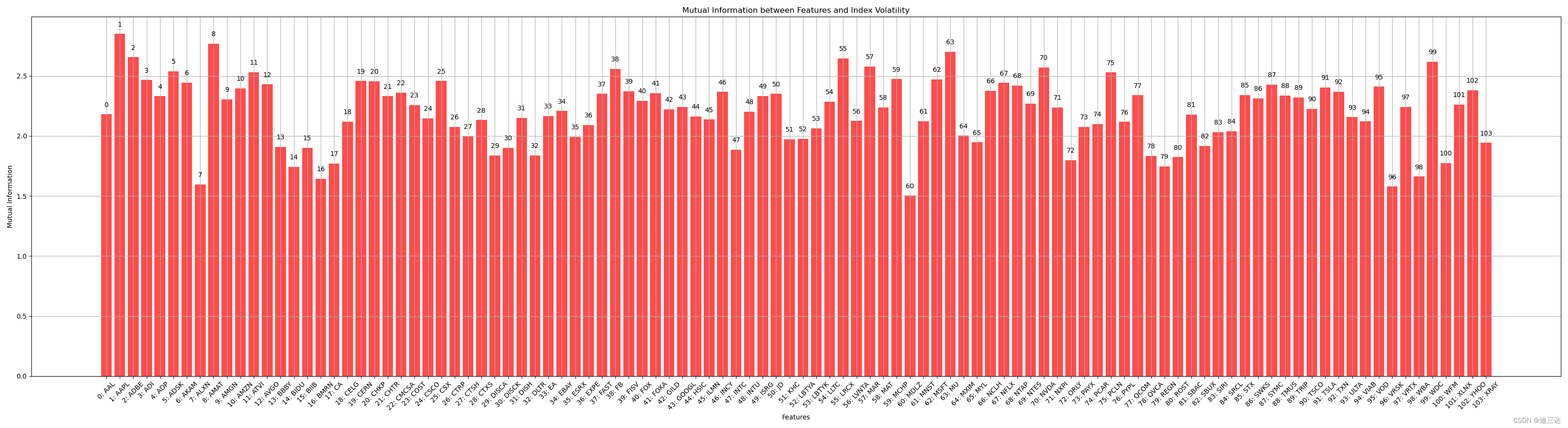
3.2 互信息

Entropy & 熵

3.3 梯度提升树 (Gradient Boosting Trees)

XGBoost (eXtreme Gradient Boosting)梯度下降分析

3.4 主成分分析PCA

协方差矩阵的特征值

对3.3和3.4感兴趣的可以订阅支持我的微信公众号:

股票数据集2-纳斯达克NASDAQ 100 分析

• https://mp.weixin.qq.com/s/8Xhe0ir7QEWIYmtThqo0ew

这篇关于股票数据集2-纳斯达克NASDAQ 100 分析的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---