图论第8天

本文主要是介绍图论第8天，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

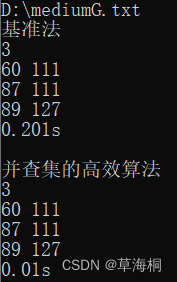
685.冗余连接II

这题需要考虑两种情况：

1.两个输入

2.没有两个输入就是有成环

class Solution
{
public:static const int N = 1005;int father[N];int n;void init(){for (int i = 0; i <= n; i++){father[i] = i;}}int find(int x){return x == father[x] ? x : father[x] = find(father[x]);}int isSame(int a, int b){a = find(a);b = find(b);return (a == b);}void join(int a, int b){a = find(a);b = find(b);if (a == b)return;father[b] = a;}bool lianggeshuru(vector<vector<int>> &edges, int deleteNode){init();for (int i = 0; i < edges.size(); i++){if (i == deleteNode)continue;if (isSame(edges[i][0], edges[i][1])){return false;}join(edges[i][0], edges[i][1]);}return true;}vector<int> huan(vector<vector<int>> &edges){init();for (int i = 0; i < n; i++){if (isSame(edges[i][0], edges[i][1]))return edges[i];join(edges[i][0], edges[i][1]);}return {};}vector<int> findRedundantDirectedConnection(vector<vector<int>> &edges){n = edges.size();int count[N] = {0};// 有两个输入for (int i = 0; i < n; i++){count[edges[i][1]]++;}vector<int> vec;for (int i = n - 1; i >= 0; i--){if (count[edges[i][1]] == 2){vec.push_back(i);cout << i << endl;}}if (vec.size() > 0){if (lianggeshuru(edges, vec[0])){return edges[vec[0]];}else{return edges[vec[1]];}}// 有环return huan(edges);}
};

默写一遍再。其实突然就对这行代码不理解了，需要做个小实验。其实就是后面可以跟一个等式。

    int find(int x){return x == father[x] ? x : father[x] = find(father[x]);}

挺好挺好，默写出来啦！！！思路很重要！！！

class Solution {
public:static const int N = 1005;int father[N] = {0};void init(int num){for(int i = 0;i < num;i++){father[i] = i;}}int find(int x){return x == father[x] ? x : father[x] = find(father[x]);}bool isSame(int a,int b){a = find(a);b = find(b);return (a == b);}void join(int a ,int b){a = find(a);b = find(b);if(a == b)return;father[b] = a;}bool liashuru(vector<vector<int>>& edges,int deleteNode){init(edges.size());// because 1 <= ui, vi <= nfor(int i = 0;i< edges.size();i++){if(i == deleteNode)continue;if(isSame(edges[i][0],edges[i][1])){return false;}join(edges[i][0],edges[i][1]);}return true;}vector<int> huan(vector<vector<int>>& edges){init(edges.size());// because 1 <= ui, vi <= nfor(int i = 0;i < edges.size();i++){if(isSame(edges[i][0],edges[i][1])){return edges[i];}join(edges[i][0],edges[i][1]);}return {};}vector<int> findRedundantDirectedConnection(vector<vector<int>>& edges) {int n = edges.size();int count[N] = {0};for(int i = 0;i < n;i++){count[edges[i][1]]++;}vector<int>vec;for(int i = n-1;i>=0;i--){if(count[edges[i][1]] == 2){vec.push_back(i);}}//俩输入if(vec.size() > 0){if(liashuru(edges,vec[0])){return edges[vec[0]];}else{return edges[vec[1]];}}//有环return huan(edges);}
};

那明天开始做面试题。

这篇关于图论第8天的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---