图论 —— AOV 网与拓扑排序

本文主要是介绍图论 —— AOV 网与拓扑排序，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

【AOV网】

日常生活中，一项大的工程可以看作是由若干个子工程组成的集合，这些子工程之间必定存在一定的先后顺序，即某些子工程必须在其他的一些子工程完成后才能开始。

我们用有向图来表现子工程之间的先后关系，子工程之间的先后关系为有向边，这种有向图称为“顶点活动网络”，即：AOV 网。

一个有向无环图称为无环图（Directed Acyclic Graph），简称 DAG 图，因此一个 AOV 网必定是一个有向无环图，即不带有回路。与 DAG 不同的是，AOV 的活动都表示在边上。

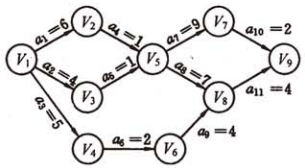
如下图，共有11项活动（11条边），9个事件（9个点），只有一个源点（入度为零的点）和一个汇点（一个出度为零的点），路径的长度是边上活动耗费的时间，则可定义概念——关键路径：从源点到汇点的最长路径的长度，下图中的：1-2-5-7-9 即为一条关键路径，权值的和为18。

【基本概念】

活动：子工程组成的集合，每个子工程即为一个活动。
前驱活动：有向边起点的活动称为终点的前驱活动（只有当一个活动的前驱全部都完成后，这个活动才能进行）。
后继活动：有向边终点的活动称为起点的后继活动。
拓扑排序：将 AOV 网中所有活动排成一个序列，使得每个活动的前驱活动都排在该活动的前面。
拓扑序列：经过拓扑排序后得到的活动序列（一个 AOV 网的拓扑序列不是唯一的）。
关键路径：AOV 网中从源点到汇点的最长路径的长度（一个 AOV 网中的拓扑排序不是唯一的）。

【拓扑排序思想】

选择一个入度为 0 的顶点并输出。
从 AOV 网中删除此顶点及以此顶点为起点的所有关联边。
重复上述两步，直到不存在入度为 0 的顶点为止。
若输出的顶点数小于 AOV 网中的顶点数，则说明 AOV 网中回路，不是一个标准的 AOV 网。

【算法分析】

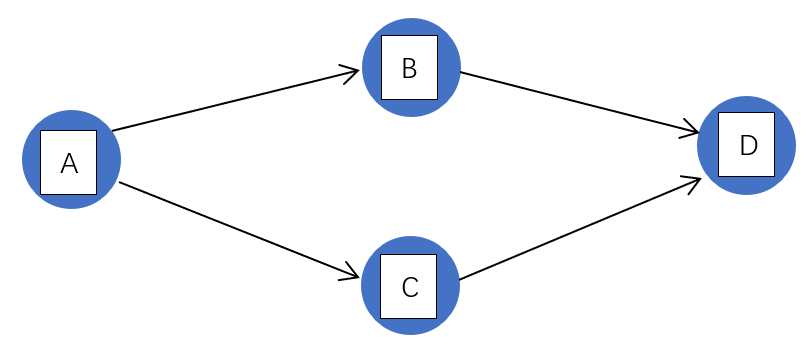
以下图为例

开始时，只有 A 入度为 0，A 入栈。

栈：A

栈顶元素 A 出栈，输出 A，A 的后继节点 B、C 入度减 1（相当于删除 A 的所有关联边）。

栈：空

拓扑序列：A

B、C 入度都为 0，依次将 B、C 入栈

栈：BC（入栈顺序不唯一）

拓扑序列：A

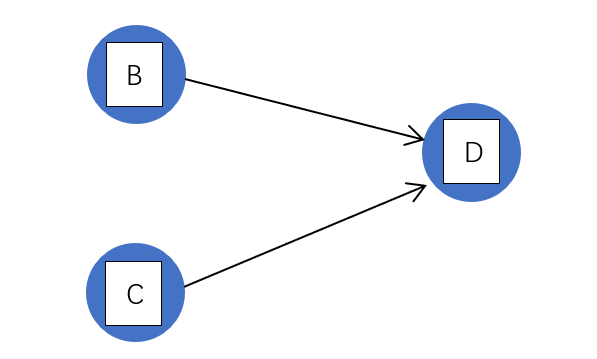
栈顶元素 C 出栈，输出 C，C 的后继结点 D 入度减 1（相当于删除 C 的所有关联边）。

栈：B

拓扑序列：AC

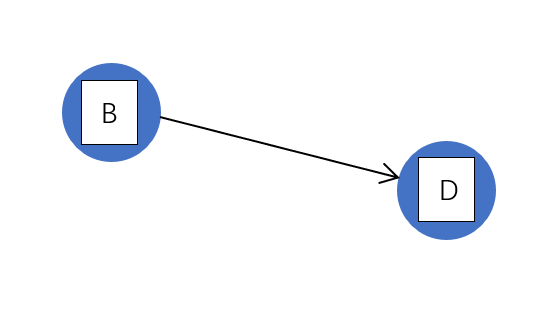
栈顶元素 B 出栈，输出 B，B 的后继结点 D 入度减 1（相当于删除 B 的所有关联边），此时 D 的入度为 0，入栈。

栈：D

拓扑序列：ACB

栈顶元素 D 出栈，输出 D。

栈：空

拓扑序列：ACBD（不唯一）

【AOV 网的判定】

有时，给出一个 n 个点 m 条边的有向图，需要判定图是否是 AOV 网，也即判断图是否可以进行拓扑排序。

一个有向图无法进行拓扑排序时只有一种情况：该有向图中存在环。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<stack>
#include<vector>
#define N 10001
using namespace std;
int n,m;
int in[N];//节点入度
vector<int> G[N];//G[i]表示i节点所指向的所有其他点
bool judgeTopsort()//判断该图是否可拓扑排序
{stack<int> S;int cnt=0;//记录可拆解的点数目for(int i=1;i<=n;i++)//枚举编号从1到n的点if(in[i]==0)//入度为0，入栈S.push(i);while(!S.empty()) {int x=S.top();//取栈顶元素S.pop();cnt++;//可拆点数+1for(int i=0;i<G[x].size();i++){int y=G[x][i];in[y]--;//入度减一if(in[y]==0)//入度为0，出栈S.push(y);}}if(cnt==n)//AOV网点数等于图的点数，不存在环，可进行拓扑排序return true;else//AOV网点数等于图的点数，存在环，不可进行拓扑排序return false;
}
int main()
{while(scanf("%d%d",&n,&m)==2&&n){memset(in,0,sizeof(in));for(int i=1;i<=n;i++)G[i].clear();while(m--) {int x,y;scanf("%d%d",&x,&y);G[x].push_back(y);in[y]++;}printf("%s\n",judgeTopsort()?"YES":"NO");}return 0;
}

【拓扑排序的输出】

1.输出任意一条拓扑排序结果

当给出一 n 个点 m 条边的有向边时，要输出一个可行的点的拓扑序列，此时可根据上述的 AOV 网判定代码，修改后存储路径输出即可。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<stack>
#include<vector>
#define N 10001
using namespace std;
int n,m;
int in[N];//节点入度
int path[N];//存储路径
vector<int> G[N];//G[i]表示i节点所指向的所有其他点
void Topsort()//拓扑排序
{stack<int> S;int cnt=0;//记录可拆解的点数目for(int i=1;i<=n;i++)//枚举编号从1到n的点if(in[i]==0)//入度为0，入栈S.push(i);while(!S.empty()) {int x=S.top();//取栈顶元素S.pop();path[++cnt]=x;//存储可拆点for(int i=0;i<G[x].size();i++){int y=G[x][i];in[y]--;//入度减一if(in[y]==0)//入度为0，出栈S.push(y);}}
}
int main()
{while(scanf("%d%d",&n,&m)==2&&n){memset(in,0,sizeof(in));for(int i=1;i<=n;i++)G[i].clear();while(m--) {int x,y;scanf("%d%d",&x,&y);G[x].push_back(y);in[y]++;}Topsort();for(int i=1;i<=n;i++)printf("%d ",path[i]);printf("\n");}return 0;
}

2.输出按字典序最小的拓扑排序结果

求字典序最小的拓扑序列时，要用优先队列，且是最小值优先的队列，其大致思想是队列 Q 总是将当前在入度为 0 的最小节点优先取出，从而保证了字典序最小。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#include<vector>
#define N 10001
using namespace std;
int n,m;
int in[N];//节点入度
int path[N];//存储路径
vector<int> G[N];//G[i]表示i节点所指向的所有其他点
void Topsort()//拓扑排序
{priority_queue< int,vector<int>,greater<int> > Q;//最小值先出列int cnt=0;//记录可拆解的点数目for(int i=1;i<=n;i++)//枚举编号从1到n的点if(in[i]==0)//入度为0，入列Q.push(i);while(!Q.empty()) {int x=Q.top();//队列首元素Q.pop();path[++cnt]=x;//存储可拆点for(int i=0;i<G[x].size();i++){int y=G[x][i];in[y]--;//入度减一if(in[y]==0)//入度为0，出列Q.push(y);}}
}
int main()
{while(scanf("%d%d",&n,&m)!=EOF&&n){memset(in,0,sizeof(in));for(int i=1;i<=n;i++)G[i].clear();for(int i=1;i<=m;i++){int x,y;scanf("%d%d",&x,&y);G[x].push_back(y);in[y]++;}Topsort();for(int i=1;i<=n;i++)printf("%d ",path[i]);printf("\n");}return 0;
}