算法导论实战（三）（算法导论习题第二十四章）

本文主要是介绍算法导论实战（三）（算法导论习题第二十四章），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

🌈 个人主页：十二月的猫-CSDN博客
🔥 系列专栏： 🏀算法启示录

💪🏻 十二月的寒冬阻挡不了春天的脚步，十二点的黑夜遮蔽不住黎明的曙光

前言

第二十四章

24.1-3

24.1-4

24.2-4

24.3-2

24.3-3

24.3-6

24.3-8

24.3-10

总结

前言

算法导论的知识点学习将持续性更新在算法启示录_十二月的猫的博客-CSDN博客，欢迎大家订阅呀（反正是免费的哦~~）

实战篇也将在专栏上持续更新，主要目的是强化对理论的学习（题目来源：山东大学孔凡玉老师推荐）

第二十四章

24.1-3

问题描述：

假设给定G=(V,E)是一带权重且没有权重为负值的环路的有向图，对于所有的结点𝑣∈𝑉，从源结点s到结点v之间的最短路径中，包含边的条数的最大值为m。请对算法BELLMAN-FORD进行简单修改，可以让其在m+1遍松弛操作之后终止，即使m不是事先知道的一个数值。

问题分析：

如果一个图所有节点到源点s的距离包含的边的条数的最大值为m，那么意味算法在进行m轮松弛后，整个图的所有节点都已经得到最短路径。此时不再需要继续执行m+1轮松弛

问题求解：
在BELLMAN-FORD算法的2-4行的执行记录下松弛前各点的最短路径长度，如果某一次松弛循环结束时所有v.d的值跟本次循环开始时v.d的值相比不发生改变时，此次循环即为第m+1次。

INITALIZE-SINGLE-SOURCE(G,s)
for i=1 to |G.V|-1for each v in G.Vsave v.d to Tfor each edge(u,v) in G.ERELAX(u,v,w)for each v in G.Vif v.d != T[v].dcontinue //没有点的值被更新，说明所有点都取到最短路径，则停止for each edge(u,v) in G.Eif v.d>u.d+w(u,v)return FALSEreturn TRUE

24.1-4

问题描述：
修改Bellman-Ford算法，使其对于所有结点v来说，如果从源结点s都结点v的一条路径上存在权重为负值的环路，则将v.d的值设置为−∞。

问题分析：

贝尔曼福德算法不能够处理存在权重为负值的环路，因为一旦存在则会一直在环路上循环，因为这样的最短路径值会不停缩短。该情况显然是我们不希望发生的，所以我们增加这一个功能来应对存在负值环路的特殊情况。

问题求解：

如果存在负权环路，那么w(u,v)就是无穷小，并且w（s,v)（就是v.d)也是无穷小，于是这个if语句返回值是FLASE。所以只要在if内增加对v.d的修正即可

INITALIZE-SINGLE-SOURCE(G,s)
for i=1 to |G.V|-1for each v in G.Vsave v.d to Tfor each edge(u,v) in G.ERELAX(u,v,w)for each v in G.Vif v.d != T[v].dcontinue //没有点的值被更新，说明所有点都取到最短路径，则停止for each edge(u,v) in G.Eif v.d>u.d+w(u,v)v.d=-∞return FALSEreturn TRUE

24.2-4

问题描述：

给出一个有效的算法来计算一个有向无环图中的点的路径总数。分析你自己的算法。

问题分析：

目前我们手头关于图的知识点只有图的基本算法+最短路径算法+最小生成树，利用这些知识点来思考如何找路径总数。考虑到本题不用考虑有权图，所以我们把眼光转向BFS和DFS两个算法。进一步思考，我们能知道BFS常常用在求解最短路径算法中（BFS特点在于得到的是一棵树，同时每个点都是最短路径的），在这里我们需要求解的是到一个点的所有路径。

假如我们有如下一个图，现在要我们来求解顶点6的路径数

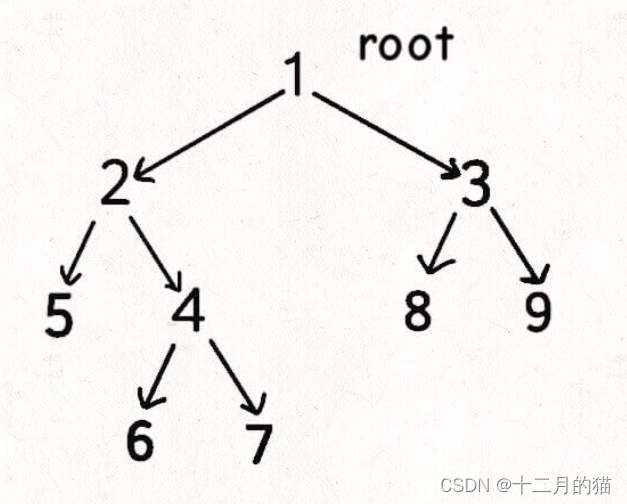
朴素想法：我们最朴素的想法就是从顶点1、2、3、5、4、....、这样的顺序去求解路径数。于是我们可以得到p(1)=1; p(2)+=p(1); p(3)+=p(1); p(5)+=p(2); p(4)+=p(2); 等等。

总的来说，就是从上层到下层计算，下层的路径数：下层路径数+=上层路径数

那什么是下层？什么又是上层呢？

下层：在上层结点撤去后不存在入度结点的点；上层：存在出度给其他顶点

如果可以从上层到下层计算呢？我们就需要对图进行拓扑排序

拓扑排序：是一种对有向图进行排序的算法，其主要目的是确定图中节点的线性顺序，使得在排序后，所有的边都从左到右指向更大的节点。换句话说，拓扑排序可以将图中的节点按照其依赖关系进行排序，使得所有的依赖关系都被满足。

实现拓扑排序的方法有两个：一、计算结点入度+队列方法（通用方法）二、深度搜索（用于无环路的有向图）

本题是有向无环图可以用方法二

问题求解：

一、利用DFS搜索树，将图进行拓扑排序，得到拓扑排序后的图

二、在新的图中，按照拓扑排序的顺序，对每个点u，找其所指向的点v，执行v.paths+=u.paths

PATHS(G)topologically sort the vertices of Gfor each vertex u, taken in topologically sorted orderfor each v ∈ G.Adj[u]v.paths = u.paths + v.pathsreturn the sum of all paths attributes

24.3-2

问题描述：

请举出一个包含负权重的有向图，使得 Dijkstra 算法在其上运行时将产生不正确的结果。为什么在有负权重的情况下，定理 24.6 的证明不能成立呢？

问题分析：

看到对本题的其中一个解答：

大致意思是说：如果存在负权重回路，那么这个RELAX操作是没有意义的，因为RELEX是有限次的，但是通过负权重回路，我们到任何通过这个回路的点的距离都是−∞。于是在RELAX后，u.d并不是（s，u）的最小值，因此不成立

显然上面的证明是没有问题的，但是本题问的是为什么不能有负权重边，而不是负权重回路。所以仅仅有上面的证明是不充分的

问题求解：

Dijkstra算法是贪心贪心算法，也就是说每次都选择贪心策略下的局部最优解，这个解在后续中也不会再修正。那么对于如下的带有负权重的有向图：

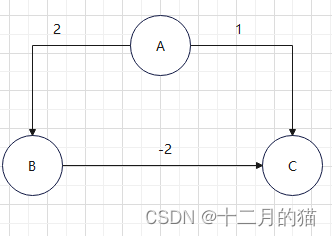
假如源点是A，那么首先选择C此时C值为1；后选择B此时B的值为2，然后又会选择C此时C的值应该要修正为0.但是C的值不会被修正，因此Dijkstra每个点只访问一次（贪心策略）。所以最终C.d=1，但是实际上C到A的最小值为0。因此定理 24.6是不成立的，算法结束后，存在点的d的值不是最短路径值

24.3-3

问题描述：

假定将 Dijkstra 算法的第行改为：

4 ：white（lQl）>1

这种改变将让呻证循环的执行次数从 IVI 次降低到 IVI -1次。这样修改后的算法正确吗？

问题分析：

迪杰斯特拉算法最后得到的结果有两个：一、访问序列s，用来记录对点的访问次序；二、每个点的v.d记录每个点到源点的距离。

所以正确性的证明也将从这两个角度展开：

问题求解：

正确的！

一、假如我们已经得到前面V-1个点的访问序列，那么最后一个点不需要放入，我们也可以只知道最终的访问序列

二、迪杰斯特拉对每个结点只访问一次，且每次都能确定一个点的最短路径，此时程序运行了V-1个循环，访问并确定了V-1个点的最短路径。所以最后一个点进行松弛操作时，它并不能缩短其他点到原点的距离，所以最后一个点的RELAX操作也是无意义的。因此算法是正确的

24.3-6

问题描述：

问题分析：

本题和最短路径问题存在几点不一样：

一、它需要找的是最可靠，也就是值最大的路径，可以认为是最长路径；

二、最短路径算法相连路径段之间的关系是求和，但是通信链路相连路径段求可靠性时之间的关系是求积

问题求解：

一、最长路径。那就把贪婪准则改为选择d最大的点

二、总路径和子路径的关系变为乘。那就修改RELAX准则，从+变为*

三、初始化。源点可靠性为1；其他未搜索到的点初始化为0

INITIALIZE(G,s)for each vertex v ∈ G.Vv.d=0v.π=NULLs.d=1
DIJKSTRA(G,w,s) //s用来记录访问的顺序，是需要返回的值；w边的权重集合S=空集合Q=G.Vwhile(Q <> 空集合）u=EXTRACT-MAX(Q)S=S U {u}for each vertex v∈G.adj[u]RELEX(u,v,w) 
RELAX(u,v,w)if v.d<u.d*w(u,v)v.d=u.d*w(u,v)v.π=u

24.3-8

问题描述：

问题分析：

我第一次看这道题的时候，说实话，连题目都没看懂【emmmmm】。具体原因就在权重函数w：E->{0,1,...,W}这里没看明白。

这个权重函数就表示：边E的权重只能取{1,2,....,W}中的数

再来看看这个WV时间复杂度是哪里来的？要解决这个问题

先让友友们先思考另一个问题：WV含义是什么？

WV含义：图中任意点到源点的距离上限（图中任意点到源点的距离不超过WV）

再来思考一个这个E的时间复杂度含义又是什么？

E是指边，也就是说我需要对边进行E次操作，这不禁让我们想到了松弛操作。

E的复杂度就代表我们要对所有边进行一轮的松弛，每次松弛边本质是更新点的V.d，所以本质就是对点进行了E次的操作

问题求解：

从优化“贪心寻找dist最小点”的操作入手。由于边权≤W≤𝑊，那么一个点的dist值不会超过VW。基于这个条件，我们可以抽象出一个长度为VW的队列数组。每个数组的队列存储着“dist值为该数组序号”的点。然后抽象出一个指针，这个指针指向的队列，是我们贪心取点的队列。由于一个点被取出后，被他更新的点只会被push进该队列或者该队列之后的队列，所以指针只会从左到右扫描一遍数组。

最多扫描一遍数组，复杂度为O(VW）。此外，最多会有E次入队、出队操作，复杂度为O(E)。总时间复杂度为O(VW+E)。

#include <bits/stdc++.h>
#define mp make_pair
using namespace std;
const int N = ..., M = ..., W = ...;
queue<int> qs[N*W];
int head[N], ver[M], edge[M], Next[M], tot = 0;//采用数组模拟邻接链表的方式
void add(int x,int y,int z){ver[++tot] = y, edge[tot] = z, Next[tot] = head[x], head[x] = tot;
}
int d[N], v[N];
int n, m, w;
void dijkstra(int s){memset(d,0x3f,sizeof(d));//初始化为正无穷memset(v,0,sizeof(v));d[s] = 0; qs[0].push(s);for(int k = 0; k<=n*w; k++){while(!qs[k].empty()){int x = qs[k].front(); qs[k].pop();if(v[x]) continue;v[x] = 1;for(int i = head[x]; i; i = Next[i]){int y = ver[i], z = edge[i];if(d[y] > d[x] + z){d[y] = d[x] + z;qs[d[y]].push(y);}}}}
}

24.3-10

问题描述：

假设给定带权重的有向图 G=(V, E), 从源结点s发出的边的权重可以为负值，而其他所有边的权重全部是非负值，同时，图中不包含权重为负值的环路。证明： Dijkstra 算法可以正确计算出从源结点到所有其他结点之间的最短路径。

问题分析：

证明Dijkstra 算法是可行的==证明一个贪心策略是有效的。考虑到Dijkstra 算法本身的贪心策略已经证明结束，所以我们只需要针对其中变化的部分进行特别论证即可

特别部分：从源结点s发出的边的权重可以为负值

利用 Dijkstra 算法取出S，并更新与S相邻的点，将得到多个值不为0的点

于是，该问题可以等效为：多源点且初始值不为0的最短路径问题，并且每个源点都可以适用Dijkstra 算法

因此，整个问题同样可以利用 Dijkstra 算法来求解

问题求解：

首先，Dijkstra的算法思路是：对于任意一个从队列取出来的点x，如果它没有被标记过，那么d[x]一定是源结点s到x的最短路径，然后我们不断地进行贪心扩展，最终可以得到源结点s到每个结点的最短路径。它的本质是一个贪心+BFS算法。
现在，题目中给出的限制是：“只有从源结点s出发的边权重可以为负，且图中无负环”。
源结点s一定是在一开始被取出，更新完之后被丢弃。因为只有源结点s出发的边权重可以为负，所以我们在后面更新由“s以外的其他点”更新“s以外的其他点”时，仍旧是在一个无负边权的图中的更新，所以Dijkstra仍正确。而对于这些点，当他们尝试更新s的时候，因为图中无负环，所以无法更新s。此外，由于无负环，s也不会出现有一个权值为负的子环无限更新自身的情况。综上，Dijkstra基于贪心的性质没有发生改变，每次从队列中取出的一个点更新完其他点被丢弃后，这个点在后面一定不会被更新。所以Dijkstra仍旧可以正确运行。