本文主要是介绍鸢尾花分类和手写数字识别(K近邻),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
鸢尾花分类
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
import pandas as pd
import mglearn# 加载鸢尾花数据集
iris = load_iris()
X_train, X_test, y_train, y_test = train_test_split(iris.data,iris.target,test_size=0.3,random_state=0)# 导入数据集
iris_dataframe = pd.DataFrame(X_train, columns=iris.feature_names)
# 绘制散点矩阵图
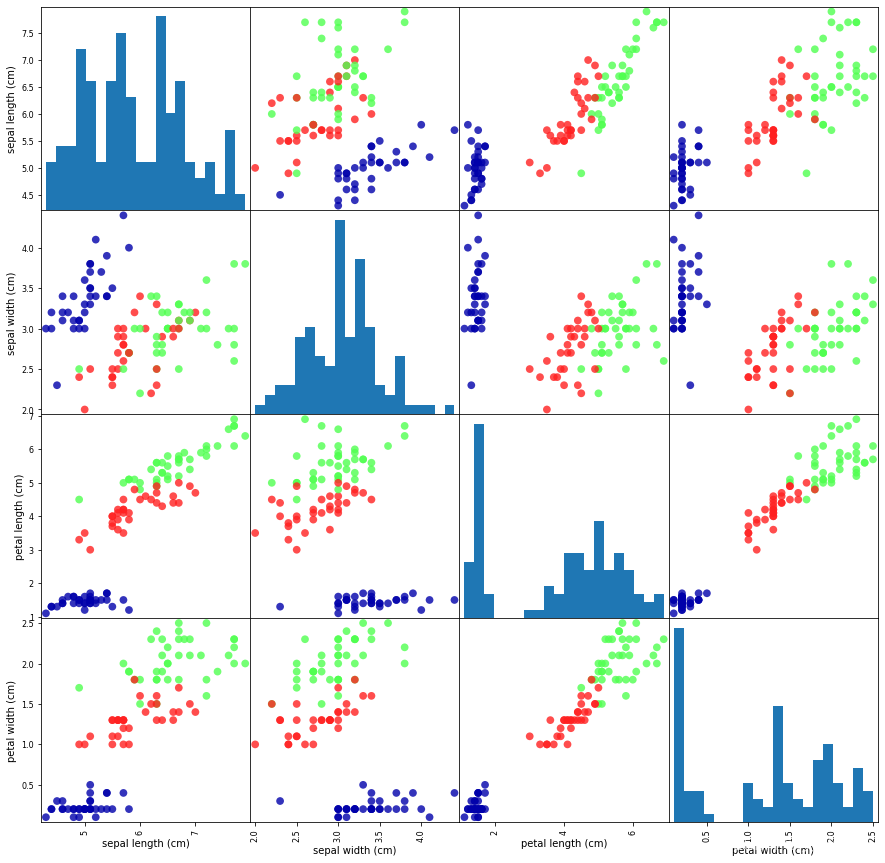
grr = pd.plotting.scatter_matrix(iris_dataframe, # 要绘制散点矩阵图的特征数据c=y_train, # 指定颜色映射的依据figsize=(15, 15),marker='o',hist_kwds={'bins': 20}, # 设置直方图的参数,将直方图分为 20 个区间s=60,alpha=.8,cmap=mglearn.cm3) # 设置颜色映射,这里是使用 mglearn.cm3 颜色映射
from sklearn.neighbors import KNeighborsClassifierknn = KNeighborsClassifier(n_neighbors = 3)
knn.fit(X_train,y_train)
KNeighborsClassifier(n_neighbors=3)
import numpy as np
y_pred = knn.predict(X_test)
print("Test set predictions:\n{}".format(y_pred))
print("Test set score:{:.2f}".format(np.mean(y_pred == y_test)))
Test set predictions:
[2 1 0 2 0 2 0 1 1 1 2 1 1 1 1 0 1 1 0 0 2 1 0 0 2 0 0 1 1 0 2 1 0 2 2 1 02 1 1 2 0 2 0 0]
Test set score:0.98
手写数字识别
import torch
from torch.utils.data import DataLoader
import torchvision.datasets as dsets
import torchvision.transforms as transforms#指定每次训练迭代的样本数量
batch_size = 100
transform = transforms.ToTensor() #将图片转化为PyTorch张量train_dataset = dsets.MNIST(root='./data',train=True,transform=transforms.ToTensor(),download=False)
test_dataset = dsets.MNIST(root='./data',train=False,transform=transforms.ToTensor(),download=False)
#加载数据
train_loader = DataLoader(dataset=train_dataset,batch_size=batch_size,shuffle=True)
test_loader = DataLoader(dataset=test_dataset,batch_size=batch_size,shuffle=True)
print("train data:",train_dataset.data.size())
print("train labels:",train_dataset.targets.size())
print("test data:",test_dataset.data.size())
print("test labels:",test_dataset.targets.size())
train data: torch.Size([60000, 28, 28])
train labels: torch.Size([60000])
test data: torch.Size([10000, 28, 28])
test labels: torch.Size([10000])
import matplotlib.pyplot as plt# 看下第99张图是什么
train = train_loader.dataset.data[98]
plt.imshow(train, cmap=plt.cm.binary)
plt.show()
print(train_loader.dataset.targets[98])

tensor(3)
# 若不进行图像预处理:
import numpy as np
import operator# KNN分类器构建
class KNNClassifier:def __init__(self):self.Xtr = Noneself.ytr = Nonedef fit(self, X_train, y_train):self.Xtr = X_trainself.ytr = y_traindef predict(self, k, dis, X_test):assert dis == 'E' or dis == 'M' # E代表欧氏距离, M代表曼哈顿距离。确保变量dis的值必须是'E'或'M',否则会抛出异常num_test = X_test.shape[0]labellist = []if dis == 'E':for i in range(num_test):distances = np.sqrt(np.sum(((self.Xtr - np.tile(X_test[i], (self.Xtr.shape[0],1))) ** 2), axis=1))nearest_k = np.argsort(distances)[:k]classCount = {self.ytr[i]: 0 for i in nearest_k}for i in nearest_k:classCount[self.ytr[i]] += 1sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)labellist.append(sortedClassCount[0][0])elif dis == 'M':for i in range(num_test):distances = np.sum(np.abs(self.Xtr - np.tile(X_test[i], (self.Xtr.shape[0], 1))), axis=1)nearest_k = np.argsort(distances)[:k]classCount = {self.ytr[i]: 0 for i in nearest_k}for i in nearest_k:classCount[self.ytr[i]] += 1sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)labellist.append(sortedClassCount[0][0])return np.array(labellist)if __name__ == '__main__':X_train = train_loader.dataset.data.numpy() # 转化为numpyX_train = X_train.reshape(X_train.shape[0], 28 * 28)y_train = train_loader.dataset.targets.numpy()X_test = test_loader.dataset.data[:1000].numpy()X_test = X_test.reshape(X_test.shape[0], 28 * 28)y_test = test_loader.dataset.targets[:1000].numpy()num_test = y_test.shape[0]knn = KNNClassifier()knn.fit(X_train, y_train)y_test_pred = knn.predict(5, 'M', X_test)num_correct = np.sum(y_test_pred == y_test)accuracy = float(num_correct) / num_testprint('Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy))
Got 368 / 1000 correct => accuracy: 0.368000
KNN算法在计算距离时对特征的尺度非常敏感。如果图像的尺寸或像素值范围(亮度或颜色深度)不统一,可能会导致距离计算偏向于尺度较大的特征。如:将所有图像归一化到同一尺寸和/或将像素值标准化到同一范围(如0到1),可以确保不同的特征对距离的贡献均衡,从而使KNN分类器更公平、更准确。
KNN算法是基于距离度量(如欧氏距离或曼哈顿距离)来确定每个测试点的“邻居”,因此确保所有特征具有相似的尺度是至关重要的。对于KNN来说,由于它对数据的尺度敏感,选择均值方差归一化通常是更好的选择。
# 代码改进:添加一个均值方差归一化函数def standardize_image(image): #均值方差归一化mean = np.mean(image)std = np.std(image)return (image - mean) / std
# 图像(归一化)
train = train_loader.dataset.data[:1000].numpy()
digit_01 = train[33]
digit_02 = standardize_image(digit_01)
plt.imshow(digit_01, cmap=plt.cm.binary)
plt.show()
plt.imshow(digit_02, cmap=plt.cm.binary)
plt.show()
print(train_loader.dataset.targets[33])
print("Before standardization: mean = {}, std = {}".format(np.mean(digit_01), np.std(digit_01)))
print("After standardization: mean = {}, std = {}".format(np.mean(digit_02), np.std(digit_02)))


tensor(9)
Before standardization: mean = 27.007653061224488, std = 70.88341925375865
After standardization: mean = 5.890979314337566e-17, std = 1.0
虽然归一化前后的图像在视觉上似乎并无明显的差异,但通过打印归一化前后的像素值平均值和标准差可以发现标准化后,数据的平均值为5.890979314337566e-17,接近0(浮点数计算的微小误差,这在数值计算中可以视为0),这是标准化的预期结果,旨在将数据的均值中心化到0;标准差为1.0,确保数据的尺度一致。
if __name__ == '__main__':#训练数据X_train = train_loader.dataset.data.numpy() #转化为numpyX_train = X_train.reshape(X_train.shape[0], 28 * 28)X_train = standardize_image(X_train) #均值方差归一化处理y_train = train_loader.dataset.targets.numpy()#测试数据X_test = test_loader.dataset.data[:1000].numpy()X_test = X_test.reshape(X_test.shape[0], 28 * 28)X_test = standardize_image(X_test)y_test = test_loader.dataset.targets[:1000].numpy()num_test = y_test.shape[0]knn = KNNClassifier()knn.fit(X_train,y_train)# y_test_pred = kNN_classify(5,'M',X_train,y_train,X_test)y_test_pred = knn.predict(5,'M',X_test)num_correct = np.sum(y_test_pred == y_test)accuracy = float(num_correct) / num_testprint('Got %d / %d correct => accuracy: %f' % (num_correct,num_test,accuracy))
Got 950 / 1000 correct => accuracy: 0.950000
这篇关于鸢尾花分类和手写数字识别(K近邻)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





