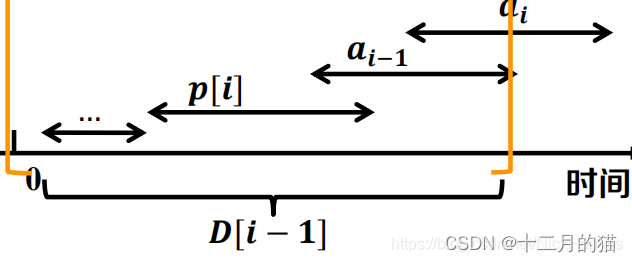算法导论实战（三）（算法导论习题第十六章）

本文主要是介绍算法导论实战（三）（算法导论习题第十六章），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

🌈 个人主页：十二月的猫-CSDN博客
🔥 系列专栏： 🏀算法启示录

💪🏻 十二月的寒冬阻挡不了春天的脚步，十二点的黑夜遮蔽不住黎明的曙光

前言

算法导论的知识点学习将持续性更新在算法启示录_十二月的猫的博客-CSDN博客，欢迎大家订阅呀（反正是免费的哦~~）

实战篇也将在专栏上持续更新，主要目的是强化对理论的学习（题目来源：山东大学孔凡玉老师推荐）

第十六章

16.1-2

假定我们不再一直选择最早结束的活动，而是选择最晚开始的活动，前提仍然是与之前选出的所有活动均兼容。描述如何利用这一方法设计贪心算法，并证明算法会产生最优解。

题解：

思考一个贪心算法的完整流程：

1、证明问题存在最优子结构

2、证明问题存在重叠子问题

3、通过1和2确定问题能够通过动态规划求解

4、思考一个贪心准则

5、证明贪心准则满足局部最优就是全局最优（此外也可以从可行性、安全性两个角度证明）

贪心算法正确性证明：

1、证明问题存在最优子结构

2、证明问题存在重叠子问题

3、证明贪心准则满足局部最优就是全局最优（此外也可以从可行性、安全性两个角度证明）

本题的最优子结构和重叠子问题证明省略~~如果有需要，大家可以去看《算法导论》

本题贪心策略与证明：

贪心准则：选择活动兼容下最晚开始的活动

证明：

贪心算法步骤：

1、选择最晚开始的活动，先让活动进行

2、在剩余兼容活动中再选择最晚开始的活动

3、重复上面的两个步骤，得到最终结果

16.1-4

假定有一组活动，我们需要将它们安排到一些教室，任意活动都可以在任意教室进行。我们希望使用最少的教室完成所有活动。设计一个高效的贪心算法求每个活动应该在哪个教室进行。（这个问题称为区间图着色问题(interval-graphcolor problem)。我们可以构造一个区间图，顶点表示给定的活动，边连接不兼容的活动。要求用最少的颜色对顶点进行着色，使得所有相邻顶点颜色均不相同这与使用最少的教室完成所有活动的问题是对应的。）

题解：

题目分析：

活动选择问题是选择活动序列，要求完成活动数量最多，所以我们对活动是有选择权是否进行的。但是本题是求解完成这些活动所需最少的教室，所以对出现的活动我们都必须选择

本题贪心策略与证明：

贪心准则：选择活动兼容下最晚开始的活动

证明：

贪心算法步骤：

1、在剩余活动中，选择最早结束的活动

2、从最小堆中取出最早空闲的教室。若最小堆为空，则分配一个教室给该活动并将教室加入最小堆中维护(每个教室都记录自己的结束时间）；若是取出的教室结束时间早于活动的开始时间则将该教室继续分配给该活动使用；若是迟于该活动，分配一个教室给该活动并将教室加入最小堆中维护(每个教室都记录自己的结束时间）

3、重复上面的两个步骤，得到最终结果

IntervalGraphColoring(activities)// 按结束时间对活动进行排序sort activities by finishing time in ascending order// 初始化教室列表和当前活动索引classrooms = []current_activity_index = 0// 遍历所有活动while current_activity_index < length(activities):activity = activities[current_activity_index]assigned = false  //目前这个活动是否被分配// 检查当前活动是否可以分配到已存在的教室for classroom in classrooms:if isCompatible(classroom, activity):// 如果兼容，则分配到该教室add activity to classroomassigned = truebreak// 如果没有兼容的教室，则创建新的教室if not assigned:classrooms.append([activity])// 移动到下一个活动current_activity_index += 1return classroomsfunction isCompatible(classroom, activity):for a in classroom:if not (a.finish_time <= activity.start_time or a.start_time >= activity.finish_time):return falsereturn true

16.1-5

考虑活动选择问题的一个变形：每个活动ai除了开始和结束时间外，还有一个值vi。目标不再是求规模最大的兼容活动子集，而是求值之和最大的兼容活动子集。也就是说，选择一个兼容活动子集A,使得值Vi的和最大化。设计一个多项式时间的算法求解此问题。

题解：

题目分析：

本题贪心准则不可以选择结束时间也不可以选择值vi的平均值。或者说本题并不能用贪心算法解决，必须使用动态规划算法。

不能使用贪心的原因：

贪心策略选择的最优解（最大v、v平均值、最早结束、最先开始等贪心策略）都会导致剩下的子问题最优解发生变化，即贪心策略是不安全的

动态规划思路：

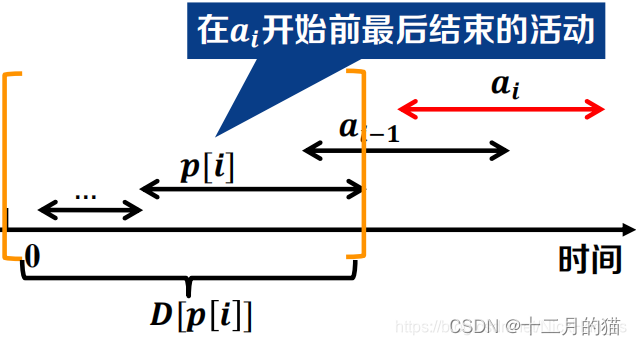
变量定义：D[n]表示在集合{a1,a2,a3,.....,an}中兼容活动的最大权重之和

初始值：D[1]=v1；D[0]=0

动态转移方程：D[n]=max{D[n-1]，D[ p(i) ]+vi}

对于D[n]思考其前一个状态时只能分为两类：a.选择了活动an；b.没有选择活动an

a状态：下一个选择的活动结束时间要在an活动开始时间之前（如下图中不能选择ai-1）

b状态：仅仅不选择an，对下一个选择的活动没有要求

16.2-2

设计动态规划算法求解 0-1 背包问题，要求运行时间为 O(nW), n为商品数量， W是小偷能放进背包的最大商品总重量。

题解：

动态规划思路：

变量定义： $D_m^i$ 表示背包可容纳重量最大为m，从{1,2,...,i}个物品中选择可达到的最大价值

$wi$ 表示第i个物品的重量

$vi$ 表示第i个物品的价值

初始值： $D_m^0$ 、 $D_0^i$ 都为0

转移方程： $D_m^i=max( D_m^{i-1},D_{m-wi}^{i-1}+vi )$

int knapsack01(int n, int W, int weight[], int value[]) {// 初始化一个二维数组 dp 用于存储最优解// dp[i][j] 表示在考虑前 i 个物品，背包容量为 j 时的最大价值int dp[n + 1][W + 1];// 初始化边界条件for (int w = 0; w <= W; ++w) {dp[0][w] = 0; // 没有物品时，最大价值为0}for (int i = 0; w <= W; ++w) {dp[i][0] = 0; // 背包容量为0时，最大价值为 0}for (int i = 1; i <= n; ++i) {for (int w = 0; w <= W; ++w) {if (weight[i] > w) {// 当前物品重量大于背包容量，无法装入，继承前一个状态的最优解dp[i][w] = dp[i-1][w];} else {// 当前物品可以装入背包// 要么选择装入当前物品，价值为 value[i] 加上剩余容量 w-weight[i] 时的最优解// 要么选择不装入当前物品，继承前一个状态的最优解dp[i][w] = max(dp[i-1][w], dp[i-1][w-weight[i]] + value[i]);}}}// 返回最优解，即 dp[n][W]return dp[n][W];
}

16.2-3

假定在 0-1 背包问题中，商品的重量递增序与价值递减序完全一样。设计一个高效算法求此背包问题的变形的最优解，证明你的算法是正确的。

题解：

本题显然可以使用贪心算法来求解

贪心策略为：每次都选择剩余物品中最轻的物品

贪心算法正确性证明（忽略最优子结构、重叠子问题的证明）：

假设有一个子问题P，其最优解为S，即物品集S为价值最大物品集。aj为该物品集中最轻的物品（也就是价值最大的物品），am为子问题P中所有物品中最轻的物品（也就是所有物品中价值最大的物品）。此时将aj替换为am，由于w(am)<=w(aj)，所以背包重量一定不会超；同时v(am)>=v(aj)，所以新物品集S‘>=S。因此am必然也在其中一个全局最优解中，即该贪心策略下的局部最优解就是全局最优解，证毕！

16.2-4

Gekko 教授一直梦想用直排轮滑的方式横穿北达科他州。他计划沿U.s. 2 号高速公路横穿，这条高速公路从明尼苏达州东部边境的大福克斯市到靠近蒙大拿州西部边境的威利斯顿市。教授计划带两公升水，在喝光水之前能滑行m英里（由千北达科他州地势相对平坦，教授无需担心在上坡路段喝水速度比平地或下坡路段快）。教授从大福克斯市出发时带整整两公升水。他携带的北达科他州官方地图显示了 U.s. 2 号公路上所有可以补充水的地点，以及这些地点间的距离。求解加水次数最少的补充水方法

题解：

本题显然能够用贪心算法求解，不需要使用动态规划方法去遍历所有问题

贪心策略为：

1、从出发点/加水点开始

2、以该点向后取m英里的线段
3、选择线段内离线段结束点最近的加水点

4、在该加水点加水，重复123步骤

证明贪心算法正确性：

最优子结构：从后面任意补充水的地点将问题分为左右两个子问题，其中每个子问题都应该是最优解，否则利用cut-and-paste能够证明其存在矛盾

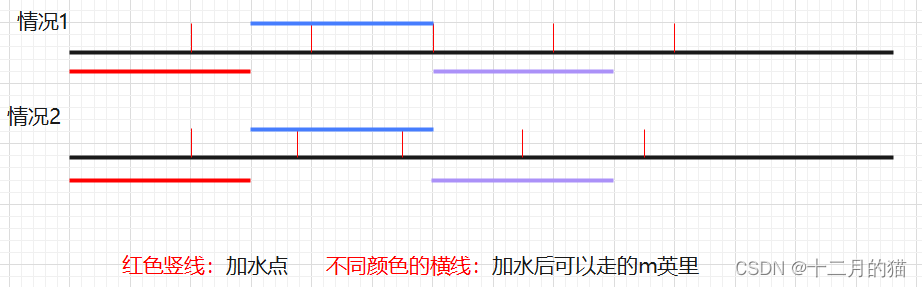
重叠子问题：从后面任意补充水的地点将问题分为左右两个子问题。如果两个子问题有每次补充水后达到的m英里长度的线段内的补充水地点个数相同（也可以不相同，仅仅是保证到终点前的每一段，两者线段中都至少有一个补充点即可），那么这两个子问题便是重叠的。

一个疑问：左右两段构成的两个子问题，补充水分的地点肯定不完全一致，那为什么是重叠子问题？

解释：如上图所示，虽然两个情况的加水点不一样，但是本质上两个问题（因为两个情况的加水可走线段内的补充点个数都是相同的

局部最优就是全局最优：假设P为原问题，S为原问题下的最短补充水序列{s1,s2,....,sn}。假设第一次滑行线段内离结束点最近的补水点为sm，那么sm到m的距离一定小于等于s1到m的距离。于是我们将s1替换为sm，此时sm构成的下一个长度为m的线段一定比s1构成的更加向后（至少一样），所以必然包括s2点。因此sm必然在一个最短补水序列中，即局部最优解一定在其中一个全局最优解中

16.2-5

设计一个高效算法，对实数线上给定的一个点集{x1,x2, …,xn｝，求一个单位长度闭区间的集合，包含所有给定的点，并要求此集合最小。证明你的算法是正确的。

题解：

贪心策略：

1) 从点集中取最小的点；
2) 取以该点为左起点的单位闭区间，然后从点集中去掉包含在该单位闭区间的所有点；
3) 重复1）-2）,直到所有的点处理完毕；那么2）得到的单位闭区间集合A即为所求；

证明：
I) 从2)中看到，点集中的任意点必定包含在A的某一单位闭区间中，即2）得到的单位闭区间集合A是的问题的一个解；
II) 假设B是一最优解，那么B中必定有一个单位闭区间包含点集的最小点；
由于 “包含该最小点的单位闭区间能包含的点集中的点” 总是 “以该点为左起点的单位闭区间能包含的点集中的点” 的子集；
所以用以最小点为左起点的单位闭区间代替B中包含该最小点的单位闭区间, 得到的新的解不会比B更差，即A也是最优解；

16.2-6

设计算法，在 O(n)时间内求解分数背包问题。

题解：

题目分析：本题是典型的一个利用分治思想解决可以提高运行效率的问题

一般解法：最朴素的解法运行效率为O(nlgn)

对所有物品按照价值大小进行排序，花费O(nlgn)
假设加入物品i，若sum(w)+wi<w，则加入物品；否则不加入
重复步骤2，直到遍历完所有物品一遍才停止，花费O(n)

思考：

1、一般解法是否还能够提高运行效率？

2、一般解法耗费运行效率的点在于哪里？

显然，最耗费资源的地方在于对所有物品按价值进行排序，那么这是必要的吗？

这个排序所带来的就是我们能够按照价值从大到小依次放入包中，例如{a1，a2,...,ak}，但是我们并不需要严格按照这个次序放入包中，我们也可以{a3,a4,a9,....,a1}等等各种序列，只要仍然是这些物品即可。所以，这个排序是非必要的，必要的是找出这些物品

找满足条件的物品集——>划分物品集——>中位数划分法

到这里，我们就确定中位数划分法来找背包物品集。下面就来具体看看算法思想~~

算法思路：

Step1：首先利用线性查找算法找出物品单位价值的中位数m；

Step2：利用中位数m对所有物品进行划分成三个集合 WG= {Vi/Wi>m} WE = {Vi/Wi=m} WL = {Vi/Wi<m},计算 WG、WE、WL集合中物品的总重量；

Step3：比较WG和W。

若 WG>W，尽可能多地放WG中的物品，从Step1开始继续分解WG（特殊情况WG=W，把WG物品全放进去）；
若 WG<W，则把WG中的物品全部放入背包，并且尽可能多地放WE中的物品（特殊情况WG+WE=W，把WG、WE物品全放进去）；
若 WG+WE<W,则把WG+WE的物品全部放入，从Step1开始继续分解WL。

分析算法：

核心：每次都至少缩小一半的分解范围

T(n) = T(n/2)+n 即T(n)每次缩小一半的计算量，由主方法可知T(n) = n.