本文主要是介绍【数据结构】排序(直接插入、折半插入、希尔排序、快排、冒泡、选择、堆排序、归并排序、基数排序),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
- 排序
- 一、插入排序
- 1.直接插入排序
- 2.折半插入排序
- 3.希尔排序
- 二、交换排序
- 1.快速排序
- 2.冒泡排序
- 三、选择排序
- 1. 简单选择排序
- 2. 堆排序
- 3. 树排序
- 四、归并排序(2-路归并排序)
- 五、基数排序
- 1. 桶排序(适合元素关键字值集合并不大)
- 2. 基数排序
- 基数排序的基本原理
- 基数排序的实现步骤
- 基数排序的代码实现
排序
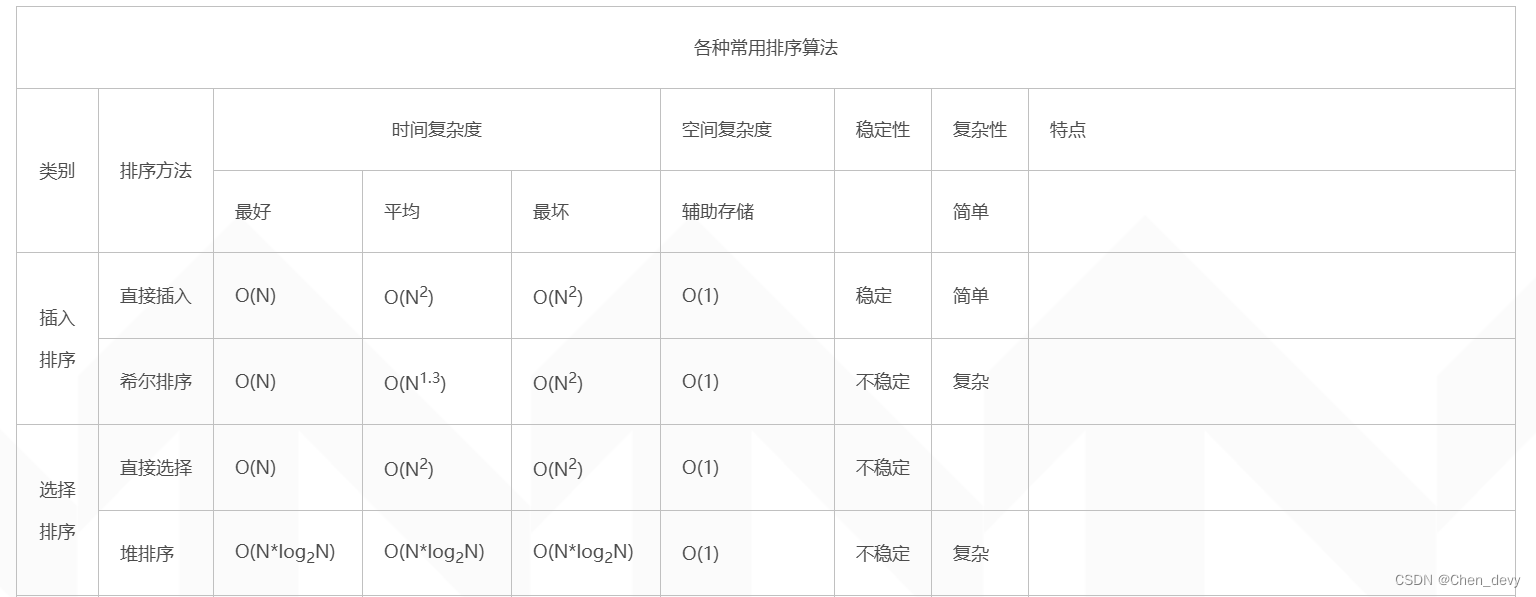
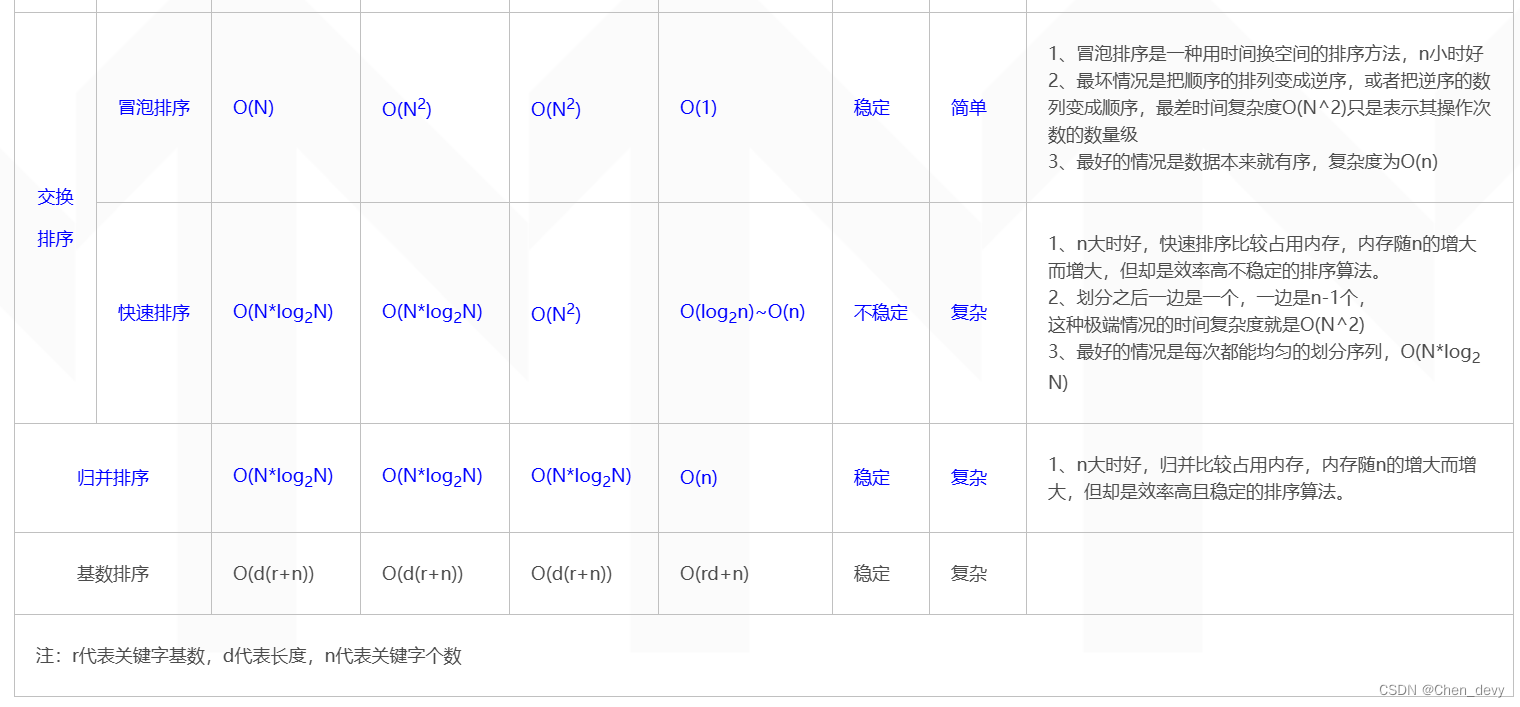
图片取自博客园 链接: 各种排序算法时间复杂度
1. 排序定义:排序定义——将一个数据元素(或记录)的任意序列,重新排列成一个按关键字有序的序列叫排序(sort)。
按照主关键字排序,排序结果唯一;按照次关键字排序,排序结果可能不唯一。
2. 排序分类:
1.按排序记录所在位置分类:
(1)内部排序:待排序记录存放在内存中;
(2)外部排序:排序过程中需要对外存进行访问的排序;
2.按排序依据分类:
3. 排序所需工作量

4.排序的稳定性
待排序数列中如果有关键字相等的记录,经过某一算法排序后,关键字相等的记录其先后次序始终不变,则这种算法成为稳定的排序算法,具有稳定性。否则不稳定,不具有稳定性。
一、插入排序
插入排序:每次将一个待排序的记录,按关键字的大小插入到已排好序的子序列中的适当位置,直到全部记录插入完毕为止
数据元素类型以及顺序存储结构结构体定义如下:
//数据元素类型
typedef struct{KeyType key; //关键字域//...; //后面就是其它关键字
}ElemType;//数据元素类型//表的顺序存储结构
typedef struct{ElemType r[MAXSIZE+1]; //其中r[0]项为 哨兵项 以便交换的时候 暂存数据int length;//表的长度
}SqList; //顺序存储结构
1.直接插入排序
直接插入排序,待排序的数据用数组和链表存放均可
算法评价:稳定!
时间复杂度: O ( n 2 ) O(n^2) O(n2)
- 最好情况: O ( n ) O(n) O(n)
最好情况:n-1次数据比较,0次数据移动。待排序的数据已经有序。- 平均情况: O ( n 2 ) O(n^2) O(n2)
- 最坏情况: O ( n 2 ) O(n^2) O(n2)
空间复杂度:一个额外的辅助空间 O ( 1 ) O(1) O(1)

//数据元素类型
typedef struct{KeyType key; //关键字域//后面就是其它关键字
}ElemType;//数据元素类型//表的顺序存储结构
typedef struct{ElemType r[MAXSIZE+1]; //其中r[0]项为 哨兵项 以便交换的时候 暂存数据int length;//表的长度
}SqList; //顺序存储结构
算法实现:
void InsertSort(SqList L){int i,j;for(i=2;i<=length;i++){//从第二个到第n个记录依次插入if(L.r[i].key<L.r[i-1].key){L.r[0] = L.r[i];for(j=i-1;L.r[0].key<L.r[j].key;i--){//若r[0]<r[j],则r[j]后移L.r[j+1]=L.r[j];}L.r[j+1]=L.r[0];//将r[0]移至在r[j+1]}}
}2.折半插入排序
待排序的数据元素必须存放于数组
算法评价: 稳定!
时间复杂度: T ( n ) = O ( n 2 ) T(n)=O(n^2) T(n)=O(n2)
空间复杂度: S ( n ) = O ( 1 ) S (n)=O(1) S(n)=O(1)
与直接插入排序相比,查找插入位置方法不同,记录移动次数不变
算法实现:
void BinSrot(SqList &L){int i,j,high,low,mid;for(int i=2;i<=L.length;i++){L.r[0]=L.r[i];low=1;high=i-1;while(low<=high){//折半查找mid=(low+high)/2;if(L.r[0].key<L.r[mid].key)high=mid-1;else low=mid+1;}for(j=i-1;j>=low;j--){L.r[j+1]=L.r[j]; //后移}L.r[low]=L.r[0]; //插入}
}
//(high<low ,查找结束,插入位置为low 或high+1 )
二分插入排序减少了关键字的比较次数,但数据元素的移动次数不变,其时间复杂度与直接插入排序相同。
待排序的数据元素必须存放于数组
算法评价:
时间复杂度: T ( n ) = O ( n 2 ) T(n)=O(n^2) T(n)=O(n2)
空间复杂度: S ( n ) = O ( 1 ) S (n)=O(1) S(n)=O(1)
3.希尔排序
算法评价:不稳定!
时间复杂度: O ( n l o g 2 n ) O(nlog^2n) O(nlog2n)
- 最好情况: O ( n l o g n ) O(nlog~n) O(nlog n)
- 平均情况: O ( n l o g 2 n ) O(nlog^2n) O(nlog2n)
- 最差情况: O ( n l o g 2 n ) O(nlog^2n) O(nlog2n)
空间复杂度: O ( 1 ) O(1) O(1)

先将整个待排序记录分割成若干个子序列分别进行直接插入排序,待整个序列中的记录基本有序时,再对全体记录进行一次直接插入排序。
对待排记录先作“宏观”调整,再作“微观”调整。
增量序列可以有各种取法,但应注意:应使增量序列中的值没有除1的之外的公因子,并且最后一个增量值必须等于1。
希尔排序原理:
//希尔排序void ShellInsert ( SqList &L, int dk ) {//直接插入排序for ( i=dk+1; i<=n; ++i )//if ( L.r[i].key< L.r[i-dk].key) {L.r[0] = L.r[i]; // 暂存在R[0]for (j=i-dk; j>0&&(L.r[0].key<L.r[j].key); j-=dk)L.r[j+dk] = L.r[j]; // 记录后移,查找插入位置L.r[j+dk] = L.r[0]; // 插入} // if
} // ShellInsertvoid ShellSort (SqList &L, int dlta[], int t)
{ // 增量为dlta[]的希尔排序for (k=0; k<t; ++t) //增量ShellInsert(L, dlta[k]);//一趟增量为dlta[k]的插入排序//增量//dlta[k] 怎么取?} // ShellSort二、交换排序
交换排序:两两比较待排序记录的关键值,交换不满足顺序要求的记录,直到全部满足顺序要求为止
//数据元素类型
typedef struct{KeyType key; //关键字域//后面就是其它关键字
}ElemType;//数据元素类型//表的顺序存储结构
typedef struct{ElemType r[MAXSIZE+1]; //其中r[0]项为 哨兵项 以便交换的时候 暂存数据int length;//表的长度
}SqList; //顺序存储结构
1.快速排序
递归!!!
算法评价:不稳定排序
时间复杂度: O ( n l o g 2 n ) O(nlog_{2}n) O(nlog2n)
- 最好情况: O ( n l o g 2 n ) O(nlog_{2}n) O(nlog2n)
- 平均情况: O ( n l o g 2 n ) O(nlog_{2}n) O(nlog2n)
- 最差情况: O ( n 2 ) O(n^2) O(n2)
空间复杂度: O ( l o g 2 n ) − O ( n ) O(log_{2}n)-O(n) O(log2n)−O(n) 认为是 O ( l o g 2 n ) O(log_{2}n) O(log2n)
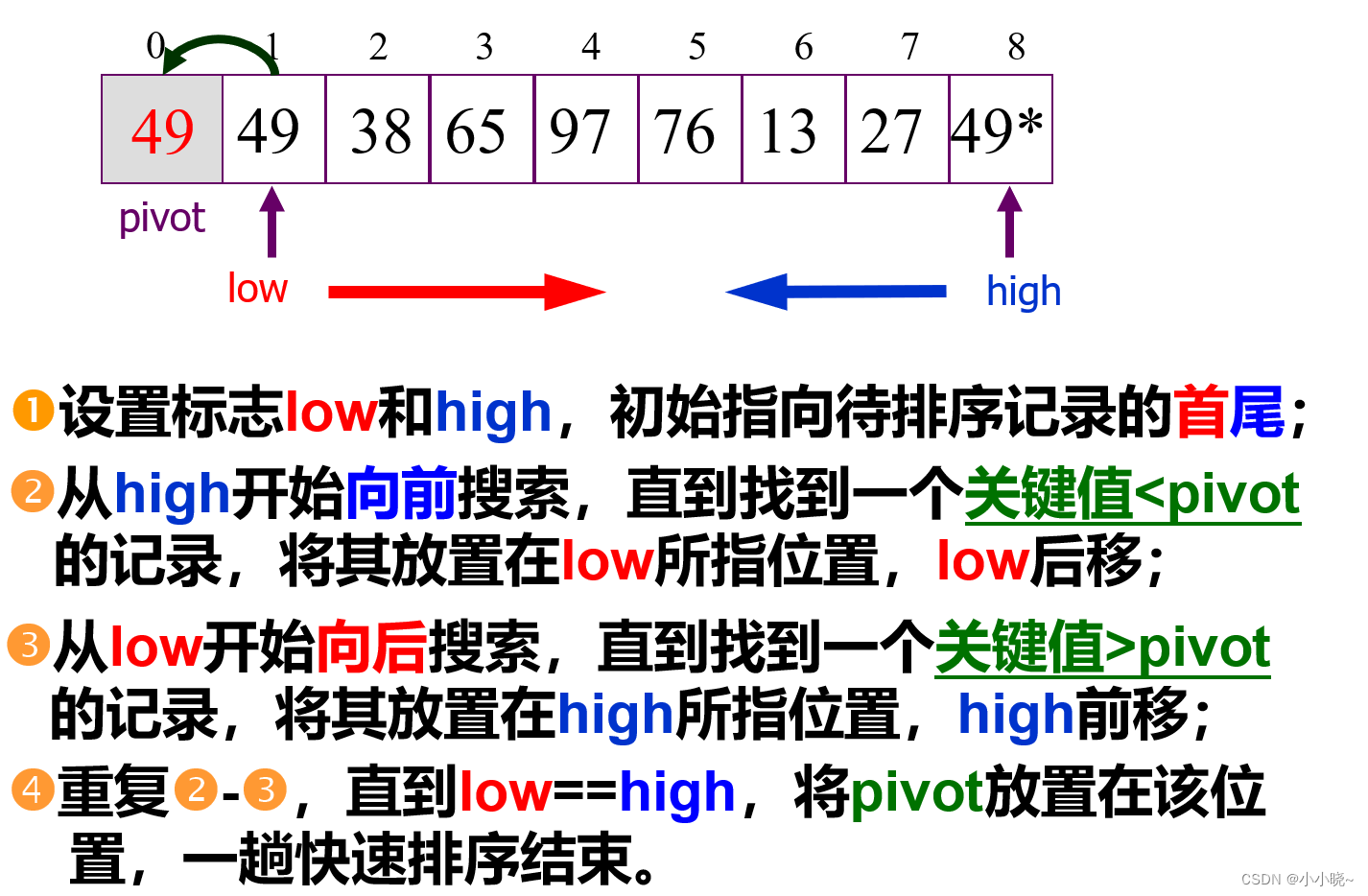
- 原理:
在待排序记录中任取一个记录(通常为第一个记录) , 作为枢轴(pivot)(基准),将其它记录分为两个子序列:
- 所有键值比它(枢轴)小的安置在一部分。
- 所有键值比它(枢轴)大的安置在另一部分。
(与基准相同的数据元素的处理:放在基准的右侧) - 把该数据元素放在这两部分的中间,这也是该数据元素排序后的最终位置这个过程称为一趟快速排序。
基准的选取:第一个数据元素、最后一个数据元素、中间位置的数据元素
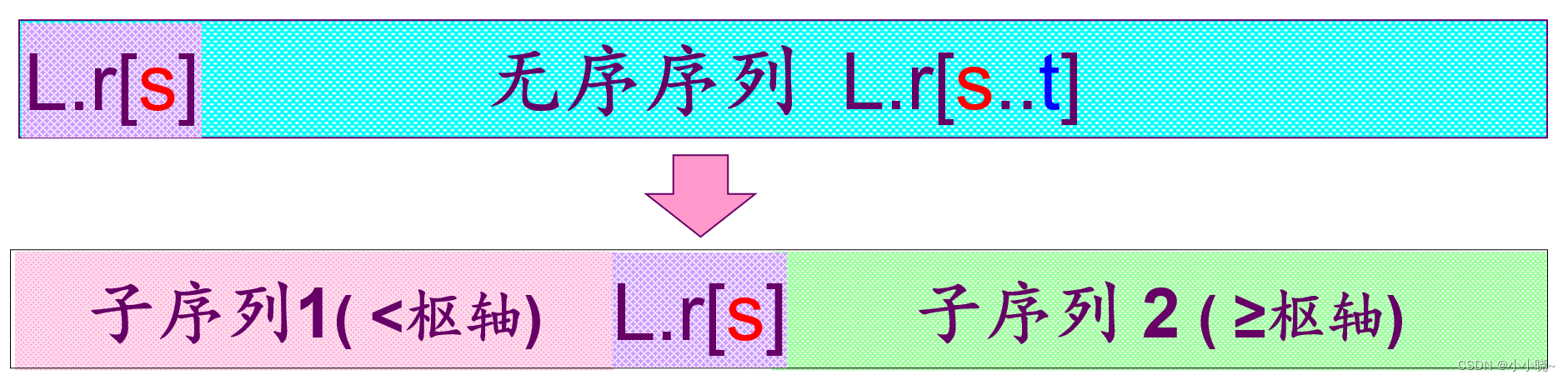
快速排序实现过程:
快速排序每趟的算法:
int Partition(SqList &L,int low,int high){keyType pivotkey;//数据类型 上述定义的包含关键字的数据类型L.r[0]=L.r[low];//保护 枢轴pivotkey=L.r[row].key;while(low<high){while(L.r[high].key>=pivotkey&&low<high) high--;//一直移动 直到if(low<high){L.r[low]=L.r[high];low++;}while(L.r[low].key<=pivotkey&&low<high) low++; //一直移动 直到if(low<high){L.r[high]=L.r[low];high--;}}L.r[low]=L.r[0];return low;
}
算法分析:
快速排序:(小规模数据 不适合快排)
void QuickSort(SqList &L,int low,int high){int pivotloc;if(low<high){pivotloc=Partition(L,low,high);QuickSort(L,low,pivotloc-1);QuickSort(L,pivotloc+1,high);}
}int Partition(SqList &L,int low,int high){keyType pivotkey;//数据类型 上述定义的包含关键字的数据类型L.r[0]=L.r[low];//保护 枢轴pivotkey=L.r[row].key;while(low<high){while(L.r[high].key>=pivotkey&&low<high) high--;//一直移动 直到if(low<high){L.r[low]=L.r[high];low++;}while(L.r[low].key<=pivotkey&&low<high) low++; //一直移动 直到if(low<high){L.r[high]=L.r[low];high--;}}L.r[low]=L.r[0];return low;
}递归!!!
算法评价:不稳定排序
时间复杂度: O ( n l o g 2 n ) O(nlog_{2}n) O(nlog2n)
- 最好情况: O ( n l o g 2 n ) O(nlog_{2}n) O(nlog2n)
- 平均情况: O ( n l o g 2 n ) O(nlog_{2}n) O(nlog2n)
- 最差情况: O ( n 2 ) O(n^2) O(n2)
空间复杂度: O ( l o g 2 n ) − O ( n ) O(log_{2}n)-O(n) O(log2n)−O(n)
-
最差情况

-
快速排序的最好情况:每次总是选到中间值作枢轴
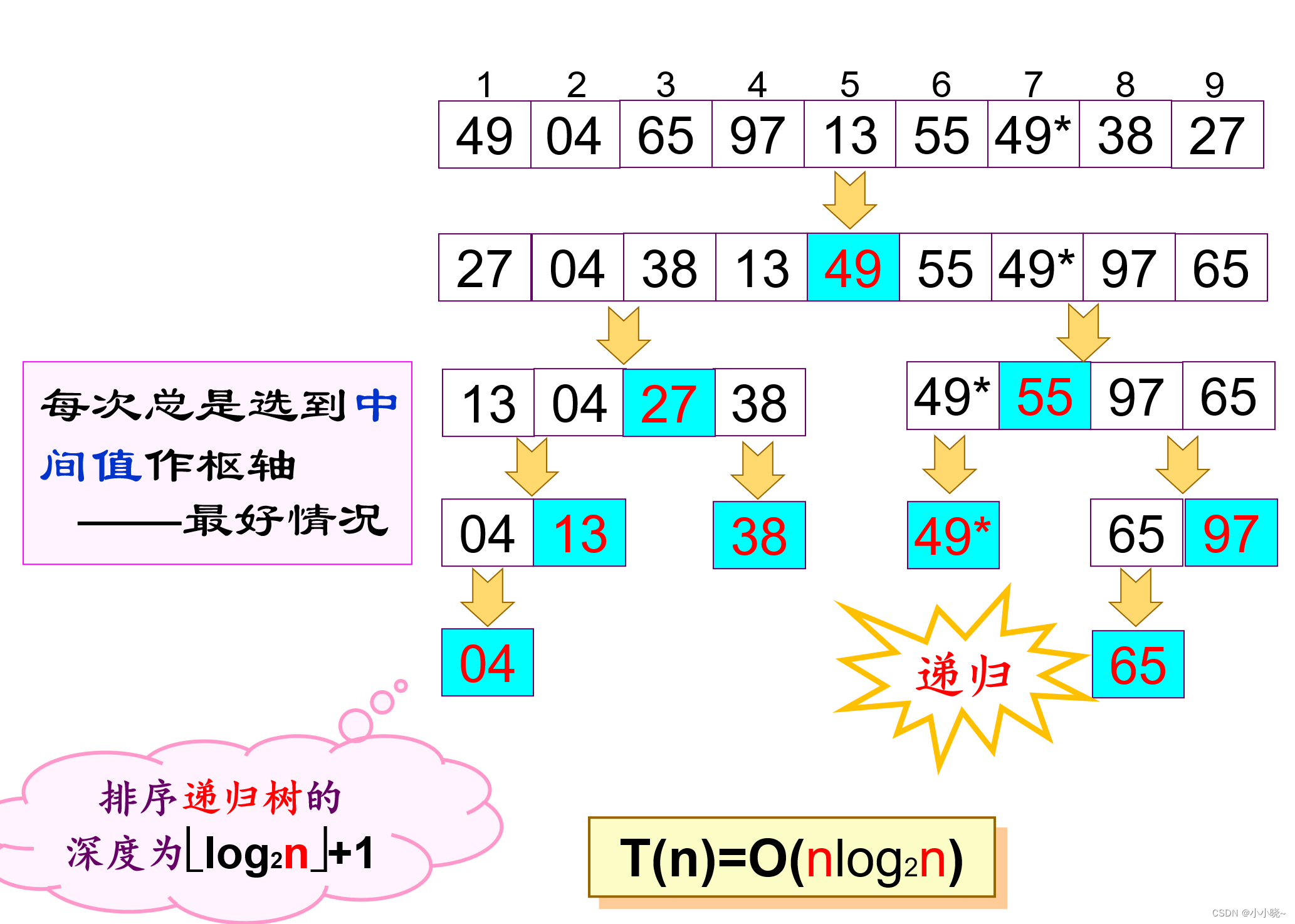
-
空间复杂度: O ( l o g 2 n ) − O ( n ) O(log_{2}n)-O(n) O(log2n)−O(n)
原因 使用递归的方法进行排序,需要使用到栈空间

图片来源 :快速排序时间复杂度和空间复杂度
2.冒泡排序
算法评价:稳定!
时间复杂度: O ( n 2 ) O(n^2) O(n2)
- 最好情况: O ( n ) O(n) O(n)
- 平均情况: O ( n 2 ) O(n^2) O(n2)
- 最差情况: O ( n 2 ) O(n^2) O(n2)
空间复杂度: O ( 1 ) O(1) O(1)
- 将待排序的数据元素的关键字顺次两两比较,若为逆序则将两个数据元素交换。
- 将序列照此方法从头到尾处理一遍称作一趟冒泡排序,它将关键字值最大的数据元素交换到排序的最终位置。
- 若某一趟冒泡排序没发生任何数据元素的交换,则排序过程结束。
- 对含
n个记录的文件排序最多需要n-1趟冒泡排序。
void BubbleSort( SqList &L){ int m, j, flag=1;//用于判断是否已经排好序 m=L.length-1;while((m>0)&&(flag= =1)){ flag=0;for(j=1;j<=m;j++) if(L.r[j].key>L.r[j+1].key){//冒泡排序是稳定的排序方法 没有等号 flag=1;//此次过程交换了 标记一下L.r[0]=L.r[j]; L.r[j]=L.r[j+1]; L.r[j+1]=L.r[0];}m--;}
}时间复杂度: O ( n 2 ) O(n^2) O(n2)
- 最好情况: O ( n ) O(n) O(n)
- 平均情况: O ( n 2 ) O(n^2) O(n2)
- 最差情况: O ( n 2 ) O(n^2) O(n2)
空间复杂度: O ( 1 ) O(1) O(1)
最好情况:n个数据元素,1趟冒泡排序,0次数据移动,n-1次比较。(初始的待排序序列恰好是有序)
最坏情况:n个数据元素, n-1趟冒泡排序。(初始的待排序序列恰好是逆序)
三、选择排序
选择排序:每次从待排序记录中选出关键字最小的记录,顺序放在已排序的记录序列的后面,直到全部排完为止
1. 简单选择排序
算法评价:不稳定!!!
时间复杂度: O ( n 2 ) O(n^2) O(n2)
- 最好情况: O ( n 2 ) O(n^2) O(n2)
- 平均复杂度: O ( n 2 ) O(n^2) O(n2)
- 最差情况: O ( n 2 ) O(n^2) O(n2)
空间复杂度: O ( 1 ) O(1) O(1)
!!!情况最好比较n-1次 无需交换,情况最差不是逆序
不论输入的待排序的数据是什么顺序,每一趟简单选择排序的比较次数不变,总的比较次数为:(n-1)+(n-2)+…+2+1=n(n-1)/2次
最好情况:第一趟找到的最小的恰好在第一个位置,不发生数据交换,…, 每一趟找到的最小的数据都不要交换,输入的待排序的数据恰好有序,总的数据移动次数为0次。
最坏情况:第一趟找到的最小的要交换到第一个位置,数据移动3次,…, 每一趟找到的最小的都要交换,数据移动 3次。总共n-1趟,总的数据移动次数3(n-1)次。
数据移动指的是交换 每次交换数据就要移动三次
适用于待排序元素较少的情况
算法实现:
void SelectSort( SqList &L)
{ int i, j, k;for(i=1;i<L.length;i++) { k=i; for(j=i+1;j<=L.length;j++)//查找最小的if(L.r[j].key<L.r[k].key) k=j;//if(i!=k){ L.r[0].key=L.r[i]; L.r[i]=r[k]; L.r[k]=L.r[0].key; }}
}
2. 堆排序
算法评价:不稳定
时间复杂度: O ( n l o g 2 n ) O(nlog_{2}n) O(nlog2n)
- 最好情况: O ( n l o g 2 n ) O(nlog_{2}n) O(nlog2n)
- 平均情况: O ( n l o g 2 n ) O(nlog_{2}n) O(nlog2n)
- 最坏情况: O ( n l o g 2 n ) O(nlog_{2}n) O(nlog2n)
空间复杂度: O ( 1 ) O(1) O(1)
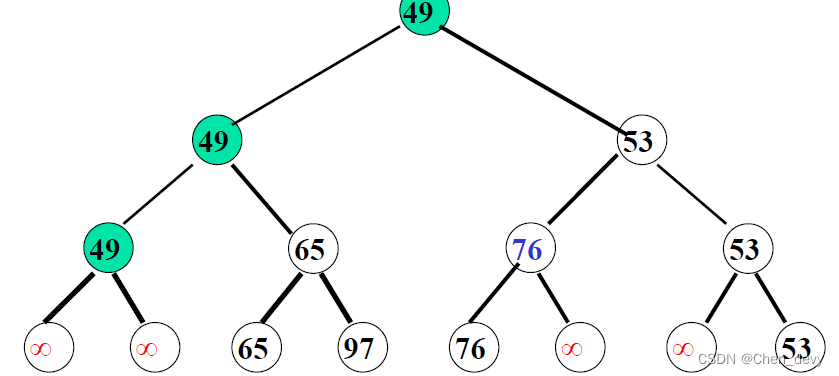
可将堆序列看成完全二叉树的顺序存储,堆顶元素(完全二叉树的根)必为序列中n个元素的最小值或最大值

初建堆(大顶堆):
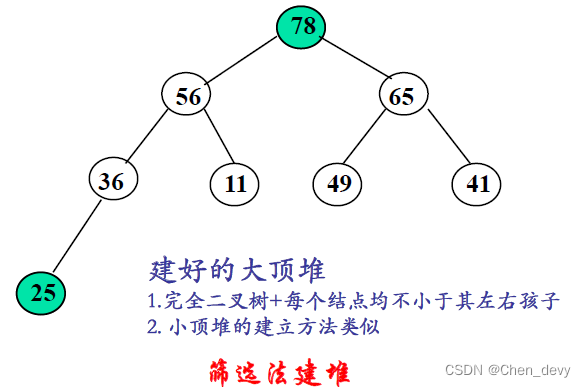
第一趟排序:
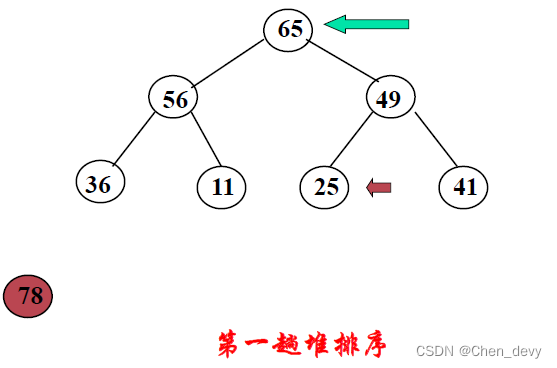
第二趟排序:

第三趟排序:
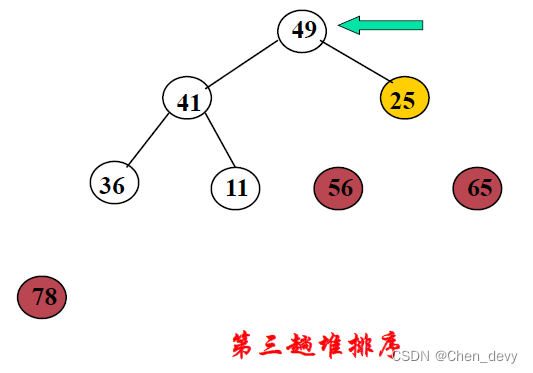
第四趟排序:
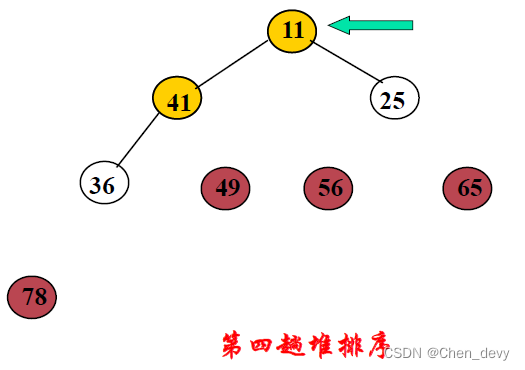
第五趟排序:
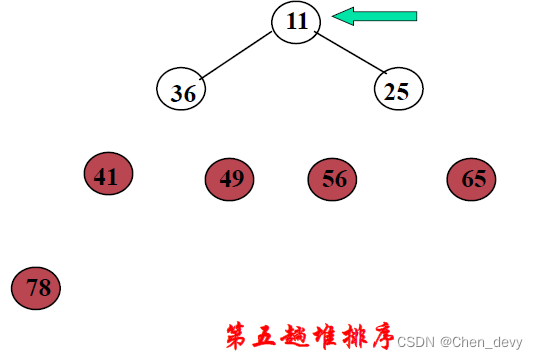
第六趟排序:
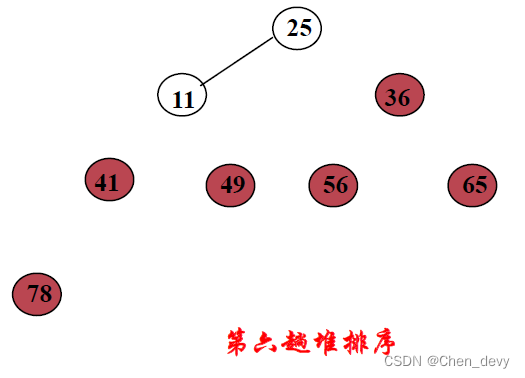
第七趟排序:
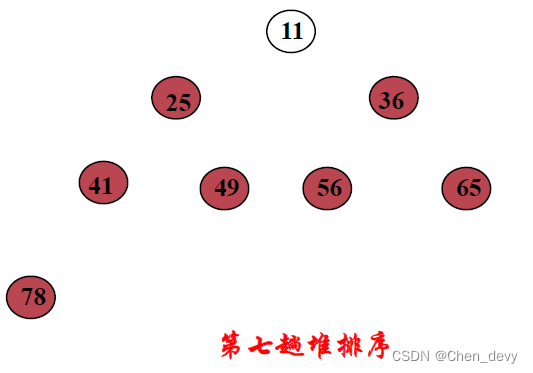
堆排序 完全排好序: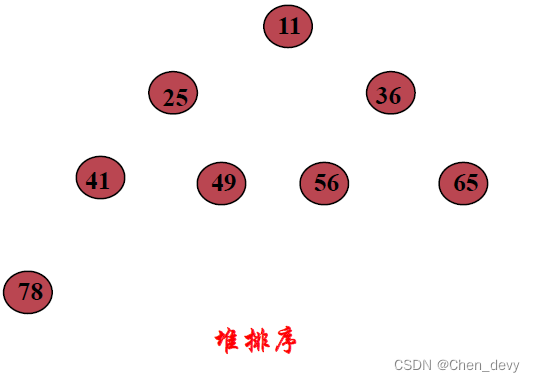

void HeapSort(SqList &L){ int i,j,k;for (i=L.Length/2;i>0;--i)//筛选法建堆,从n/2处开始调整HeapAdjust(L,i,L.Length); //调整以i为根结点的子树为一个大顶堆for(i=L.Length;i>1;--i)//n-1趟堆排序,当前大顶堆中的数据元素i个,L.r[1]中是i个数据元素中的最大值{ L.r[0]=L.r[i];L.r[i]=L.r[1];L.r[1]=L.r[0];//将堆中最大的数据元素L.r[1]交换到第i个位置,也是它最终排序后的位置HeapAdjust(L,1,i-1);////堆中数据元素个数为i-1,将i-1个数据元素重新调整为大顶堆}
}
//函数HeapAdjust(L,i,L.Length)-调整以i为根结点的子树为一个大顶堆void HeapAdjust(SqList &L,int s,int m)
//调整以s为根结点的子树为一个大顶堆,堆中最大的数据元素编号为m,且以s为根的子树中除根结点s外,均满足大顶堆的定义
{ int j;L.r[0]=L.r[s]; //记录下 根节点的信息for(j=2*s, j<=m; j=j*2){ if(j<m && L.r[j].key< L.r[j+1].key) ++j;//j为左、右孩子中最大的那个if(L.r[0].key>=L.r[j].key) break; L.r[s]=L.r[j];s=j;}L.r[s]=L.r[0];//
}3. 树排序
树排序将时间复杂度降为 O ( n l o g 2 n ) O(nlog_{2}n) O(nlog2n),但需要的辅助空间增加
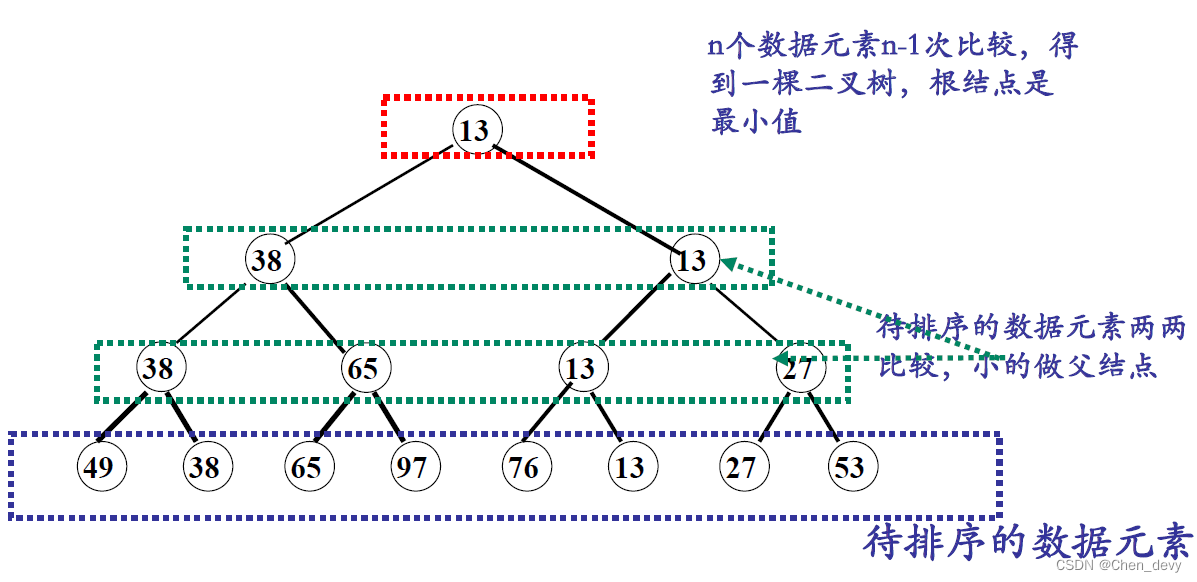
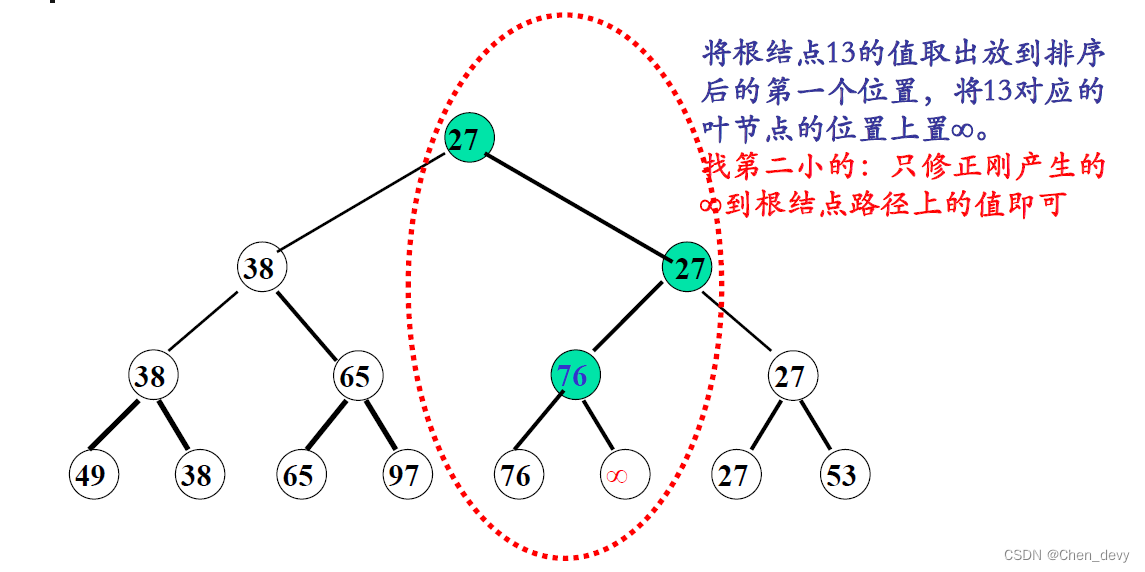
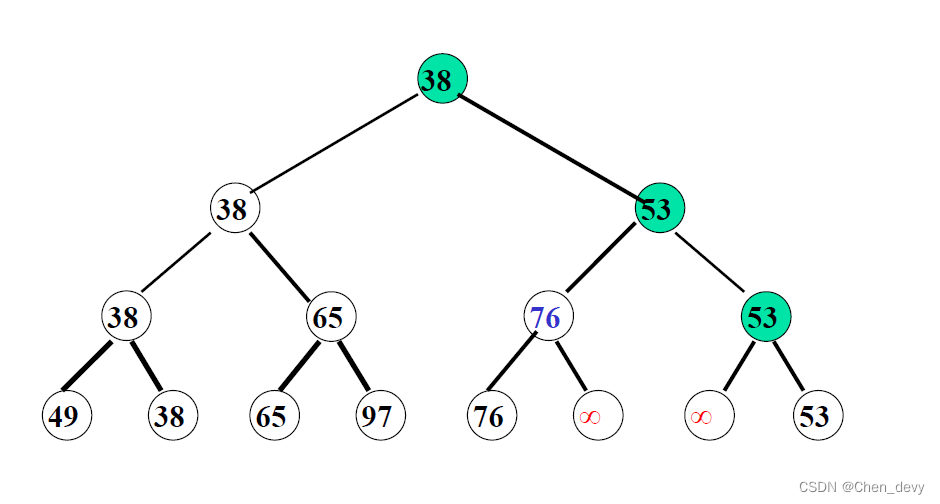
四、归并排序(2-路归并排序)
分治策略
算法评价:稳定!!!
时间复杂度为: O ( n l o g 2 n ) O(nlog_{2}n) O(nlog2n)
空间复杂度: O ( n ) O(n) O(n)

归并排序:每次将两个或两个以上的有序表组合成一个新的有序表
排序过程:
设初始序列含有n个记录,则可看成n个有序的子序列,每个子序列长度为1 两两合并,得到 n / 2 n/2 n/2 个长度为2或1的有序子序列
再两两合并,……如此重复,直至得到一个长度为n的有序序列为止
自底向上:
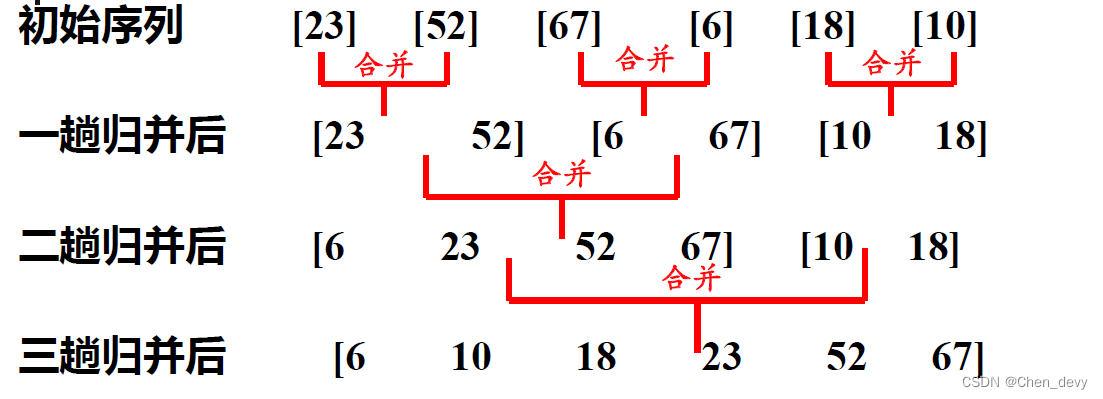
自项向下:

//自底向上
void Merge (ElemType SR[], Elemtype TR[], int i, int m, int n){ int j, k;// 将有序的序列 SR[s..m] 和 SR[m+1..t]归并为有序的序列 TR[s..t]for (j=m+1, k=i;i<=m && j<=n;++k){ // i为第一个有序序列 SR[s..m] 当前正在查看的数据,该序列的第一个数据元素在s处;// j为第二个有序序列 SR[m+1..t]当前正在查看的数据,该序列的第一个数据元素在m+1处;// k为合并后的有序序列 TR[s..t]的存放位置,第一个位置为sif (SR[i].key<=SR[j].key) TR[k] = SR[i++];else TR[k] = SR[j++];}if (i<=m)for(;i<=m;i++,k++) //第一个有序序列 还有数据没有比较,将其复制到合并后的序列;TR[k] = SR[i]; if (j<=n) for(;j<=n;j++,k++)// 第二个有序序列 还有数据没有比较,将其复制到合并后的序列 TR[k] = SR[j];
}
//自底向上 合并 合并 合并
void MSort ( ElemType SR[], ElemType TR1[], int s, int t )
{ // 将SR[s..t] 归并排序为 TR1[s..t]ElemType TR2[MAXSIZE]; int m;if (s==t) TR1[s]=SR[s];//序列中只有一个数据元素,序列自然有序else { //序列中包含2个或2个以上数据元素m = (s+t)/2;//计算序列的中间位置,以此为界划分为2个序列MSort (SR, TR2, s, m); //对第一个子序列递归调用归并排序算法,使其有序MSort (SR, TR2, m+1, t); //对第二个子序列递归调用归并排序算法,使其有序Merge (TR2, TR1, s, m, t); //将2个有序子序列合并为一个有序序列}
}2-路归并排序算法评价:
五、基数排序
不通过待排序数据元素之间的比较
根据关键字本身的性质进行排序
分配排序,桶排序,基数排序
1. 桶排序(适合元素关键字值集合并不大)

2. 基数排序
时间复杂度: O ( d ( n + 2 r d ) ) O(d(n+2rd)) O(d(n+2rd))
空间复杂度: O ( r d ) O(rd) O(rd)
方法一:优先级 由低到高

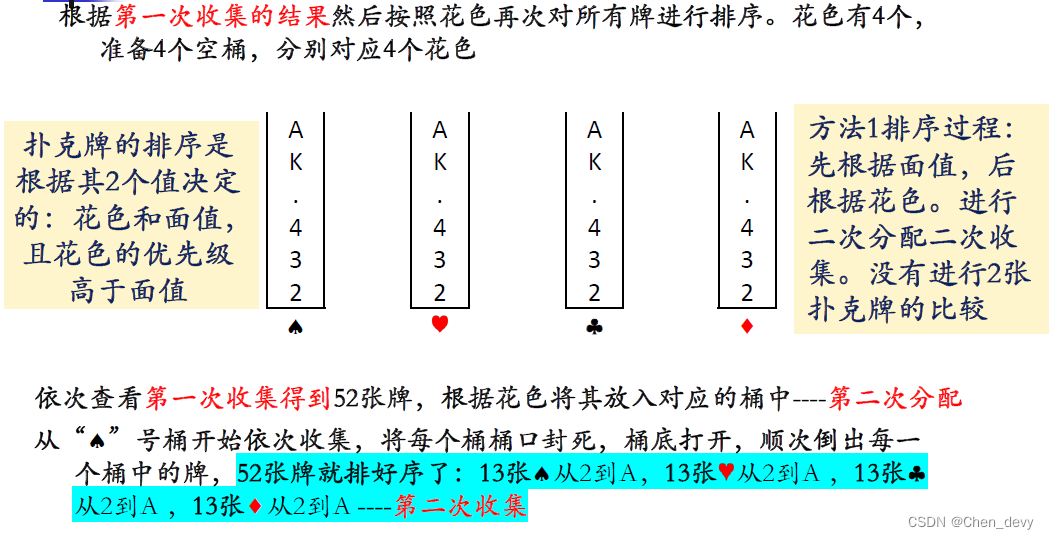
方法二 由高到低
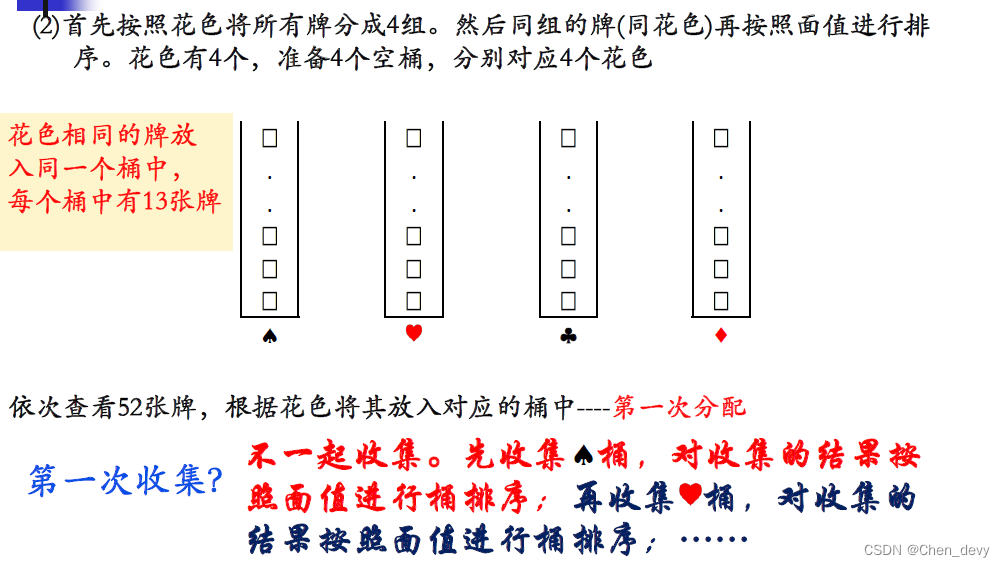
基数排序是一种借助“多关键字排序”的思想来实现“单关键字排序”的内部排序算法。
通常采用低位优先—简单方便





基数排序(Radix Sort)是一种非比较型排序算法,它通过将待排序的元素分成多个关键字进行排序,然后依次对每个关键字进行分配和收集,从而完成整个排序过程。基数排序适用于处理整数或字符串等类型的排序问题。下面是基数排序的详细分析和解释:
基数排序的基本原理
基数排序的基本思想是将待排序的记录(元素)看作是由多个关键字组成的,每次按一个关键字对记录进行分配和收集,逐步完成排序。通常有两种方法:
- 最高位优先法(MSD,Most Significant Digit):先按最高位进行排序,再按次高位进行排序,依此类推,直到按最低位排序。
- 最低位优先法(LSD,Least Significant Digit):先按最低位进行排序,再按次低位进行排序,依此类推,直到按最高位排序。
基数排序的实现步骤
基数排序可以分为以下几个步骤进行:
-
初始化静态链表:
- 将待排序的数据元素存放在一个静态链表中,初始链表的顺序与原始数据的顺序相同。
- 用
next指针将所有数据元素连接起来,最后一个元素的next指针为-1,表示链表的尾结点。
-
分配(Distribute):
- 按照当前关键字(从最低位开始)对数据元素进行分配。
- 根据当前关键字的值,将数据元素分配到不同的桶(或链表)中。
-
收集(Collect):
- 将所有桶中的数据元素按顺序收集起来,重新连接成一个链表。
- 完成一次对当前关键字的排序。
-
重复上述步骤:
- 对下一个关键字重复进行分配和收集,直到所有关键字都排序完毕。
基数排序的代码实现
以下是给出的基数排序的代码实现及其详细分析:
#define MAX_NUM_OF_KEY 8//关键字个数最大值
#define radix10//队列个数
#define MAX_SPACE 1000
typedef struct {Keystype keys[MAX_NUM_OF_KEY];//……int next;
}SLCell;typedef struct {SLCell R[MAX_SPACE];int keynum; // 关键字个数int recnum; // 待排序数据元素个数
} SLList;// 定义一个数组类型,用于存放每个桶的头指针和尾指针
typedef int ArrType[radix];void Distribute(SLCell R[], int i, ArrType &f, ArrType &r, int head) {// 初始化每个桶的头指针数组 f,全部设置为 -1,表示空桶for (int j = 0; j < radix; j++) f[j] = -1;// 遍历链表,将每个元素按第 i 个关键字值分配到对应的桶中for (int p = head; p != -1; p = R[p].next) { int j = ord(R[p].keys[i]); // 取 R[p] 的第 i 个关键字// 如果当前桶是空的,则设置该桶的头指针为当前元素if (f[j] == -1)f[j] = p;else R[r[j]].next = p; // 否则将当前元素链接到当前桶的尾部r[j] = p; // 更新当前桶的尾指针为当前元素}
}void Collect(SLCell R[], int i, ArrType f, ArrType r, int &head) {// 找到第一个非空的桶,并设置为链表的头int j = 0;while (j < radix && f[j] == -1)j++;head = f[j];// 设置 t 为当前连接链表的尾部int t = r[j];// 依次连接其他桶,形成新的链表while (j < radix) {j++;while (j < radix && f[j] == -1)j++;if (j < radix) {R[t].next = f[j]; // 将 t 的 next 指向 f[j]t = r[j]; // 更新 t 为当前桶的尾部}}// 最后一个节点的 next 设为 -1,表示链表结束R[t].next = -1;
}void RadixSort(SLList &L) {// 初始化静态链表,将数据元素按初始顺序连接起来for (int j = 0; j < L.recnum - 1; j++) L.R[j].next = j + 1; // 设置每个元素的 next 指向下一个元素L.R[L.recnum - 1].next = -1; // 最后一个元素的 next 指向 -1,表示链表结束int head = 0; // 初始化链表的头指针为第一个元素ArrType f, r; // 桶的头指针数组 f 和尾指针数组 r// 对每个关键字依次进行分配和收集for (int i = 0; i < L.keynum; i++) {Distribute(L.R, i, f, r, head); // 根据第 i 个关键字进行分配Collect(L.R, i, f, r, head); // 将分配好的桶按顺序收集成新的链表}
}下面是逐行解释给出的基数排序代码:
typedef struct {SLCell R[MAX_SPACE];int keynum; // 关键字个数int recnum; // 待排序数据元素个数
} SLList;// 定义一个数组类型,用于存放每个桶的头指针和尾指针
typedef int ArrType[radix];void Distribute(SLCell R[], int i, ArrType &f, ArrType &r, int head) {// 初始化每个桶的头指针数组 f,全部设置为 -1,表示空桶for (int j = 0; j < radix; j++) f[j] = -1;// 遍历链表,将每个元素按第 i 个关键字值分配到对应的桶中for (int p = head; p != -1; p = R[p].next) { int j = ord(R[p].keys[i]); // 取 R[p] 的第 i 个关键字// 如果当前桶是空的,则设置该桶的头指针为当前元素if (f[j] == -1)f[j] = p;else R[r[j]].next = p; // 否则将当前元素链接到当前桶的尾部r[j] = p; // 更新当前桶的尾指针为当前元素}
}void Collect(SLCell R[], int i, ArrType f, ArrType r, int &head) {// 找到第一个非空的桶,并设置为链表的头int j = 0;while (j < radix && f[j] == -1)j++;head = f[j];// 设置 t 为当前连接链表的尾部int t = r[j];// 依次连接其他桶,形成新的链表while (j < radix) {j++;while (j < radix && f[j] == -1)j++;if (j < radix) {R[t].next = f[j]; // 将 t 的 next 指向 f[j]t = r[j]; // 更新 t 为当前桶的尾部}}// 最后一个节点的 next 设为 -1,表示链表结束R[t].next = -1;
}void RadixSort(SLList &L) {// 初始化静态链表,将数据元素按初始顺序连接起来for (int j = 0; j < L.recnum - 1; j++) L.R[j].next = j + 1; // 设置每个元素的 next 指向下一个元素L.R[L.recnum - 1].next = -1; // 最后一个元素的 next 指向 -1,表示链表结束int head = 0; // 初始化链表的头指针为第一个元素ArrType f, r; // 桶的头指针数组 f 和尾指针数组 r// 对每个关键字依次进行分配和收集for (int i = 0; i < L.keynum; i++) {Distribute(L.R, i, f, r, head); // 根据第 i 个关键字进行分配Collect(L.R, i, f, r, head); // 将分配好的桶按顺序收集成新的链表}
}
- 数据结构定义:
typedef struct {SLCell R[MAX_SPACE]; // 存放待排序数据元素的数组int keynum; // 关键字个数int recnum; // 待排序数据元素个数
} SLList;
SLCell R[MAX_SPACE]:存放待排序数据元素的数组。int keynum:关键字的个数。int recnum:待排序数据元素的个数。
typedef int ArrType[radix];
- 定义一个数组类型,用于存放每个桶的头指针和尾指针。
- 分配函数
Distribute:
void Distribute(SLCell R[], int i, ArrType &f, ArrType &r, int head) {// 初始化每个桶的头指针数组 f,全部设置为 -1,表示空桶for (int j = 0; j < radix; j++) f[j] = -1;// 遍历链表,将每个元素按第 i 个关键字值分配到对应的桶中for (int p = head; p != -1; p = R[p].next) { int j = ord(R[p].keys[i]); // 示意性操,取 R[p] 的第 i 个关键字// 如果当前桶是空的,则设置该桶的头指针为当前元素if (f[j] == -1)f[j] = p;else R[r[j]].next = p; // 否则将当前元素链接到当前桶的尾部r[j] = p; // 更新当前桶的尾指针为当前元素}
}
Distribute函数按第i个关键字值对数据元素进行分配。- 初始化桶的头指针数组
f为-1,表示空桶。 - 遍历链表,将每个数据元素按当前关键字值分配到对应的桶中。
- 更新桶的头指针和尾指针。
- 收集函数
Collect:
void Collect(SLCell R[], int i, ArrType f, ArrType r, int &head) {// 找到第一个非空的桶,并设置为链表的头int j = 0;while (j < radix && f[j] == -1)j++;//找到第一个 不是-1的head = f[j];// 设置 t 为当前连接链表的尾部int t = r[j];// 依次连接其他桶,形成新的链表while (j < radix) {// j++;while (j < radix && f[j] == -1)j++;//找到下一个 不是-1的if (f[j]!=-1) {R[t].next = f[j]; // 将 t 的 next 指向 f[j]t = r[j]; // 更新 t 为当前桶的尾部}}// 最后一个节点的 next 设为 -1,表示链表结束R[t].next = -1;
}
Collect函数将分配好的桶按顺序收集成新的链表。- 找到第一个非空的桶,设置为链表的头。
- 依次连接其他桶,形成新的链表。
- 设置最后一个节点的
next为-1,表示链表结束。
- 基数排序主函数
RadixSort:
void RadixSort(SLList &L) {// 初始化静态链表,将数据元素按初始顺序连接起来for (int j = 0; j < L.recnum - 1; j++) L.R[j].next = j + 1; // 设置每个元素的 next 指向下一个元素L.R[L.recnum - 1].next = -1; // 最后一个元素的 next 指向 -1,表示链表结束int head = 0; // 初始化链表的头指针为第一个元素ArrType f, r; // 桶的头指针数组 f 和尾指针数组 r// 对每个关键字依次进行分配和收集for (int i = 0; i < L.keynum; i++) {Distribute(L.R, i, f, r, head); // 根据第 i 个关键字进行分配Collect(L.R, i, f, r, head); // 将分配好的桶按顺序收集成新的链表}
}
RadixSort函数是基数排序的主函数。- 初始化静态链表,将数据元素按初始顺序连接起来。
- 初始化链表的头指针为第一个元素。
- 定义桶的头指针数组
f和尾指针数组r。 - 对每个关键字依次进行分配和收集,完成排序。
时间性能
平均的时间性能
时间复杂度为O(nlogn):快速排序、堆排序和归并排序
时间复杂度为 O ( n 2 ) O(n^2) O(n2):直接插入、冒泡和简单选择排序
时间复杂度为 O ( n ) O(n) O(n): 基数排序
当待排记录序列按关键字顺序有序时
直接插入和冒泡排序: O ( n ) O(n) O(n)
快速排序: O ( n 2 ) O(n_2) O(n2) 。
简单选择排序、堆排序和归并排序的时间性能不随记录序列中关键字的分布而改变。
空间性能指的是排序过程中所需的辅助空间大小
所有的简单排序方法(包括:直接插入、起泡和简单选择) 和堆排序的空间复杂度为O(1);
快速排序为O(logn),为递归程序执行过程中,栈所需的辅助空间;
归并排序所需辅助空间最多,其空间复杂度为 O(n);
链式基数排序需附设队列首尾指针,则空间复杂度为 O(rd)。
这篇关于【数据结构】排序(直接插入、折半插入、希尔排序、快排、冒泡、选择、堆排序、归并排序、基数排序)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!