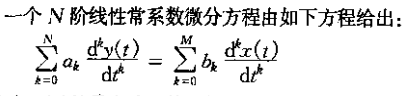本文主要是介绍关于N阶常系数差分方程和微分方程的对比易误点(d ' y(t)/dt 对应 y[n - 1] ? ),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Linear Constant-coefficient difference equations
这里有个容易“让人困惑”的地方,仔细观察两个方程,加上这里书上说了一句“1.109式(图中上面的公式),对应的离散时间方程是下面的方程”
发现会有一种感觉,"既然是对应的,那么这里d ' y(t)/dt 岂不是对应 y[n - 1] (当k = 1时)"
正是这样,我就陷入了深深的困惑。。。
会觉得“怎么连续领域内的一阶导数等于离散领域内的偏移即可?”想不明白
实质上这样思考是不对的。
陷入了误区, 这两个方程针对的对象不同,前者是为了刻画连续领域而建立的模型,后者是离散领域的。
这个方程之所以成立,就是因为它刻画的是输入和输出之间的关系,对于LIT系统,总能找到相应的系数,使得输入信号的各个阶次的导数的线性组合能够等于输出信号的各阶导数的线性组合。
input --> | system | -->output
而对于离散系统来说,LTI系统的输出仅可能和输入或者输出(有反馈的情况),有关系,
而为了描述建立这种关系,于是就会有下面的公式
当系统有反馈的时候k就不等于1了,右边作为系统的单独输入量的各种组合.
举个例子
y[n] = y[n-1] + x[n];
这个系统描述的就是当前系统的输出量y[n] 取决于前一时刻系统的输出量加上当前系统的输入量(这家伙是个正反馈).
x[n] ---(+)-->| system | ---> y[n]
^--------------------|
把系统描述方程稍作变形,把y[] 相关项和x[]相关项分别分离在等式的左右两边,于是有
y[n] - y[n-1] =x[n];
因此,他们仅仅是对不同系统构建的描述方法而已,都是尝试利用已知的系统输入输出建立描述系统的模型.
连续系统里面,系统的阶数会对输入输出有影响,于是会用到微分,
离散系统里面,系统的输入输出的偏移量有可能会影响系统的输出,于是会用到系统的偏移量。
不要陷入“d ' y(t)/dt 对应 y[n - 1] ”对比性的困惑
这篇关于关于N阶常系数差分方程和微分方程的对比易误点(d ' y(t)/dt 对应 y[n - 1] ? )的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!