本文主要是介绍DFS --- Depth First Search 深度优先搜索算法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Depth First Search
原理还是去看《DSAA》,这里着重分析实现策略。
如果对于图这种数据结构不熟悉,这个BFS一般是搞不定的...
下面分别是无向图的邻接表实现和邻接矩阵实现
http://blog.csdn.net/cinmyheart/article/details/41381845
http://blog.csdn.net/cinmyheart/article/details/41370465
-----------------------------------------------------------
/************************************************************
code file : dfs.h
code writer : EOF
code date : 2014.11.22
e-mail : jasonleaster@gmail.comcode description:This file is a header file for out test program.
We abstract the data structure -- Graph here. And we also
declare some useful API to construct out naive graph :)************************************************************/#ifndef _DFS_H_
#define _DFS_H_#include <stdio.h>#include <stdlib.h>#define CONNECTED 1#define DISCONNECTED 0#define SUCCESS 0#define FAILED -1#define UN_VISITED 0#define VISITED 1#define ENTRY_POINT 3struct visited{int array[0];};struct vertex{int value;struct vertex* next;struct vertex* end;};struct graph{int num_vertex;int num_edge;struct vertex adjacent[0];};void dfs(struct graph* p_graph,struct vertex* p_vertex,struct visited* p_visited);struct graph* init_graph(int vertex,int edge);void release_graph(struct graph* p_graph);int add_edge(struct graph* p_graph,char from_v,char to_v);int print_graph(struct graph* p_graph);#endif关键的,对于DFS的实现
这个函数我设计接受三个参数(指针),p_graph指向图,p_vertex指向节点,p_visited指向标记“数组”(动态分配得的结构体)
/*********************************************************
code writer : EOF
code date : 2014.11.24
code file : dfs.c
e-mail : jasonleaster@gmail.comCode description:This function @dfs() is a implementation of
"Depth first search" which is based on recursion.**********************************************************/#include "dfs.h"void dfs(struct graph* p_graph,struct vertex* p_vertex,struct visited* p_visited)
{if(!p_vertex){return;}p_visited->array[p_vertex->value] = VISITED;printf("%d->",p_vertex->value);for(p_vertex = p_vertex->next;!!p_vertex;p_vertex = p_vertex->next){if(p_visited->array[p_vertex->value] == UN_VISITED){dfs(p_graph,&(p_graph->adjacent[p_vertex->value]),p_visited);}}printf("\n");
}既然是深度优先搜索,而且对于已经检索到的数据会有“全局标记”(这里采用的是同一动态内存分配所得内存区域)。
那么我们使可以利用圈图进行测试的
比方说
节点链接是个圈: 1->2->3->4->1,这种,首尾相连的圈。
从任何节点进入,都可以停下并且检索完所有的节点。
我们的测试程序:
/****************************************************************
code file : test_graph.c
code writer : EOF
code date : 2014.11.22
e-mail : jasonleaster@gmail.comcode description:Here , we use this program to call some API which would
construct a ADT--graph and test it.*****************************************************************/
#include "dfs.h"int main()
{struct graph* p_graph = NULL;FILE* fp = fopen("./text.txt","r+");if(!fp){printf("fopen() failed!\n");return 0;}int ret = 0;int vertex = 0;int edge = 0;int from_v = 0;int to_v = 0;fscanf(fp,"%d",&vertex);fscanf(fp,"%d",&edge);p_graph = init_graph(vertex,edge);int temp = 0;for(temp = 0;temp < edge;temp++){/*** I think it's necessary to check the returned value** of scanf() family.*/ret = fscanf(fp,"%d %d",&from_v,&to_v);if(ret != 2){break;}add_edge(p_graph,from_v,to_v);}struct visited* p_visited = (struct visited*)malloc(sizeof(struct visited) +\sizeof(int)*(p_graph->num_vertex));for(temp = 0;temp < p_graph->num_vertex;temp++){p_visited->array[temp] = UN_VISITED;} print_graph(p_graph);/*** Here, we start to DFS.*/dfs(p_graph,&(p_graph->adjacent[ENTRY_POINT]),p_visited);release_graph(p_graph);free(p_visited);p_visited = NULL;fclose(fp);return 0;
}测试文本数据text.txt:
5
5
1 2
2 3
3 4
4 1测试结果:
同样的,我们可以用其他的图进行测试:
测试文本:
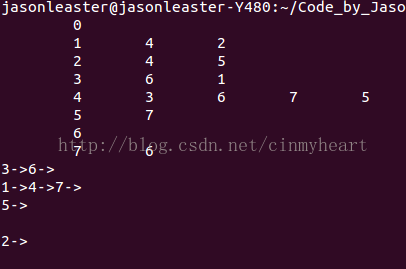
8个节点,12条边的图
8
12
3 6
3 1
1 4
1 2
4 3
4 6
4 7
4 5
7 6
2 4
2 5
5 7测试结果:
这篇关于DFS --- Depth First Search 深度优先搜索算法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!