本文主要是介绍一维时间序列突变检测方法(小波等,MATLAB R2021B),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
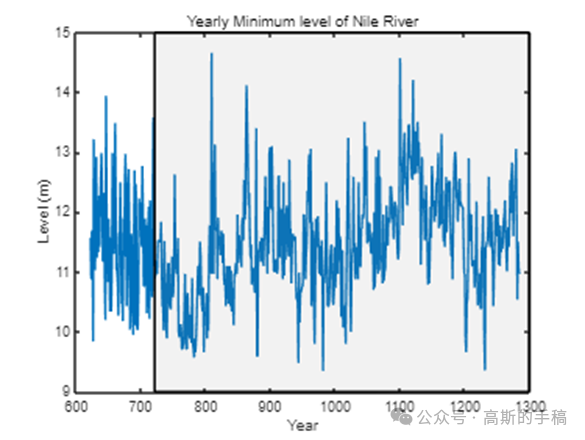
信号的突变点检测问题是指在生产实践中,反映各种系统工作状态的信号,可能因为受到不同类型的噪声或外界干扰而发生了信号突变,导致严重失真的信号出现,因此必须探测突变出现的起点和终点。研究目的在于设计出检测方案,可以最快地检测出系统中信号非正常变化的时刻,作出后续处理,以减小损失。目前在国内,信号的突变点检测课题在滚动轴承、水利水电、智能空间行为识别等许多工程实践和科学研究领域已得到广泛研究。
自上世纪经典DSP方法提出并被逐渐成熟地应用以来,信号的突变点检测问题一直是一个较热的研究课题。对于信号突变点检测问题,目前已经提出了许多有效的经典DSP方法,例如经典的基于信号能量的检测法,然而其易于受噪声干扰且需要延迟一段时间以计算能量,因此发展了不少改进方法,比如基于累积和CUSUM的方式因具有良好的性能而得到广泛应用。CUSUM具有递归形式能够进行实时更新操作,计算效率比较高。虽然最初提出CUSUM来处理单个数据流,但是目前基于CUSUM的检测算法大多利用了来自多个传感器的信息。CUSUM通常需要信号突变前和突变后的统计信息作为检测的前提,在某些情形下,信号发生突变后的分布模型的统计信息是可以获得的,但在更一般场景中,由于突变原因多样且往往未知,变更后的模型发生了根本改变,突变后的统计信息是无法获得或预知的。又有科研人员提出了突变信息快速检测方法,快速检测方法旨在仅仅利用少量突变后的数据来进行训练,以得到信号突变后的模型,以此来最大程度地减少检测延迟。放眼许多应用场景,信号突变以后的分布模型可能来自一组潜在的可能模型,换句话说,变更后模型有多种假设。例如,检测风机轴承故障时,引起该故障的原因故障可能是外圈故障或内圈故障、滚子缺陷或和保存架故障等。在快速检测方法中,贝叶斯方法的效果比较好,本质上该方法就是提出了信号突变后的几种备选模型,然后通过算法来估计出最优的突变后的信号分布情况,进行进一步处理,从一定意义上放宽了很多场景中对突变后信号信息的依赖,但依然是治标不治本。
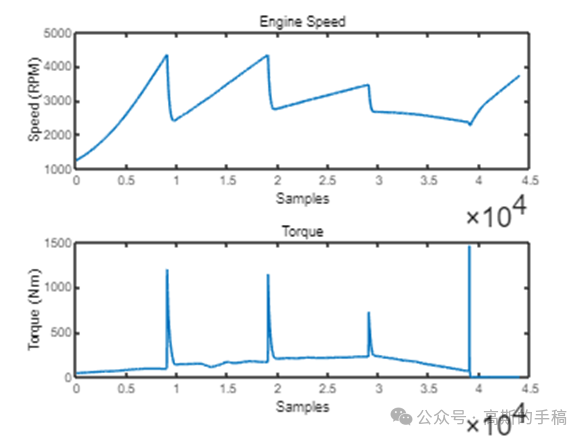
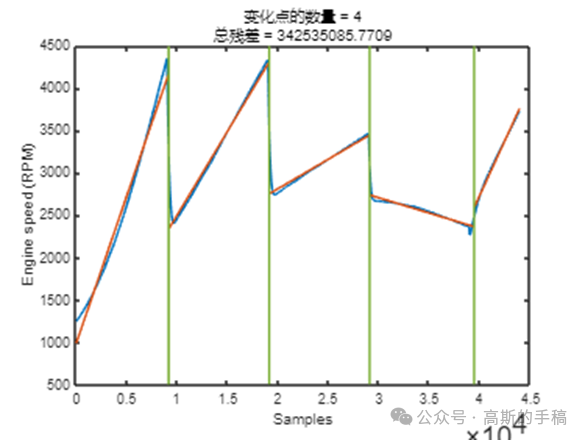
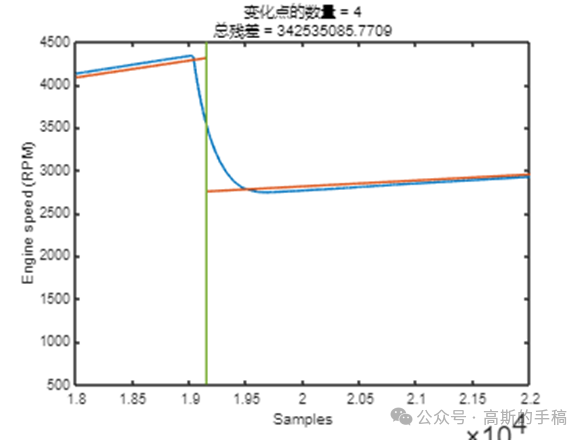
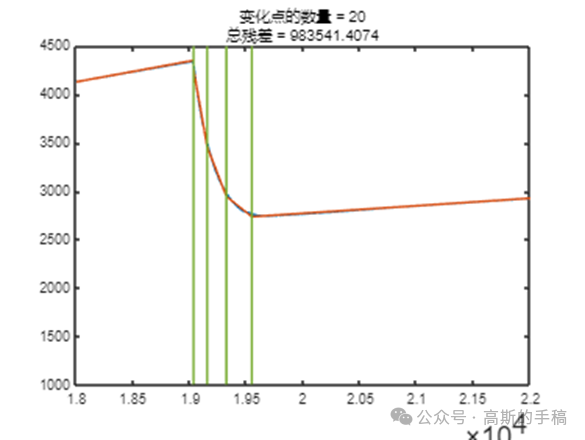
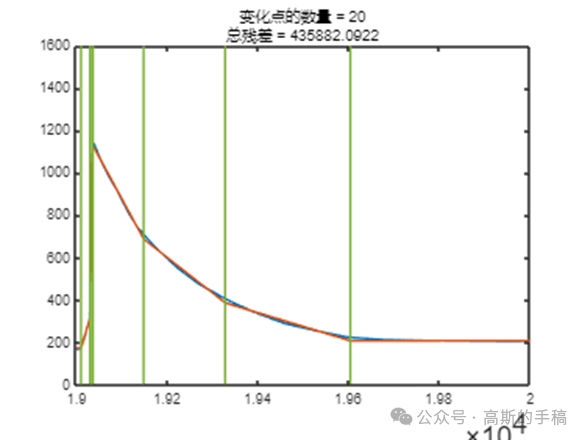
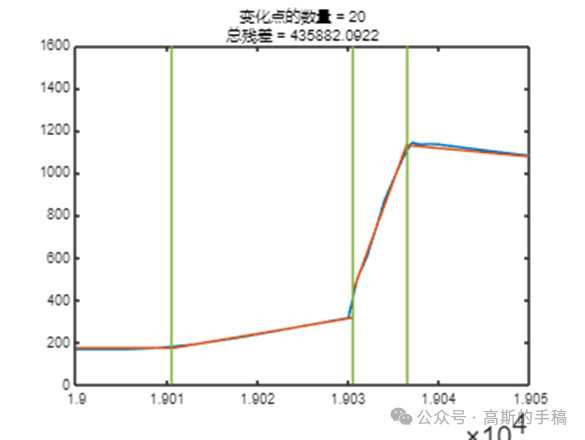
鉴于此,采用小波分析等方法对一维时间序列进行突变检测,运行环境为MATLAB R2021B。
function residue = cpnochange(x, statistic)
% compute total residual error in the absence of changes
n = size(x,2);
if n==0residue = NaN;
elseif strcmp(statistic,'mean')residue = n*sum(var(x,1,2));
elseif strcmp(statistic,'rms')residue = sum(n*log(sum(x.^2,2)/n));
elseif strcmp(statistic,'std')residue = sum(n*log(var(x,1,2)));
elseif strcmp(statistic,'linear')residue = sum(n*var(x,1,2) - sum((x-mean(x,2)).*((1:n)-mean(1:n)),2).^2 / (n*var(1:n,1)));
完整代码可通过知乎学术咨询获得:https://www.zhihu.com/consult/people/792359672131756032?isMe=1
end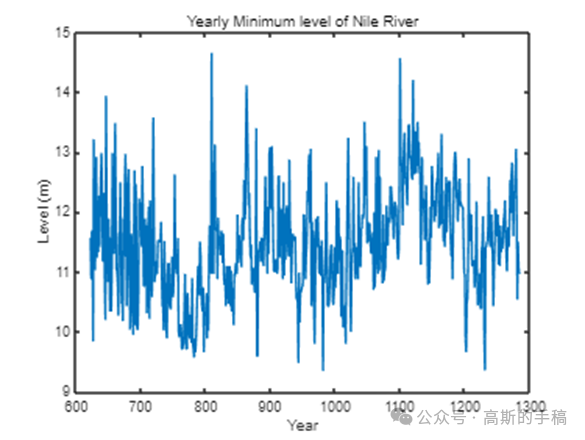
工学博士,担任《Mechanical System and Signal Processing》《中国电机工程学报》《控制与决策》等期刊审稿专家,擅长领域:现代信号处理,机器学习,深度学习,数字孪生,时间序列分析,设备缺陷检测、设备异常检测、设备智能故障诊断与健康管理PHM等。
这篇关于一维时间序列突变检测方法(小波等,MATLAB R2021B)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






