Neural Networks and Deep Learning(一)

本文主要是介绍Neural Networks and Deep Learning(一)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Neural Networks and Deep Learning学习（一）

之间学习CNN核卷积，ufldl教程看了大部分，现在系统的过一遍深度学习，加强自己对深度学习和神经网络的理解。

这只是学习笔记，不是教程，只是本人学习此文档的理解和一些见解

第一章理解

1） 权重之间的连线可以看成一种“因素”，其权重则可以表示该“因素”的可能性。如下图所示，b由一系类的a决定的，a与b之间的连线表示a选择b发生的概率，b的偏置则表示自身的权值

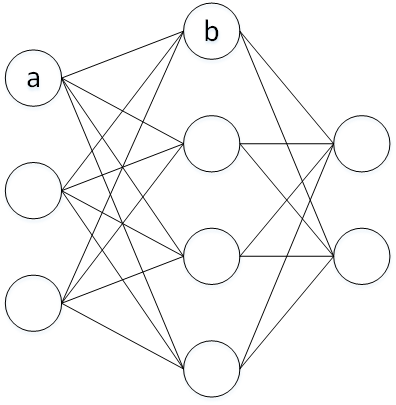
把权重的总和与阈值比较得到输出，

$$output= \begin{cases} 0 & if & \sum_{j}w_jx_j\le threshold\\ 1 & if & \sum_{j}w_jx_j > threshold \end{cases}$$
然后把阈值写在左边作为偏置
$$output= \begin{cases} 0 & if & w_j\cdot x_j\le 0\\ 1 & if & w_j\cdot x_j > 0 \end{cases}$$
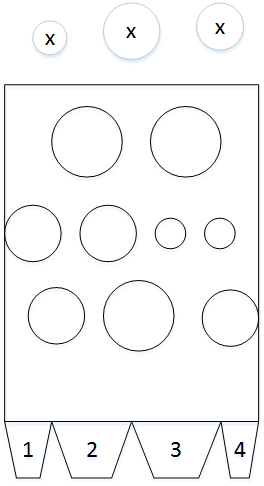
还可以理解如下图所示：

图中最上面小球为输入数据，小球不同的大小表示不同的输入数据；中间的矩形则表示神经网络，其内部不同大小的小球和不同位置的小球表示不同的参数，其中位置可以看成权重，大小可以看成偏置；底部的梯形表示输出的结果，不同的标号表示不同的输出结果。神经网络的训练就是调节矩形内部的小球，使对于不同的输出小球，最终会落在合理的输出矩形中。

2） 神经网络就是利用权重（偏置）的微小改变引起输入的微小变化。

练习1_2_1 把一个感知神经网络的权值和偏置乘以一个正常数c，证明网络的行为没有改变。
证明： 感知机的输出结果是0，1。当输出结果大于1时，output为1；当输出小于0时，output为0。则当乘以c时$c\cdot wx + c\cdot b = c\cdot (wx + b)$，其output受到$wx +ｂ$的影响。

练习1_2_2 S型神经元（激活函数由sigmoid构成），假设$w\cdot x+b\ne 0$，把权重和偏置乘以一个正常数c，证明当$c\to \infty$ 时，S型神经元网络和感知器网络完全一致。若$w\cdot x+b=0$，结果如何？
证明： 由于$w\cdot x+b\ne 0$，则$c\cdot (wx+b)\ne 0(c>0)$，当$w\cdot x+b> 0$时，由$c\to \infty$ 得到$c\cdot (wx+b)\to +\infty$，则$\sigma(c\cdot (ws + b))\approx1$；当$w\cdot x+b<0$时，由$c\to \infty$ 得到$c\cdot (wx+b)\to -\infty$，则$\sigma(c\cdot (ws + b))\approx 0$。若$w\cdot x+b= 0$，$c\cdot (wx +ｂ)＝０$，无变化。

练习1_4 在输出层后增加一层使用2进制层表示输出，设置其权重。
答：： 假设增加4个神经元，输出0000表示0，输出0001表示1 ，…。只需要设置10个输出与相应位相连的权重为1即可。

3） 为什么使用二次代价（损失函数），而不是直接最大化，使目标最优？
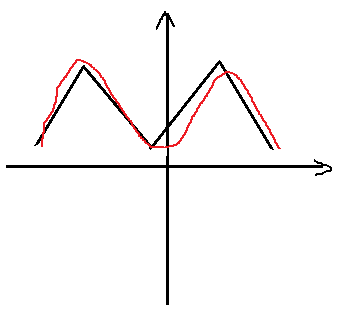
答： 由于权重和偏置组成的函数不是一个平滑函数，对权重的微小改变不会影响结果，使用二次代价函数可用微小的改变取得较好的效果。如下图所示：

黑色的为正确的曲线，红的为拟合的曲线，如果直接调节红色曲线来实现拟合比较困难，不容易调节具体的参数，如果使用与原始曲线的“差距”来进行调节，就可以有针对的进行调节。

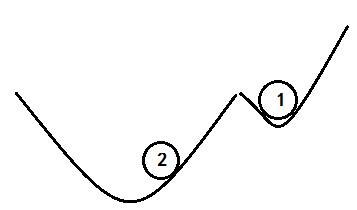
4） 梯度下降法：把函数想象成一个山谷，求最小值就是小球从山谷的斜坡落下来到达山底，由于受到“摩擦”，“重力”不同，小球的下降的方式不同。梯度可以看成下降的方向，学习率则为下降速度，其值不能太大或者太小，太大无法到达最低点，太小容易陷入局部最优且速度太慢，如下图所示，小球1速度太小，小球2速度太大。$\Delta C \approx \nabla C \cdot \Delta v$ 说明$\nabla C$把v的变化关联为C的变化。

练习1_5_1 证明：$\nabla C \cdot \Delta v$取得最小值的$\Delta v$为$\nabla C \cdot \Delta v = -\eta \nabla C$。
证明：由柯西-施瓦茨不等式$|<x,y>|\le||x||\cdot ||y||$得到：

$$\begin{align*} &||\Delta v||\cdot ||\nabla C|| \ge \nabla C\cdot \Delta v\\ \Rightarrow &\nabla C\cdot \Delta v \ge -||\Delta v||\cdot ||\nabla C||\\ &=-\frac{||\Delta v||\cdot ||\nabla C||}{||\nabla C||^{2}}\cdot \nabla C \cdot \nabla C\\ &=-\frac{||\Delta v||}{||\nabla C||}\cdot \nabla C \cdot \nabla C\\ &=-\eta \nabla C \cdot \nabla C\\ \Rightarrow &\Delta v \ge -\eta \nabla C \end{align*}$$

练习1_5_2 梯度下降法在一元函数的解释。
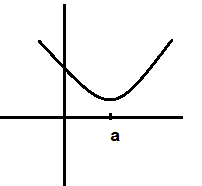
答： 一元函数图像如下：

在a的左边时，梯度为曲线的斜率，其值为负值，随着x的增大，即$\Delta x>0$，$\Delta y \approx \nabla C \cdot \Delta x$，$\Delta y<0$，y降低。当在a的右边时，梯度为正值，随着x的减小，即$\Delta x<0$，$\Delta y \approx \nabla C \cdot \Delta x$，$\Delta y<0$，y降低。则使用梯度下降法，总会到达最低点。

5） 当直接求输入数据的偏导数时，代价非常的大，百万的输入数据，其二阶偏导数则需要数万亿（百万的平方的一半$\frac{\partial^2C}{\partial v_i \partial v_k}=\frac{\partial^2C}{\partial v_k \partial v_i}$）,这就引出使用权重和偏置，对权重和偏置求导，推导出更新函数。

练习1_5_3 在线学习优点（on-line learing，把批量数据大小设为1，每次输入一个数据，就更新权重）。
答：这个名词提出较早的时间，很难找到关于其理论的东西，网上的在线学习都是教育方面的，最后在一本英文书On-Line Learning in Neural Netwoks找到了相关的知识。

优点：
连续的on-line learning中，梯度下降法是在许多强大和常用的方法中的微分误差法，对于非平稳情况特别有效。
缺点：
a>训练的灵明度。减慢了训练，影响收敛到固定点的能力。
b>许多好的优化方法依赖于一个固定的误差面，而on-line learning产生随机误差面。
c>Bayesian提供了一个成功的batch learning，而on-line learning不会储存过去的信息，受到限制。

练习1_6 神经网络传播方程。
答：

$$\begin{align*} a &= \sigma(w_1x+b_1)\\ a^{'}&=\sigma(w_2x+b_2)\\ &=\sigma(w_2\cdot \sigma(w_1x +b_1)＋ｂ_2)\\ &=\frac{1}{1+e^{-w_2a-b_2}} \end{align*}$$

代码说明

分别建立了3个文件，Network.py, mnist_loader.py, train.py，作为建立网络， 加载数据和测试计算。具体代码如下：
Network.py

# coding="utf-8"
import numpy as npclass Network(object):# 网络初始化函数，初始化每层的权重和偏置def __init__(self, sizes):self.num_layers = len(sizes)self.sizes = sizesself.biases = [np.random.randn(y, 1) for y in sizes[1:]]self.weights = [np.random.randn(y, x) for x, y in zip(sizes[:-1], sizes[1:])]# 前向传播 激活函数使用sigmoiddef feedforward(self, a):for b, w in zip(self.biases, self.weights):a = sigmoid(np.dot(w, a) + b)return a# 随机梯度下降法用于计算参数def SGD(self, training_data, epochs, mini_batch_size, eta, test_data=None):# 判断是否在每一层进行测试结果计算if test_data:n_test = len(test_data)n = len(training_data)# 进行epochs次计算for j in xrange(epochs):# 将序列的所有元素从新排列np.random.shuffle(training_data)# 创建batchesDatamini_batches = [training_data[k:k + mini_batch_size] for k in xrange(0, n, mini_batch_size)]for mini_batch in mini_batches:# 更新参数self.update_mini_batch(mini_batch, eta)if test_data:print "Epoch {0}: {1} / {2}".format(j, self.evaluate(test_data), n_test)else:print "Epoch {0} complete".format(j)# 参数的更新def update_mini_batch(self, mini_batch, eta):# 初始化梯度nabla_b = [np.zeros(b.shape) for b in self.biases]nabla_w = [np.zeros(w.shape) for w in self.weights]for x,y in mini_batch:# 梯度的计算delta_nabla_b, delta_nabla_w = self.backprop(x, y)nabla_b = [nb + dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]nabla_w = [nw + dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]self.weights = [w - (eta/len(mini_batch))*nw for w, nw in zip(self.biases, nabla_w)]self.biases = [b - (eta/len(mini_batch))*nb for b, nb in zip(self.biases, nabla_b)]# 反向传播计算梯度def backprop(self, x, y):nabla_b = [np.zeros(b.shape) for b in self.biases]nabla_w = [np.zeros(w.shape) for w in self.weights]# 激活层值activation = xactivations = [x]zs = []for b, w in zip(self.biases, self.weights):z = np.dot(w, activation) + bzs.append(z)activation = sigmoid(z)activations.append(activation)# 求出残差 具体导见ufldl教程delta = self.cost_derivative(activations[-1], y) * sigmoid_prime(zs[-1])nabla_b[-1] = deltanabla_w[-1] = np.dot(delta, activations[-2].transpose())# l-1 ... 1 层的梯度计算for l in xrange(2, self.num_layers):z = zs[-l]sp = sigmoid_prime(z)delta = np.dot(self.weights[-l + 1].transpose(), delta) * spnabla_b[-l] = deltanabla_w[-l] = np.dot(delta, activations[-l - 1].transpose())return (nabla_b, nabla_w)# 测试值def evaluate(self, test_data):test_results = [(np.argmax(self.feedforward(x)), y) for (x, y) in test_data]return sum(int(x == y) for (x, y) in test_results)# 最后一层残差计算def cost_derivative(self, output_activations, y):return (output_activations - y)# 激活函数
def sigmoid(z):return 1.0 / (1.0 + np.exp(-z))#激活函数导数
def sigmoid_prime(z):return sigmoid(z)*(1 - sigmoid(z))

mnist_loader.py

# coding="utf-8"
import cPickle
import gzipimport numpy as np# 加载数据
def load_data():f = gzip.open('./data/mnist.pkl.gz', 'rb')training_data, validation_data, test_data = cPickle.load(f)f.close()return (training_data, validation_data, test_data)def load_data_wrapper():tr_d, va_d, te_d = load_data()training_inputs = [np.reshape(x, (784, 1)) for x in tr_d[0]]training_results = [vectorized_result(y) for y in tr_d[1]]training_data = zip(training_inputs, training_results)validation_inputs = [np.reshape(x, (784, 1)) for x in va_d[0]]validation_data = zip(validation_inputs, va_d[1])test_inputs = [np.reshape(x, (784, 1)) for x in te_d[0]]test_data = zip(test_inputs, te_d[1])return (training_data, validation_data, test_data)def vectorized_result(j):e = np.zeros((10, 1))e[j] = 1.0return e

train.py

# coding="utf-8"
import mnist_loader
import Network
# 测试程序# 加载数据
training_data, validation_data, test_data = mnist_loader.load_data_wrapper()
# 建立网络
net = Network.Network([784, 100, 10])
# 随机梯度下降法计算网络
net.SGD(training_data, 30, 10, 3.0, test_data)

这篇关于Neural Networks and Deep Learning(一)的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---