本文主要是介绍【Self-Attention——Transform—Bert】相关的基础理论,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1.Self-Attention模型图解

传统的循环神经网络,如上左图1,并不能解决并行化的问题,右图就是一个self-Attention可以实现并行化,并且能解决对于所有信息的读取利用。
将self—Attention替换相应的GRU或者RNN,就能实现从输出a到输出b,每一个b都能看到a1-a4的信息,同时b的计算还能实现并行化。
Self-Attention就是来自于《Attention is all you need》这篇文献当中,可以通过下面的链接进行下载:
https://arxiv.org/abs/1706.03762
1.1 Self-Attention解决方案
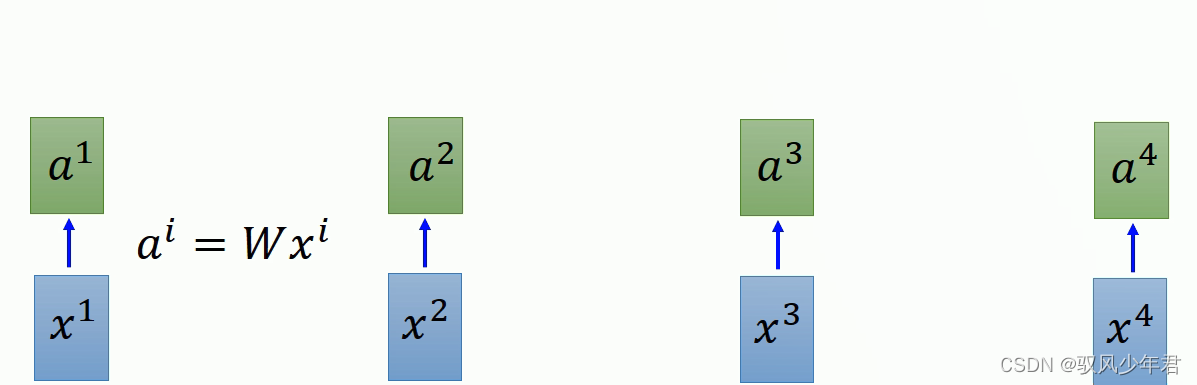
如图相应的X是作为输入,每一个输入x都乘以一个权重W,得到αi。
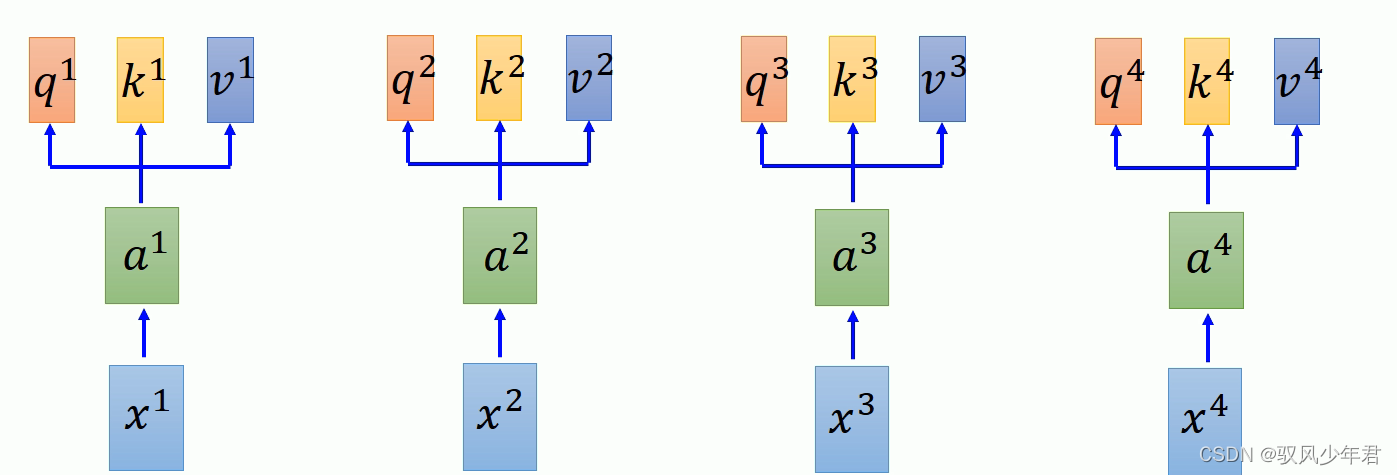
然后将每一个α都拆分为三个向量,q,k,v的三个。qk主要完成Attention的工作,v完成抽取序列信息。
Q:其中q用于去与其他向量进行匹配计算
K:是用于被匹配计算的向量
V:用于抽取相应序列的信息
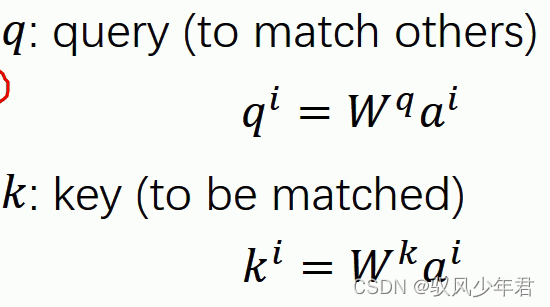
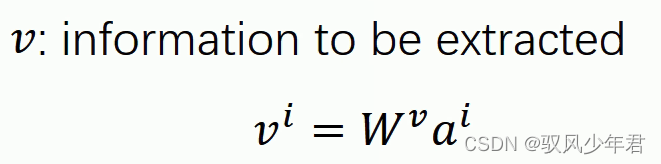
拿每个queryq去对每个key k做attention
主动用当前的Q,与自己和其他输出的k进行attention计算

qk做点乘,其中还除去维度d,d是q、k的维度。

其中做完相应的Attention后还需要,进行softmax,获取相应的α帽。就是注意力的分布
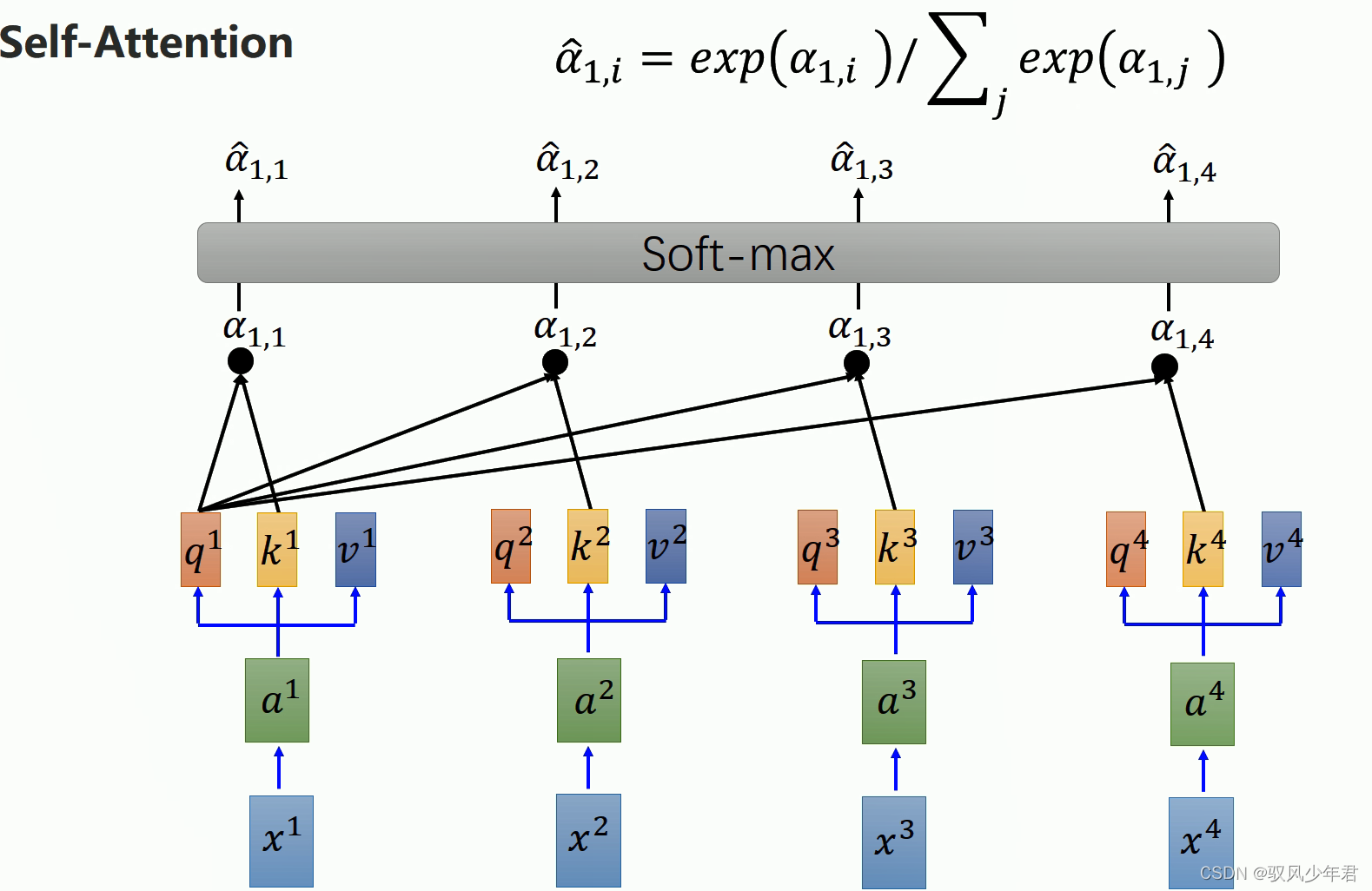
而b,是当前的q计算得到的attention值α与每个输入的v进行相互乘,并且累加得到,获取到了当前时刻所有输入数据的信息。同理得到b2
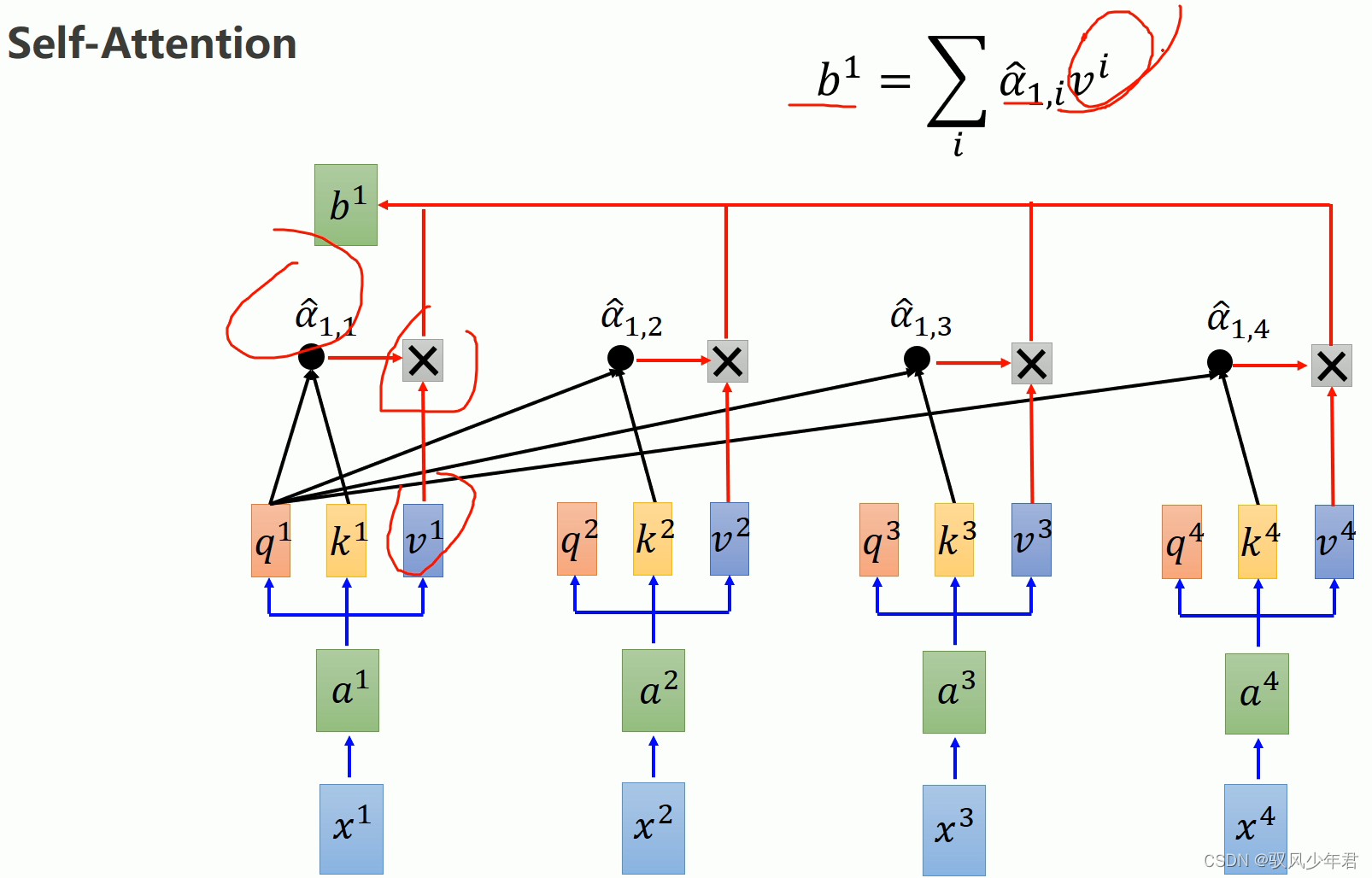
同理得到a2、b2,是当前的q2与其他的k、与其他的v计算分别得到attention值和序列信息值。

1.2 总结
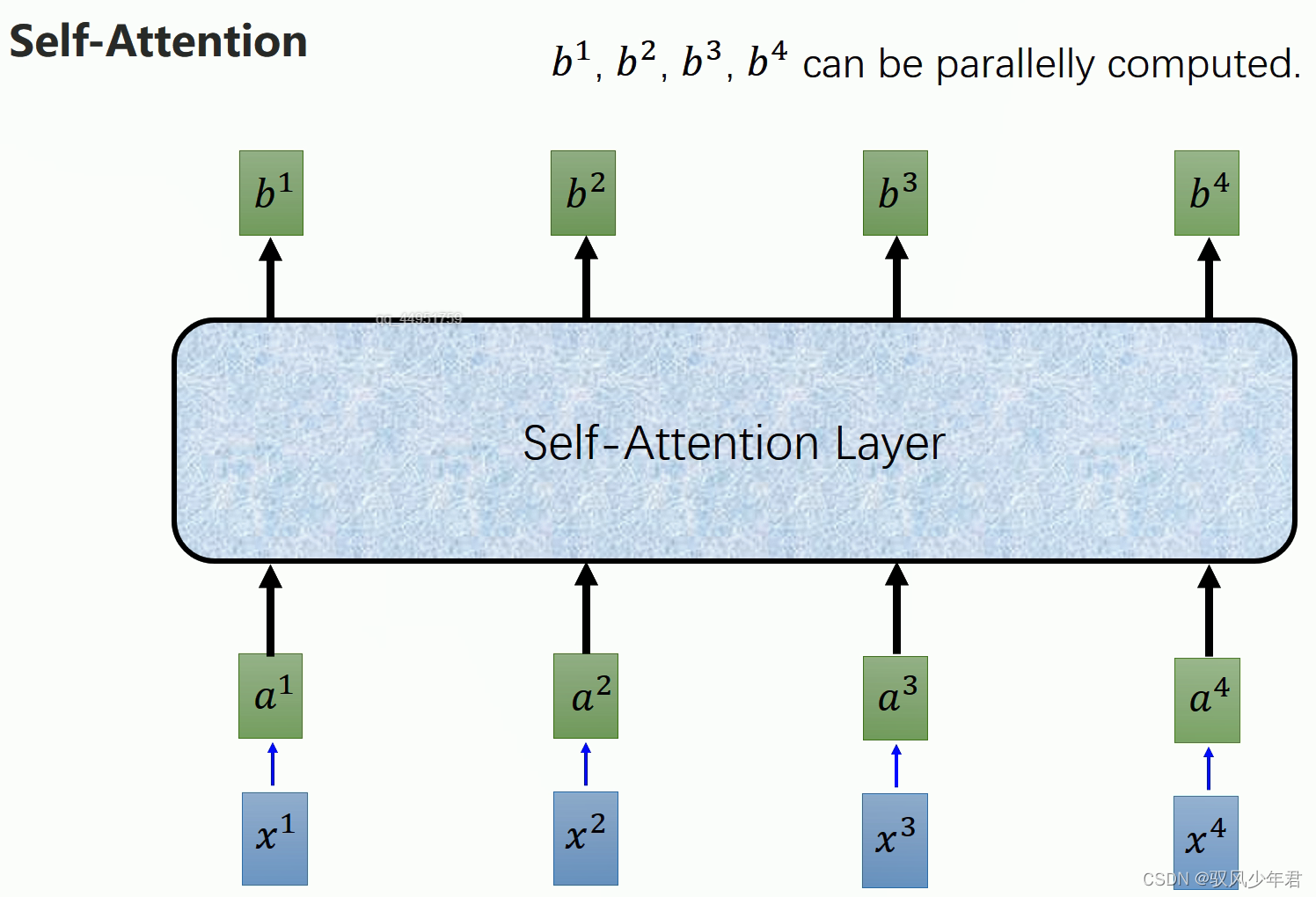
因为每个值阿尔法,都是分别计算得到的,所以不需要依靠计算上一个节点。
并且通过分出三个向量,实现对于每个节点的信息的运用。
2. Self-Attention的数学理论基础
对于每一个输入的x,都可以经过一个相应的矩阵W的计算,得到相应的q,k,v。
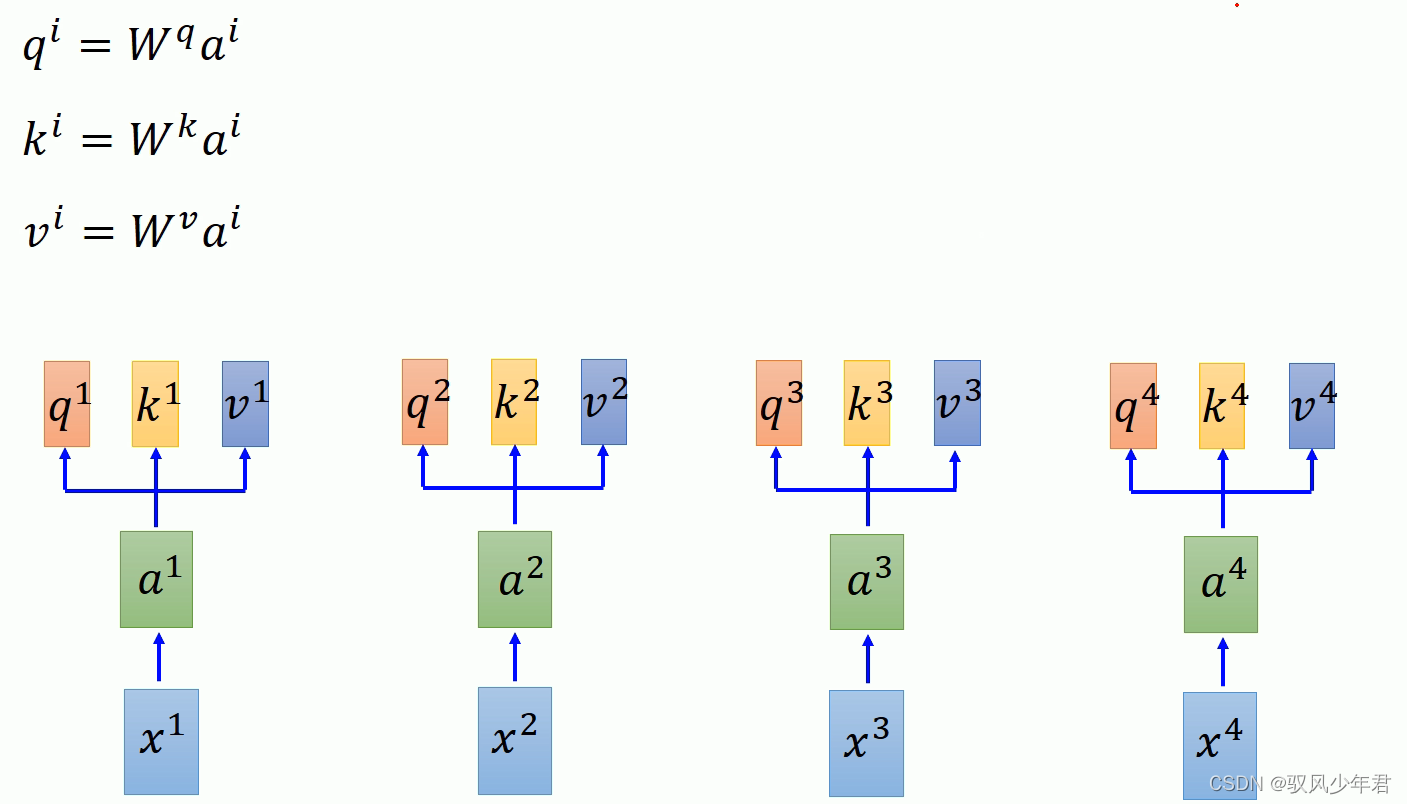
其中对于每个的a进行拼接向量,得到I矩阵,乘以相应的W,就得到Q矩阵。

同理得到相应的K矩阵

同理得到相应的V矩阵

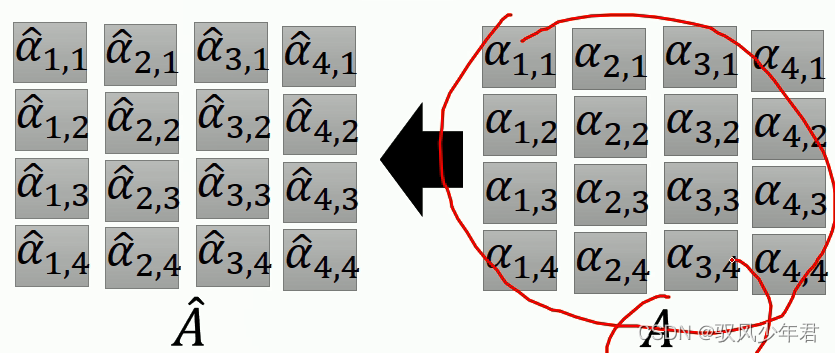
相应的A帽矩阵,如下所示,是根据相应的A矩阵softma变换得到Attention

所以A矩阵就是为K矩阵与Q矩阵变换得到

将得到的A矩阵进行Softmax计算得到相应的A帽矩阵
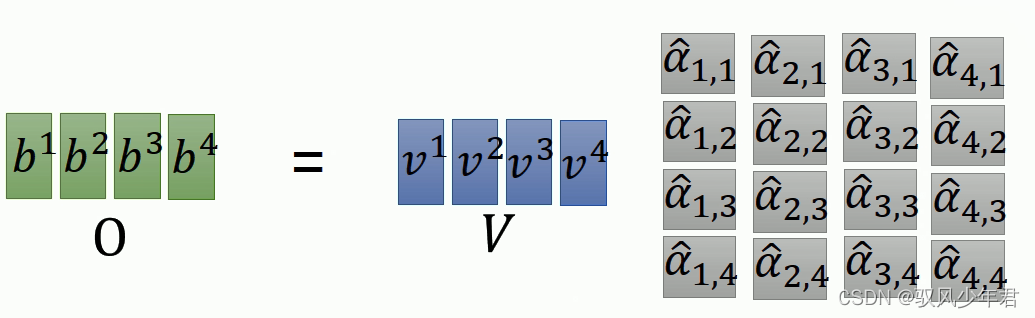
B帽矩阵 = A帽矩阵* V矩阵
所以相应的Self-Attention就是相应的矩阵的变换得到,输入的数据为I矩阵,经过W矩阵得到相应的QKV矩阵
K矩阵转置,与Q矩阵计算得到A矩阵,A矩阵归一化后得到Attention
将Attention后的结果乘以V,就得到了序列化的数据矩阵O,作为输出。

3. Multi-Head-self Attention(多头自注意力模型)
下面主要演示双头的注意力模型,一般来说都是选用偶数头
多头,一般就是将相应的QKV进行拆分,拆分成相应的几头
多头的注意力模型,可以更加细节的发现局部的信息。所以可以解决局部信息,如果更加看重局部信息的时候,多头的模型就是比较合适的。

4 Transform
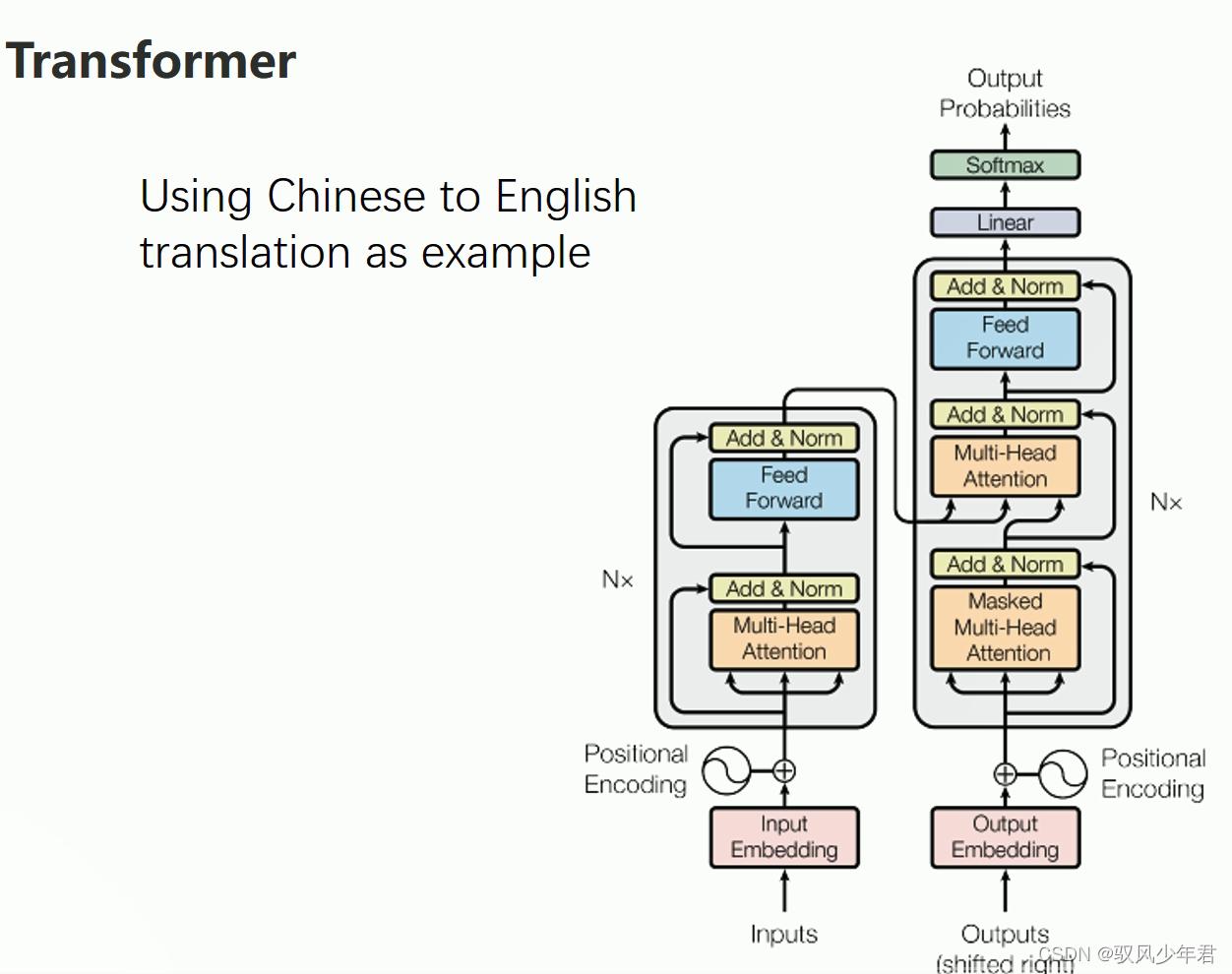
.
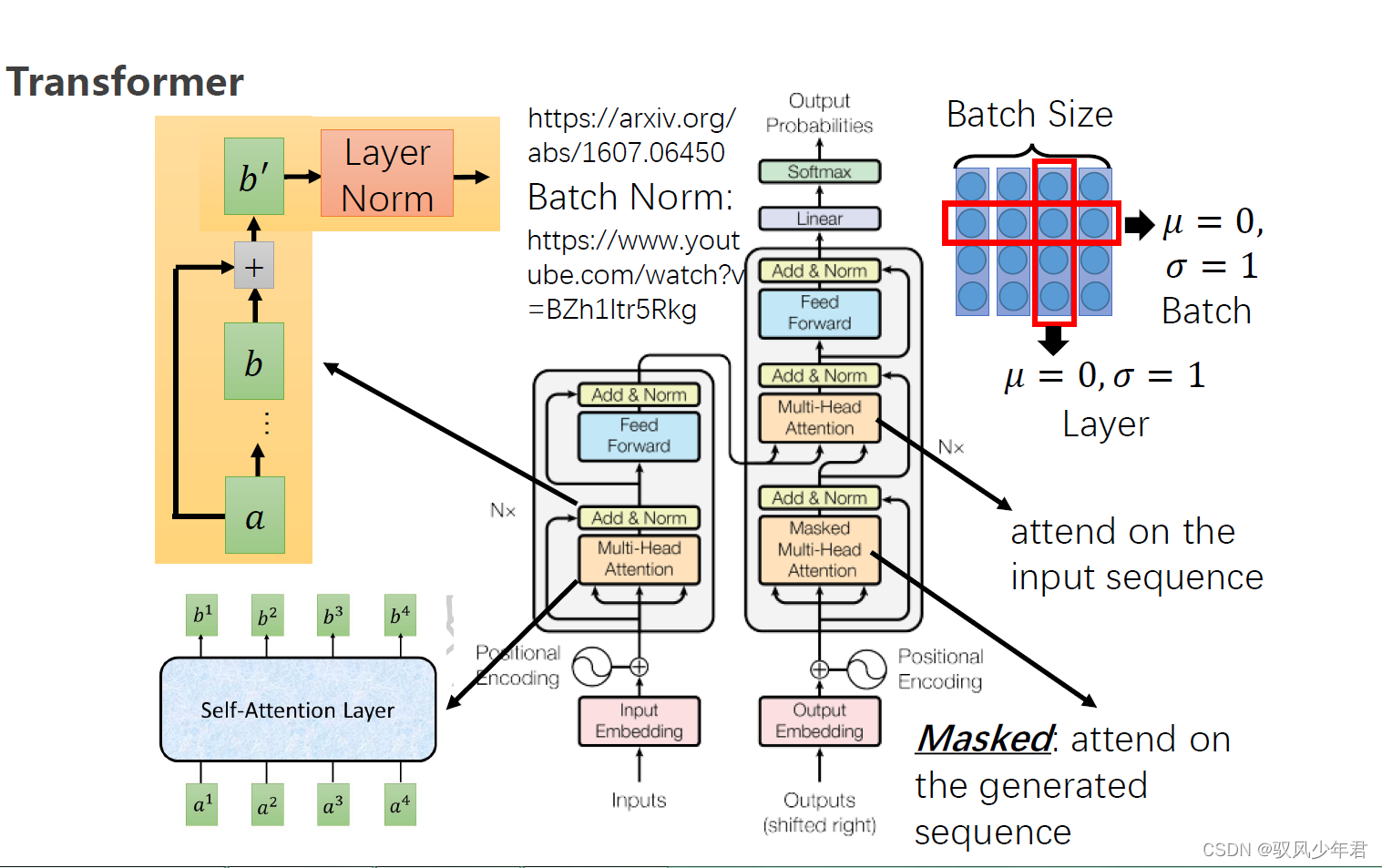
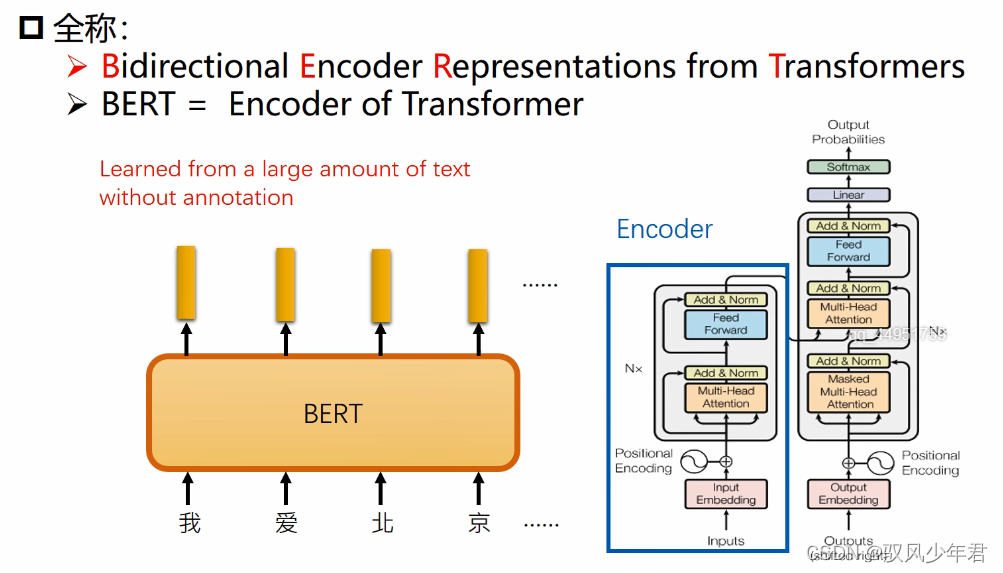
5.Bert理论基础
这篇关于【Self-Attention——Transform—Bert】相关的基础理论的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






