《neural network and deep learning》题解——ch03 如何选择神经网络的超参数

本文主要是介绍《neural network and deep learning》题解——ch03 如何选择神经网络的超参数，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

http://blog.csdn.net/u011239443/article/details/77748116

问题一

上一节有问题也是调参，我们在这里讲解：

更改上面的代码来实现 L1 规范化,使用 L1 规范化使用 30 个隐藏元的神经网络对 MNIST数字进行分类。你能够找到一个规范化参数使得比无规范化效果更好么?

如何修改代码可参阅上节：http://blog.csdn.net/u011239443/article/details/77649026#t5

当无规范化时，我们将上节的代码update_mini_batch中做修改：

self.weights = [w - (eta / len(mini_batch)) * nw for w, nw inzip(self.weights, nabla_w)]

total_cost中去掉：

cost += 0.5 * (lmbda / len(data)) * sum(np.linalg.norm(w) ** 2 for w in self.weights)

为了加快我们的训练，我们使得将训练集设置为1000，验证集设置为100：

net.SGD(training_data[:1000],30,10,0.5,evaluation_data=validation_data[:100],monitor_evaluation_accuracy=True)

结果：

Epoch 30 training complete
Acc on evaluation: 17 / 100

加入 L1 ， λ = 100.0 时，结果：

Epoch 30 training complete
Acc on evaluation: 11 / 100

λ = 10.0 时，结果：

Epoch 29 training complete
Acc on evaluation: 11 / 100

λ = 1.0 时，结果：

Epoch 30 training complete
Acc on evaluation: 31 / 100

所以当λ = 1.0 时使，可以使得比无规范化效果更好。

问题二

修改 network2.py 来实现提前终止,并让 n 回合不提升终止策略中的 n 称为可以设置的参数。

随机梯度函数多加一个参数max_try：

    def SGD(self, training_data, epochs, mini_batch_size, eta,lmbda=0.0,evaluation_data=None,monitor_evaluation_cost=False,monitor_evaluation_accuracy=False,monitor_training_cost=False,monitor_training_accuray=False,max_try = 100):

cnt 记录不提升的次数，如达到max_try，就退出循环。这里用monitor_evaluation_accuracy举例：

        cnt = 0for j in xrange(epochs):......if monitor_evaluation_accuracy:acc = self.accuracy(evaluation_data)evaluation_accurary.append(acc)if len(evaluation_accurary) > 1 and acc < evaluation_accurary[len(evaluation_accurary)-2]:cnt += 1if cnt >= max_try:breakelse:cnt = 0print "Acc on evaluation: {} / {}".format(acc, n_data)......

问题三

你能够想出不同于 n 回合不提升终止策略的其他提前终止策略么?理想中,规则应该能够获得更高的验证准确率而不需要训练太久。将你的想法实现在 network2.py 中,运行这些实验和 3 回合（10 回合太多，基本上训练全部，所以改成 3）不提升终止策略比较对应的验证准确率和训练的回合数。

策略与实现

多一个参数x，当提升率小于x，则停止。

随机梯度函数多加一个参数max_x：

    def SGD(self, training_data, epochs, mini_batch_size, eta,lmbda=0.0,evaluation_data=None,monitor_evaluation_cost=False,monitor_evaluation_accuracy=False,monitor_training_cost=False,monitor_training_accuray=False,min_x = 0.01):

当提升率小于x，则停止。这里用monitor_evaluation_accuracy举例：

            if monitor_evaluation_accuracy:acc = self.accuracy(evaluation_data)evaluation_accurary.append(acc)if len(evaluation_accurary) > 1 and \(acc - evaluation_accurary[len(evaluation_accurary)-2])*1.0/(1.0*n_data) < min_x:breakprint "Acc on evaluation: {} / {}".format(acc, n_data)

对比

10 回合不提升终止策略：

net.SGD(training_data[:1000],50,10,0.25,5.0,evaluation_data=validation_data[:100],monitor_evaluation_accuracy=True,max_try=3)

的结果：

Epoch 32 training complete
Acc on evaluation: 15 / 100

提升率小于x停止策略：

Epoch 3 training complete
Acc on evaluation: 17 / 100

问题四

更改 network2.py 实现学习规则:每次验证准确率满足满足 10 回合不提升终止策略时改变学习速率;当学习速率降到初始值的 1/128 时终止。

对问题二中的代码进行稍微的修改，128 = 2 ^ 7 。所以，多加个计数 del_cnt 记录学习率减小的次数：

        cnt = 0del_cnt = 0for j in xrange(epochs):......if monitor_evaluation_accuracy:acc = self.accuracy(evaluation_data)evaluation_accurary.append(acc)if len(evaluation_accurary) > 1 and acc < evaluation_accurary[len(evaluation_accurary)-2]:cnt += 1if cnt >= max_try:del_cnt += 1if del_cnt >= 7:breaketa /= 2.0cnt = 0   else:cnt = 0print "Acc on evaluation: {} / {}".format(acc, n_data)

问题五

使用梯度下降来尝试学习好的超参数的值其实很受期待。你可以想像关于使用梯度下降来确定 λ 的障碍么?你能够想象关于使用梯度下降来确定 η 的障碍么?

• 使用梯度下降来确定 λ 的障碍在于，
  
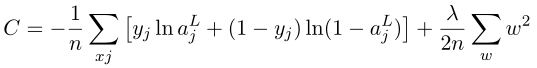
  得：
  $ \frac{∂C}{∂λ} = \frac{\sum_ww^2}{2n} = 0$
  最优化目标使得 w = 0，但是 w 也是我们原来需要优化的。

• 使用梯度下降来确定 η 的障碍在于，η 的最优解不是一个常数，随着迭代次数的增加，η 的最优解会越来越小。

这篇关于《neural network and deep learning》题解——ch03 如何选择神经网络的超参数的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---