《搜索和推荐中的深度匹配》——2.4 推荐中的潜在空间模型

本文主要是介绍《搜索和推荐中的深度匹配》——2.4 推荐中的潜在空间模型，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

重磅推荐专栏：《Transformers自然语言处理系列教程》
手把手带你深入实践Transformers，轻松构建属于自己的NLP智能应用！

接下来，我们简要介绍在潜在空间中执行匹配的代表性推荐方法，包括偏置矩阵分解 (BMF)【1】、Factored Item Similarity Model (FISM) 【2】和分解机 (FM)【3】。

参阅《深度推荐模型——FM》

2.4.1 有偏矩阵分解

偏置矩阵分解 (BMF) 是一种用于预测用户评分的模型【1】，即将推荐形式化为回归任务。它是在 Netflix Challenge 期间开发的，由于其简单性和有效性而迅速流行起来。匹配模型可以表述为：
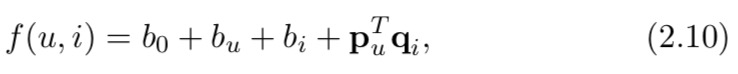
在这里插入图片描述
其中 $b_0、b_u 和 b_i$ 是标量，表示评分中的总体偏差、用户偏差和项目偏差，而 $p_u 和 q_i$ 是表示用户和项目的潜在向量。这可以解释为仅使用用户和项目的 ID 作为它们的特征，并使用两个线性函数将 ID 投影到潜在空间中。设 u 为用户 u 的 one-hot ID 向量，i 为 item i 的 one-hot ID 向量，P 为用户投影矩阵，Q 为 item 投影矩阵。那么我们可以在方程（2.4）的映射框架下表达模型：
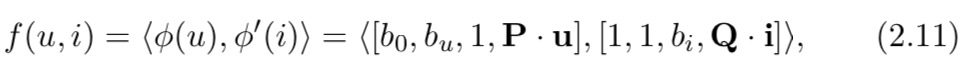
在这里插入图片描述
其中 [·, ·] 表示向量连接。
给定训练数据，学习模型参数 $Θ = {b0,bu,bi,P,Q})$ 通过正则化优化逐点回归误差：

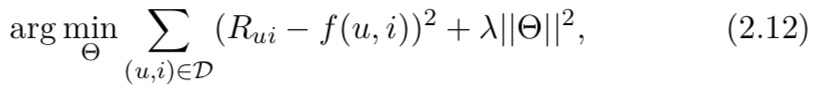
其中 D 表示所有观察到的评分， $R_{ui}$ 表示 (u, i) 的评分，λ 是 L2 正则化系数。由于它是一个非凸优化问题，因此通常采用交替最小二乘法【4】或随机梯度下降法【5】，这不能保证找到全局最优解。

参阅《深入理解Spark ML：基于ALS矩阵分解的协同过滤算法与源码分析》

2.4.2 因子项相似度模型

Factored Item Similarity Model (FISM) 【2】采用基于项目的协同过滤假设，即用户会更喜欢与他们目前选择的项目相似的项目。为此，FISM 使用用户选择的项目来代表用户，并将组合项目投影到潜在空间中。 FISM 的模型公式为：
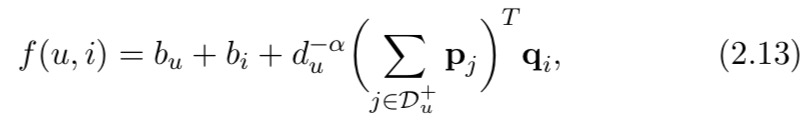
在这里插入图片描述
其中 $D_u^+$ 表示用户 u 选择的项目， $d_u$ 表示此类项目的数量， $d^{−α}$ 表示跨用户的归一化。 $q_i$ 是目标物品 i 的潜在向量， $p_j$ 是用户 u 选择的历史物品 j 的潜在向量。FISM 将 $p^T_j q_j$ 视为项目 i 和 j 之间的相似度，并聚合目标项目 i 和用户 u 的历史项目的相似度。

FISM 采用成对损失并从二元隐式反馈中学习模型。设 U 为所有用户，总成对损失由下式给出
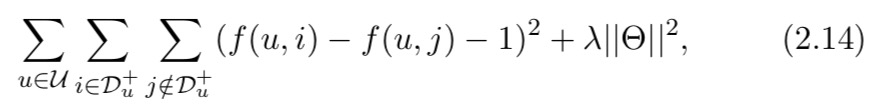
在这里插入图片描述
这迫使正（观察到的）实例的分数大于负（未观察到的）实例的分数，边距为 1。另一种成对损失，贝叶斯个性化排名 (BPR)【6】损失也被广泛使用：

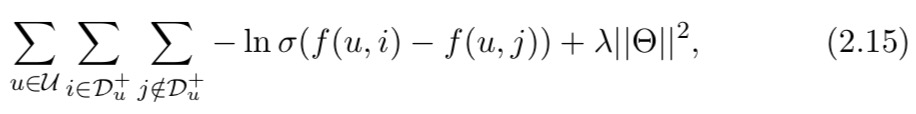
其中 σ(·) 表示 sigmoid 函数，它将分数的差异转换为介于 0 和 1 之间的概率值，因此损失具有概率解释。两种损失之间的主要区别在于，BPR 将正例和负例之间的差异强制尽可能大，而没有明确定义余量。这两个成对损失都可以看作是 AUC 指标的替代品，该指标衡量模型正确排序了多少对项目

2.4.3 分解机

Factorization Machine (FM) 【3】是作为推荐的通用模型而开发的。除了用户和物品之间的交互信息，FM还结合了用户和物品的边信息，例如用户资料（例如年龄、性别等）、物品属性（例如类别、标签等）和上下文（例如，时间、地点等）。 FM 的输入是一个特征向量 x = [x1, x2, … . . , xn] 可以包含用于表示匹配函数的任何特征，如上所述。因此，FM 将匹配问题视为监督学习问题。它将特征投影到潜在空间中，对它们与内积的相互作用进行建模：
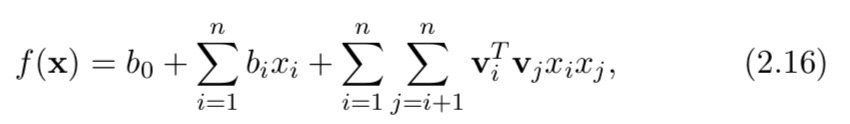
在这里插入图片描述
其中 $b_0$ 是偏差， $b_i$ 是特征 $x_i$ 的权重， $v_i$ 是特征 $x_i$ 的潜在向量。鉴于输入向量 x 可能很大但很稀疏，例如分类特征的多热编码，FM 仅捕获非零特征之间的交互（使用项 $x_ix_j$ ）。

FM 是一个非常通用的模型，因为将不同的输入特征输入模型将导致模型的不同公式。例如，当x只保留用户ID和目标物品ID时，FM就变成了BMF模型；当 x 只保留用户历史选择项目的 ID 和目标项目 ID 时，FM 成为 FISM 模型。其他流行的潜在空间模型，例如 SVD++【7】和因子化个性化马尔可夫链（FPMC）【8】也可以通过适当的特征工程归入 FM。

引文

【1】Koren, Y., R. Bell, and C. Volinsky (2009). “Matrix factorization tech- niques for recommender systems”. Computer. 42(8): 30–37.
【2】Kabbur, S., X. Ning, and G. Karypis (2013). “FISM: Factored item similarity models for top-N recommender systems”. In: Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. KDD ’13. Chicago, IL, USA: ACM. 659–667.
【3】Rendle, S. (2010). “Factorization machines”. In: Proceedings of the
2010 IEEE International Conference on Data Mining. ICDM ’10.
Washington, DC, USA: IEEE Computer Society. 995–1000.
【4】He, X., H. Zhang, M.-Y. Kan, and T.-S. Chua (2016b). “Fast matrix factorization for online recommendation with implicit feedback”. In: Proceedings of the 39th International ACM SIGIR Conference
on Research and Development in Information Retrieval. SIGIR ’16.
Pisa, Italy: ACM. 549–558.
【5】Koren, Y., R. Bell, and C. Volinsky (2009). “Matrix factorization tech- niques for recommender systems”. Computer. 42(8): 30–37.
【6】Rendle, S., C. Freudenthaler, Z. Gantner, and L. Schmidt-Thieme
(2009). “BPR: Bayesian personalized ranking from implicit feedback”. In: Proceedings of the Twenty-Fifth Conference on Uncertainty in Artificial Intelligence. UAI ’09. Montreal, Quebec, Canada: AUAI Press. 452–461. url: http://dl.acm.org/citation.cfm?id=1795114.1 795167.
【7】Koren, Y. (2008). “Factorization meets the neighborhood: A multi- faceted collaborative filtering model”. In: Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. KDD ’08. Las Vegas, NV, USA: ACM. 426–434.
【8】Rendle, S., C. Freudenthaler, and L. Schmidt-Thieme (2010). “Factoriz- ing personalized Markov chains for next-basket recommendation”. In: Proceedings of the 19th International Conference on World Wide
Web. WWW ’10. Raleigh, NC, USA: ACM. 811–820.

这篇关于《搜索和推荐中的深度匹配》——2.4 推荐中的潜在空间模型的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！