OpenCV学习基础图像操作（十五）：频域变换及相关操作

本文主要是介绍OpenCV学习基础图像操作（十五）：频域变换及相关操作，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

基础原理

图像的频域处理提供了一种强大的工具，用于分析和处理图像的频率成分。傅里叶变换、小波变换和Gabor变换等技术各有优劣，适用于不同的应用场景。通过选择合适的频域算法，可以实现图像的压缩、去噪、特征提取和增强等多种应用。本篇主要针对常见的傅里叶变换和小波变换来进行介绍.

DFT 离散傅里叶变换

离散傅里叶变换（英语：Discrete Fourier Transform，缩写为DFT），是傅里叶变换在时域和频域上都呈离散的形式，将信号的时域采样变换为其DTFT的频域采样。

在形式上，变换两端（时域和频域上）的序列是有限长的，而实际上这两组序列都应当被认为是离散周期信号的主值序列。即使对有限长的离散信号作DFT，也应当将其看作其周期延拓的变换。在实际应用中通常采用快速傅里叶变换计算DFT。

对于 $N$ 点序列 ${x[n]}_{0\leq n < N}$ ，它的离散傅里叶变换（DFT）为

$\widehat{x}[k]=\sum_{n=0}^{N-1}e^{-i\frac{2\pi }{N}nk}x[n] \ \ \ k = 0,1, ...,N-1$

其中 $e$ 是自然对数的底数， $i$ 是虚数单位。通常以符号 $\mathfrak{F}$ 表示这一变换，即

$\widehat{x}=\mathfrak{F}x$

离散傅里叶变换的逆变换（IDFT）为：

$x[k]=\sum_{k=0}^{N-1}e^{i\frac{2\pi }{N}nk}\widehat{x}[n] \ \ \ n = 0,1, ...,N-1$

可以记为：

$x=\mathfrak{F}^{-1}\widehat{x}$

实际上，DFT和IDFT变换式中和式前面的归一化系数并不重要。在上面的定义中，DFT和IDFT前的系数分别为1和 $\frac{1}{N}$ 。有时会将这两个系数都改成 $\frac{1}{\sqrt{N}}$ 。

从公式来看,离散傅立叶变换是将图像拆分到不同频率的信号上观察,但是只能观察到整幅图像整体在频域的分布,完全丢弃了时域上的信息,则可能比较不直观.

WT 小波变换

小波变换使用一系列的不同尺度的小波去分解原函数，变换后得到的是原函数在不同尺度小波下的系数。不同的小波通过平移与尺度变换分解，平移是为了得到原函数的时间特性，尺度变换是为了得到原函数的频率特性。

小波变换步骤：

把小波w(t)和原函数f(t)的开始部分进行比较，计算系数C。系数C表示该部分函数与小波的相似程度。
把小波向右移k单位，得到小波w(t-k)，重复1。重复该步骤直至函数f结束.
扩展小波w(t)，得到小波w(t/2)，重复步骤1,2.
不断扩展小波，重复1,2,3.

相比离散傅立叶变换,小波变换是用一个局部的频域响应子来与图像进行卷积,最后得到是在不同局部位置上的对不同频率的响应强度.

API介绍

DFT

将一张图转换到频域内,再分别通过低通滤波和高通滤波,观察到低通滤波后,图像保存了更多的整体轮廓,而高通滤波后,图像保存了更多的边界处的细节.其中靠近图像中央的是低频区,远离中央的是高频区,亮度代表的是幅度,方向代表的是相位.

import cv2
import numpy as np
import matplotlib.pyplot as plt# 读取图像并转换为灰度图像
img = cv2.imread('lena.jpg', cv2.IMREAD_GRAYSCALE)# 获取图像的行列数
rows, cols = img.shape
nrows = cv2.getOptimalDFTSize(rows)
ncols = cv2.getOptimalDFTSize(cols)
right = ncols - cols
bottom = nrows - rows
padded = cv2.copyMakeBorder(img, 0, bottom, 0, right, cv2.BORDER_CONSTANT, value=0)# 执行傅里叶变换
dft = cv2.dft(np.float32(padded), flags=cv2.DFT_COMPLEX_OUTPUT)
dft_shift = np.fft.fftshift(dft)# 计算幅值谱
magnitude_spectrum = 20 * np.log(cv2.magnitude(dft_shift[:, :, 0], dft_shift[:, :, 1]))# 创建掩膜，高频保留，低频设置为0
rows, cols = dft_shift.shape[:2]
crow, ccol = rows // 2 , cols // 2
mask = np.ones((rows, cols, 2), np.uint8)
r = 30  # 设置高通滤波器半径
center = [crow, ccol]
x, y = np.ogrid[:rows, :cols]
mask_area = (x - center[0])**2 + (y - center[1])**2 <= r*r
mask[mask_area] = 0# 应用掩膜并进行逆DFT
fshift = dft_shift * mask
f_ishift = np.fft.ifftshift(fshift)
img_back_H = cv2.idft(f_ishift)
img_back_H = cv2.magnitude(img_back_H[:, :, 0], img_back_H[:, :, 1])# 创建掩膜，低频保留，高频设置为0
mask = np.zeros((rows, cols, 2), np.uint8)
mask[mask_area] = 1# 应用掩膜并进行逆DFT
fshift = dft_shift * mask
f_ishift = np.fft.ifftshift(fshift)
img_back_L = cv2.idft(f_ishift)
img_back_L = cv2.magnitude(img_back_L[:, :, 0], img_back_L[:, :, 1])# 显示滤波后的图像
plt.subplot(221), plt.imshow(img, cmap='gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(222), plt.imshow(magnitude_spectrum, cmap='gray')
plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
plt.subplot(223), plt.imshow(img_back_L, cmap='gray')
plt.title('Low Pass Filtered Image'), plt.xticks([]), plt.yticks([])
plt.subplot(224), plt.imshow(img_back_H, cmap='gray')
plt.title('High Pass Filtered Image'), plt.xticks([]), plt.yticks([])
plt.show()

WT

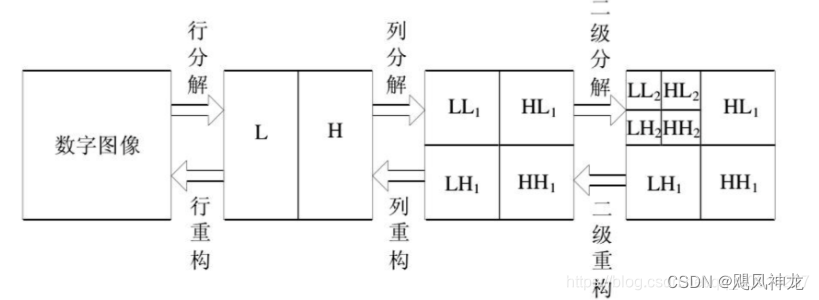
分解过程可描述为：首先对图像的每一行进行 1D-DWT，获得原始图像在水平方向上的低频分量 L 和高频分量 H，然后对变换所得数据的每一列进行 1D-DWT，获得原始图像在水平和垂直方向上的低频分量 LL、水平方向上的低频和垂直方向上的高频 LH、水平方向上的高频和垂直方向上的低频 HL 以及水平和垂直方向上的的高频分量 HH。

import cv2
import pywt
import numpy as np
import matplotlib.pyplot as plt# 读取图像并转换为灰度图像
img = cv2.imread('1.png', cv2.IMREAD_GRAYSCALE)# 选择小波函数
wavelet = 'haar'# 进行二维离散小波变换
coeffs2 = pywt.dwt2(img, wavelet)# 提取系数
LL, (LH, HL, HH) = coeffs2# 显示小波系数图像
plt.figure(figsize=(12, 12))
titles = ['Approximation', 'Horizontal detail', 'Vertical detail', 'Diagonal detail']images = [LL, LH, HL, HH]
for i, (title, image) in enumerate(zip(titles, images)):plt.subplot(2, 2, i + 1)plt.imshow(image, cmap='gray')plt.title(title)plt.axis('off')
plt.show()