C语言数据结构堆排序、向上调整和向下调整的时间复杂度的计算、TopK问题等的介绍

本文主要是介绍C语言数据结构堆排序、向上调整和向下调整的时间复杂度的计算、TopK问题等的介绍，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

---

前言

C语言数据结构堆排序、向上调整和向下调整的时间复杂度的计算、TopK问题等的介绍

---

一、堆排序

排列一个一维数组，可以通过两个步骤进行排序。

1. 建堆（大根堆或小根堆）
2. 堆排序（通过向下或者向上调整排序）’

需要注意的是 堆排序排升序则建大堆，排降序则建小堆。

1. 排升序

（1）. 建堆

这里建堆采用向下调整建堆，因为向上调整建堆的时间复杂度比向下调整建堆的时间复杂度大。可参考二。

• 向下调整建堆，从最后一个叶子节点的父节点开始调整。

// 向下调整 按大根堆调整
void AdjustDown(HPDataType* a, int n ,int parent)
{int child = parent * 2 + 1;while (child < n){// 判断左右子树的根谁大 并防止越界if (child+ 1 < n && a[child] < a[child + 1]){child++;}if (a[child] > a[parent]){Swap(&a[parent], &a[child]);parent = child;child = parent * 2 + 1;}else{break;}}
}// 排升序 建大堆
void HeapSort(int* arr, int n)
{int i = 0;// 建堆---向下调整建堆for (i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(arr, n, i);}
}

• （n-1）是找到最后一个叶子节点，(n-1-1)/2找到最后一个叶子节点的双亲节点，然后向下调整。

（2）. 排序

• 排序的思想：
  和删除堆顶的元素的思想一样。

1. 已经建好了大堆，所以先交换根元素和最后一个叶子节点元素。此时最后一个叶子节点是最大值。
2. 将此时除了最后一个叶子节点元素看成一个堆，并将此时的根元素向下调整。
3. 再继续交换根元素和此时最后一个叶子结点元素，重复以上过程。即可达到排序效果。

// 排升序 建大堆
void HeapSort(int* arr, int n)
{int i = 0;// 建堆---向下调整建堆for (i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(arr, n, i);}// 排序int end = n - 1;while (end > 0){Swap(&arr[0], &arr[end]);AdjustDown(arr, end, 0);end--;}
}int main()
{int arr[10] = { 2,3,1,9,5,7,8,6,4, 0 };HeapSort(arr, 10);int i = 0;for (i = 0; i < 10; i++){printf("%d ", arr[i]);}printf("\n");return 0;
}

效果如下：

2. 拍降序

（1）. 建堆

• 排降序，建小堆
• 向下调整建小堆，向下调整的时间复杂度比向上调整时间复杂度低

// 向下调整 按小根堆调整
void AdjustDown(HPDataType* a, int n ,int parent)
{int child = parent * 2 + 1;while (child < n){// 判断左右子树的根谁小 并防止越界if (child+ 1 < n && a[child] > a[child + 1]){child++;}if (a[child] < a[parent]){Swap(&a[parent], &a[child]);parent = child;child = parent * 2 + 1;}else{break;}}
}// 拍降序，建小堆
void HeapSort(int* arr, int n)
{int i = 0;for (i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(arr, n, i);}
}

（2）. 排序

• 排序的思想：
  和删除堆顶的元素的思想一样。

1. 已经建好了小堆，所以先交换根元素和最后一个叶子节点元素。此时最后一个叶子节点是最小值。
2. 将此时除了最后一个叶子节点元素看成一个堆，并将此时的根元素向下调整。
3. 再继续交换根元素和此时最后一个叶子结点元素，重复以上过程。即可达到排序效果。

// 拍降序，建小堆
void HeapSort(int* arr, int n)
{int i = 0;// 建堆---- 向下调整建堆for (i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(arr, n, i);}// 排序int end = n - 1;while (end > 0){Swap(&arr[0], &arr[end]);AdjustDown(arr, end, 0);end--;}}int main()
{int arr[10] = { 2,3,1,9,5,7,8,6,4, 0 };HeapSort(arr, 10);int i = 0;for (i = 0; i < 10; i++){printf("%d ", arr[i]);}printf("\n");return 0;
}

效果如下：

注意拍升序和拍降序的向下调整函数是不一样的

二、建堆时间复杂度的计算

• 建堆事实上是模拟堆中插入数据，并向上或向下调整。
• 所以建堆时间复杂度的计算本质上是向上或者向下调整的时间复杂度

注意： 堆是完全二叉树，这里用满二叉树来近似计算，因为时间复杂度计算的是量级，多或少节点不影响。

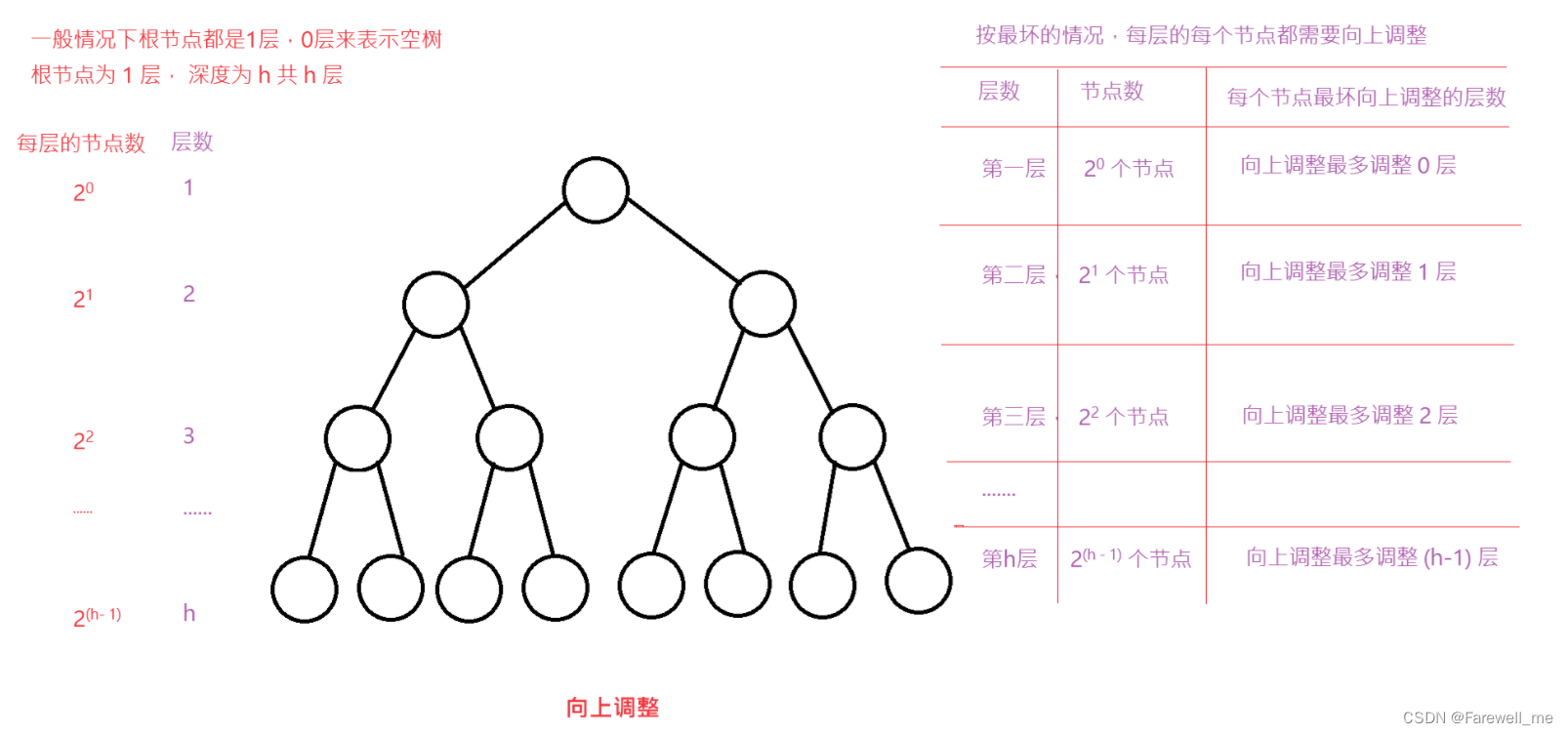
1. 向上调整时间复杂度

见图示：
1.

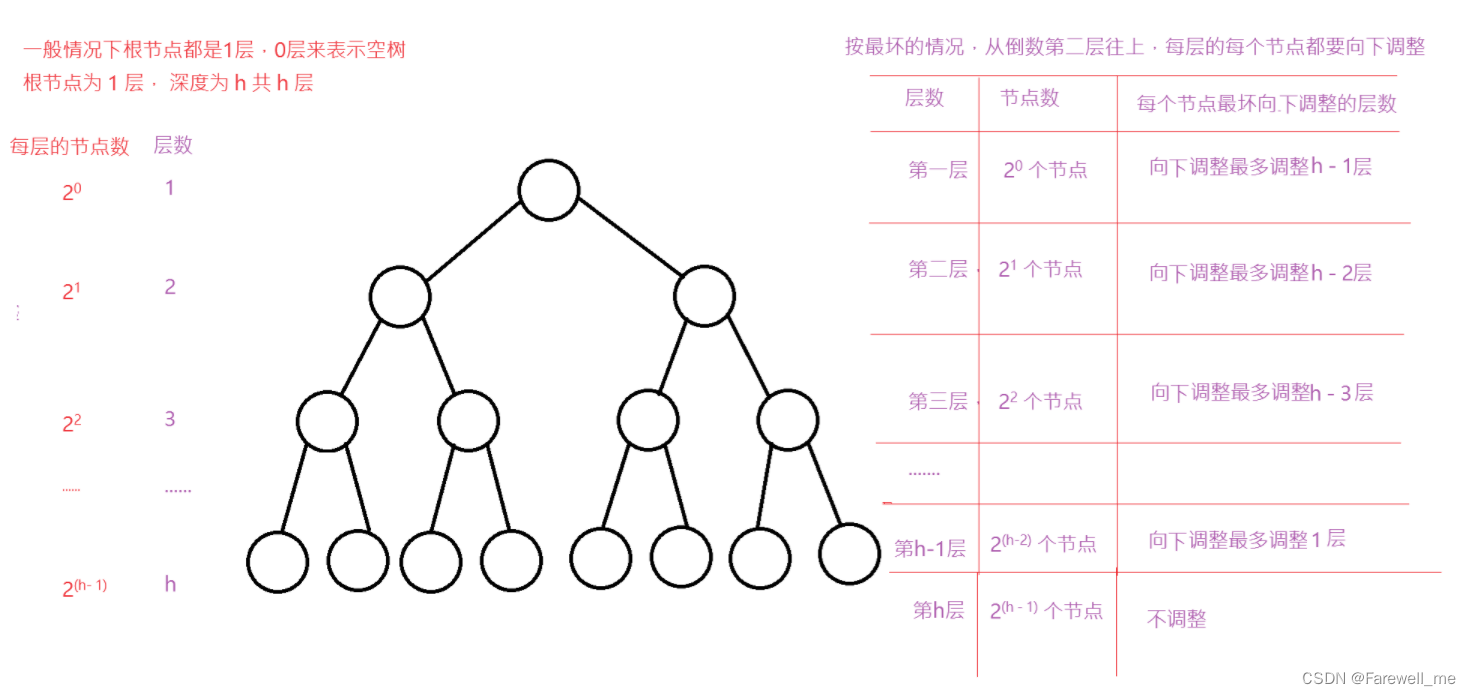
2. 向下调整时间复杂度

见图示：
1.

三、TopK问题

在非常大的数字中找到前K个

• 由于没有数据，先随机生成10000个数据写入文件中
• 然后建K个数据的小堆
• 剩余n-k个数据依次与小堆根元素比较，若大于根元素则入堆，并向下调整，若不大于根元素，则继续找下一个，知道文件读完。

void PrintfTopK(const char* file, int k)
{int* topk = (int*)malloc(sizeof(int)* k);if (topk == NULL){perror("PrintfTopK malloc");return;}// 以读的形式打开文件FILE* pfout = fopen(file, "r");if (pfout == NULL){perror("PrintfTopK fopen");return;}int i = 0;// 读出前K个数for (i = 0; i < k; i++){fscanf(pfout, "%d", &topk[i]);}// 建堆for (i = (k - 1 - 1) / 2; i >= 0; i--){AdjustDown(topk, k, i);}// 剩余n - k 个数分别于根元素比较int val = 0;int ret = fscanf(pfout, "%d", &val);while (ret != EOF){if (val > topk[0]){topk[0] = val;AdjustDown(topk, k, 0);}ret = fscanf(pfout, "%d", &val);}for (i = 0; i < k; i++){printf("%d ", topk[i]);}free(topk);fclose(pfout);
}void CreateNData()
{int n = 10000;const char* file = "data.txt";FILE* pfin = fopen(file, "w");if (pfin == NULL){perror("TestTopK fopen");return;}int i = 0;for (i = 0; i < n; i++){int x = rand() % 10000;fprintf(pfin, "%d\n", x);}fclose(pfin);
}int main()
{srand((unsigned int)time(NULL));CreateNData();PrintfTopK("data.txt", 10);return 0;
}

• 其中的向下调整都是按小根堆向下调整。可参考一、二内容

---

效果如下：

---

总结

C语言数据结构堆排序、向上调整和向下调整的时间复杂度的计算、TopK问题等的介绍

这篇关于C语言数据结构堆排序、向上调整和向下调整的时间复杂度的计算、TopK问题等的介绍的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---