代码随想录算法训练营第20天 |● 654.最大二叉树 ● 617.合并二叉树 ● 700.二叉搜索树中的搜索 ● 98.验证二叉搜索树

本文主要是介绍代码随想录算法训练营第20天 |● 654.最大二叉树 ● 617.合并二叉树 ● 700.二叉搜索树中的搜索 ● 98.验证二叉搜索树，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

---

前言

617，98只掌握了递归法

654.最大二叉树

思路

❤注意事项【本题简单，就这两个重要些儿】

1. 使用前序遍历
2. 可以在传入的时候传入数组和左右index而不是每次都复值一个数组的方式来节省空间开销。

老师在讲的思路和我下面有一点出入：
4. 他进入递归里面的nums不为空，长度大于等于1【题目给出的】，所以在切割左右数组的时候会加了限定index>0或者index<size-1，保证nums里面有元素才递归，我的方法会有空的情况【反正没错】。

方法一 递归法

下面是自己写的代码，一遍过，和昨天的一样思路，还比昨天的简单

class Solution(object):def constructMaximumBinaryTree(self, nums):""":type nums: List[int]:rtype: TreeNode"""if not nums: return Nonemax_val = max(nums) max_index = nums.index(max_val)node = TreeNode(val=max_val)#返回条件 叶子节点；本题中因为有了上面的None的情况，所以可以省略下面这一句判断if len(nums) == 1: return node# 单层递归逻辑#拆分左右left_tree = nums[:max_index]right_tree = nums[max_index+1:]node.left = self.constructMaximumBinaryTree(left_tree)node.right = self.constructMaximumBinaryTree(right_tree)return node

方法一2 老师的+优化递归法

思路：三步走

1. 返回node
2. 
3. 有3步
   
   
   

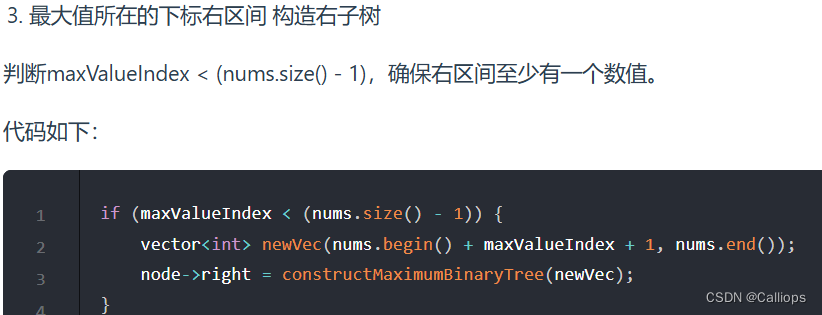
优化：没有必要每次传入的时候都是复值的一个新的小数组，只需要传入index的起止就可以了；

class Solution:def traversal(self, nums: List[int], left: int, right: int) -> TreeNode:if left >= right:return NonemaxValueIndex = leftfor i in range(left + 1, right):#不适用max和.index函数的写法。if nums[i] > nums[maxValueIndex]:maxValueIndex = iroot = TreeNode(nums[maxValueIndex])root.left = self.traversal(nums, left, maxValueIndex)root.right = self.traversal(nums, maxValueIndex + 1, right)return rootdef constructMaximumBinaryTree(self, nums: List[int]) -> TreeNode:return self.traversal(nums, 0, len(nums))

617.合并二叉树

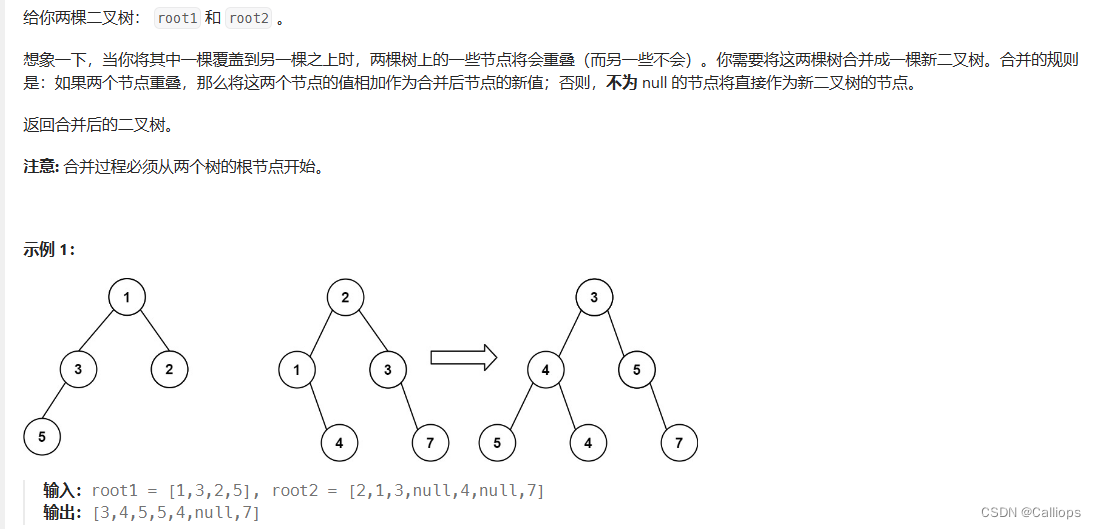
💌这是十分经典的二叉树题目；可以想想之前做过的对称二叉树；

思路

优先掌握递归法
总体思路：两棵树同步遍历+不是创建了一个新的二叉树，而是直接改的tree1；
三步递归法：

1. 输入和返回值：输入两个tree，输出root
2. 终止条件【💖十分巧妙】：如果t1为空，那么返回t2；如果t2为空，那就接t1
   • t1空了，肯定就是直接把后面的t2嫁接过来；当然t2为空也没有关系，那就接t2
3. 单层逻辑：val为t1的val+t2的val；左节点为t1.left和t2.left递归之后的结果，右边也是。
4. 补充：三种遍历顺序都是一样的

方法一 递归法

直接在t1上面处理，节省空间

class Solution(object):def mergeTrees(self, root1, root2):""":type root1: TreeNode:type root2: TreeNode:rtype: TreeNode"""if not root1:return root2if not root2:return root1root1.val += root2.valroot1.left = self.mergeTrees(root1.left,root2.left)root1.right = self.mergeTrees(root1.right,root2.right)return root1

方法二 迭代法

700.二叉搜索树中的搜索

思路

本题需要掌握递归法和迭代法，因为都很简单

方法一 递归法

三步走

1. 传入root，传出一个是搜索数值对应的节点
2. 终止条件：如果传入的为空的话，返回none；如果发现值相等target的话，也是直接返回root
3. 单层递归条件：如果整个值小于root的值，进入左子树递归；大的话就是右子树
4. 💘十分巧妙的点：终止条件里面两个可以合并，如果root==none，也是直接返回

class Solution(object):def searchBST(self, root, val):""":type root: TreeNode:type val: int:rtype: TreeNode"""if not root or root.val == val: return rootif root.val < val: result = self.searchBST(root.right)if root.val > val: result = self.searchBST(root.left)return result

方法二 迭代法

因为二叉搜索树的特性，所以很简单

class Solution:def searchBST(self, root: TreeNode, val: int) -> TreeNode:while root:if val < root.val: root = root.leftelif val > root.val: root = root.rightelse: return rootreturn None

98.验证二叉搜索树

注意：二叉搜索树是不可以有重复的

思路

总体思路：使用中序遍历（前中后），那么遍历过程中的元素应该是单调递增的。

方法一 使用数组

方法一：定义一个全局变量list，遍历一次append一次，如果是递增数组就是对的

class Solution(object):def __init__(self):self.vec = []def traversal(self,root):if not root: return Trueself.traversal(root.left)self.vec.append(root.val)self.traversal(root.right)def isValidBST(self, root):""":type root: TreeNode:rtype: bool"""if not root: return Trueself.traversal(root)for i in range(1,len(self.vec)):if self.vec[i-1] >= self.vec[i]:return Falsereturn True

方法二 不使用数组

方法二：不额外申请数组占据空间的方法，遍历的过程中直接比较。
陷阱：
陷阱1： 不能单纯的比较左节点小于中间节点，右节点大于中间节点就完事了；会出现下面的反面情况

陷阱2：

递归三部曲

1. 定义全局变量记录遍历过程中的最大值，输入为root输出为bool
2. 终止条件：如果为空节点，也是满足的。
3. 单层遍历的逻辑：前序递归；一直更新maxVal，一旦发现maxVal >= root->val，就返回false，注意元素相同时候也要返回false；后续递归–>最后返回的应该是前序和后序遍历的结果；

代码注意点：

1. python里面设定极小值的代码为 self.maxVal = float(‘-inf’)
2. 可以写>=的，，，，
3. 单层中结合左右中的结果来返回。别忘了返回左右的判断结果

class Solution:def __init__(self):self.maxVal = float('-inf')  # 因为后台测试数据中有int最小值def isValidBST(self, root):if root is None:return Trueleft = self.isValidBST(root.left)# 中序遍历，验证遍历的元素是不是从小到大if self.maxVal < root.val:self.maxVal = root.valelse:return Falseright = self.isValidBST(root.right)return left and right

方法二 使用双指针优化

为了解决方法二中的担忧：如果输入的就是int的最小值怎么办，如何给maxvalue初始化呢？使用双指针法来优化
定义一个全局指针pre，单层的逻辑修改为if (pre != NULL && pre->val >= root->val) return false;pre = root; // 记录前一个节点

class Solution(object):def __init__(self):self.pre = None def isValidBST(self, root):""":type root: TreeNode:rtype: bool"""if not root: return Trueleft = self.isValidBST(root.left)if self.pre and self.pre.val >= root.val: return Falseself.pre = rootright =  self.isValidBST(root.right)return left  and right

方法三 递归法

---

总结

today还是太慢了。一直在玩，实验都没有怎么做。

这篇关于代码随想录算法训练营第20天 |● 654.最大二叉树 ● 617.合并二叉树 ● 700.二叉搜索树中的搜索 ● 98.验证二叉搜索树的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---