本文主要是介绍视觉SLAM十四讲:从理论到实践(Chapter6:非线性优化),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
前言
学习笔记,仅供学习,不做商用,如有侵权,联系我删除即可
一、目标
- 理解最小二乘法的含义和处理方式。
- 理解高斯牛 顿法(Gauss-Newton's method)、列文伯格一马夸尔特方法(Levenburg-Marquadt's method)等下降策略。
- 学习Ceres库和g2o库的基本使用方法。
二、状态估计问题
2.1 批量状态估计和最大后验估计
经典的SLAM系统的观测方程:
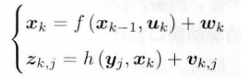
视觉SLAM系统的观测方程:
![]()
早期是用滤波的方法进行状态最优估计,现在主流的方法是非线性优化的方法。
与SLAM的损失函数一致的是运动结构重建,但运动结构重建(SfM,Structure from Motion)不是实时的,且是无时间顺序图像,不符合SLAM的需求。


由于条件概率分布很难求,所以对于工程应用方面,转换成求最大值的问题:最大后验估计(MAP),由于视觉SLAM没有先验,所以最后转化为最大似然估计(Maximize Likelihood Estimation, MLE):
![]()
最大似然估计——可以理解为——在位姿x,标志点y状态下,最可能产生现在观测到的数据。
2.2 最小二乘法引出

数学方面的推导过程:

对于视觉SLAM系统,结合数学形式的推导,(6.9)式的第一项与位姿无关,所以最大似然变为求第二项的负对数最小化:

最终的目标函数形式转化为:
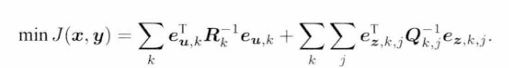
三、非线性最小二乘
通用迭代流程:

3.1 一阶和二阶梯度法
将目标函数在xk附近泰勒展开:
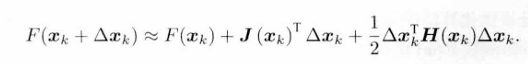
J:Fx对x的一阶导数,也叫梯度、Jacobian矩阵

H:二阶导数,Hessian矩阵

最速下降法:只保留一次项,为了保证函数下降,只需要:![]()
Newton法:保留二次项 , ![]()
3.2 高斯牛顿法
先平方,后展开——最速下降法(存在不稳定的问题)、Newton法(需要求二阶梯度Hessian矩阵)
先展开,后平方——GN算法(用一阶梯度代替二阶梯度),LM算法(在GN的基础上增加了一个范围条件)
对函数fx本身进行一阶展开,不是对目标函数Fx进行一阶展开:
![]()
在这种情况下,再将目标函数展开:
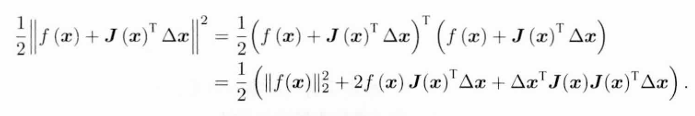

所以有正规方程:![]()
GN步骤:

但是GN法不能保证H是可逆的
3.3 列文伯格-马夸尔特方法(LM法)
依旧是这个近似模型:
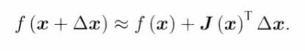
近似程度的描述:

ρ的分子是实际函数下降的值,分母是近似模型下降的值。ρ越小,表明近似模型过大,要减小Δx,反之同理。
步骤:

即相当于求解:![]()
总结
非线性优化是个很大的主题,研究者们为之奋斗多年;
主要方法:最速下降、牛顿、G-N、L-M、DogLeg等;
与线性规划不同,非线性需要针对具体问题具体分析;
问题非凸时,对初值敏感,会陷入局部最优,目前没有非凸问题的通用最优值的寻找办法;
问题凸时,二阶方法通常一两步就能收敛。
这篇关于视觉SLAM十四讲:从理论到实践(Chapter6:非线性优化)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




