本文主要是介绍数据结构算法-堆(Heap)和优先队列,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
堆的概念
堆(heap)是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵树的数组对象。堆总是满足下列性质:
- always greater than its child node/s and the key of the root node is the largest among all other nodes. This property is also called max heap property.
- always smaller than the child node/s and the key of the root node is the smallest among all other nodes. This property is also called min heap property.
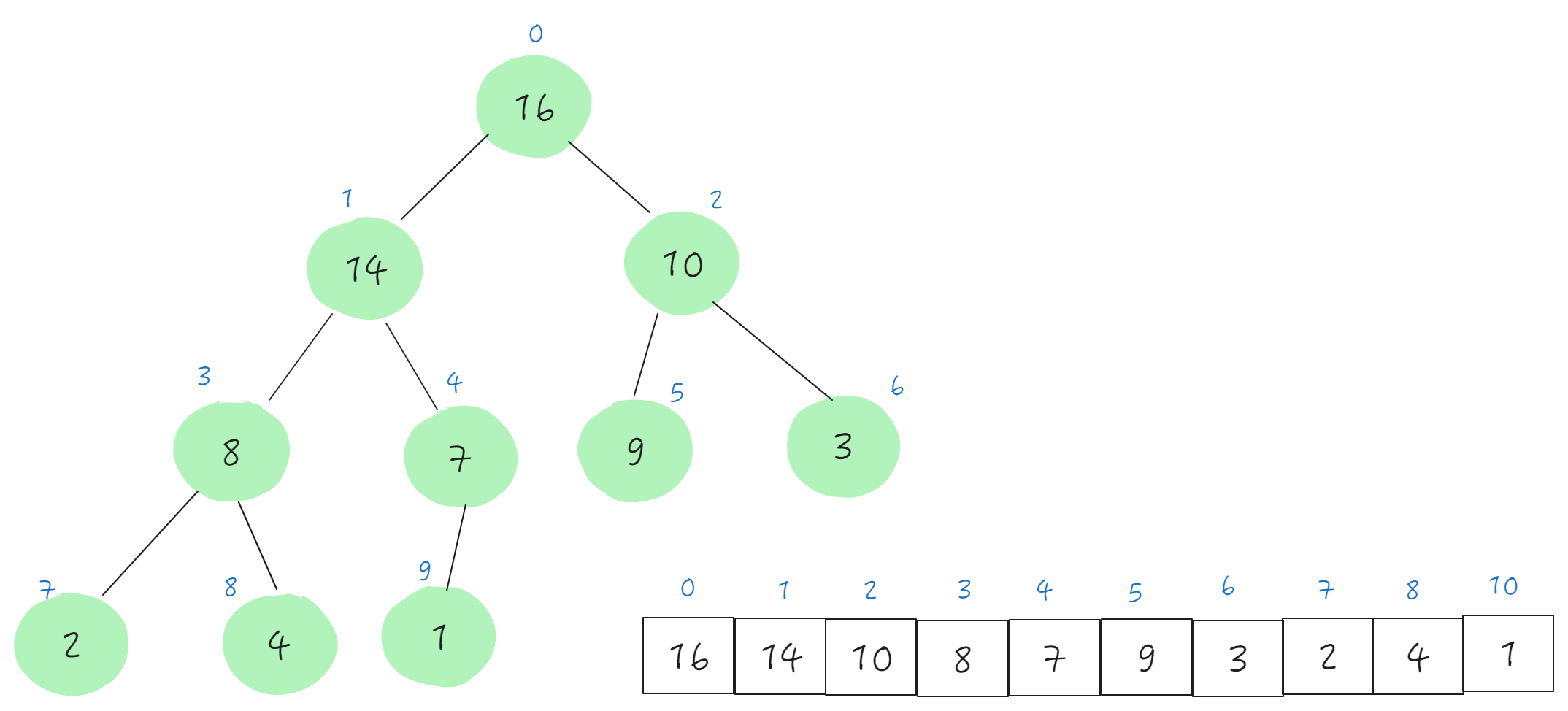
最大堆
最大堆是指在树中,存在一个结点而且该结点有儿子结点,该结点的data域值都不小于其儿子结点的data域值。
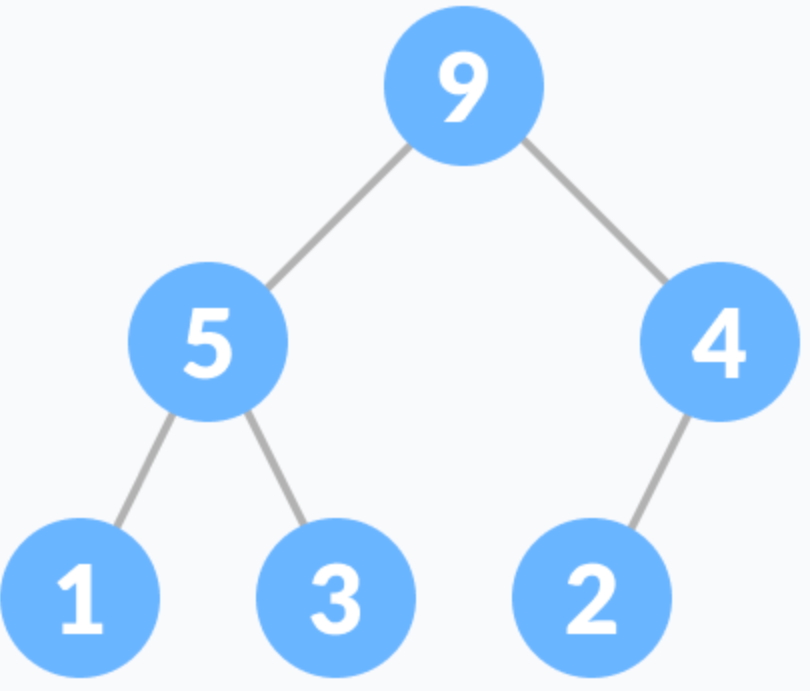
最小堆
最小堆是指在树中,存在一个结点而且该结点有儿子结点,该结点的data域值都不大于其儿子结点的data域值。
堆的操作
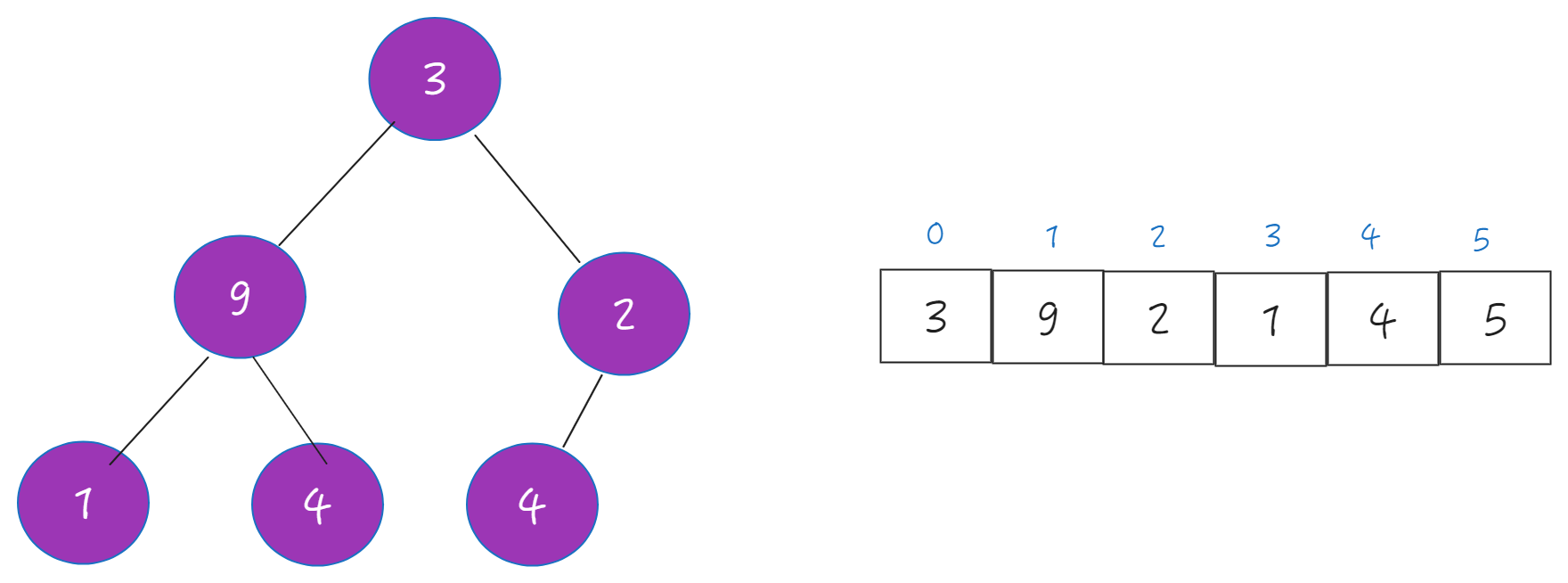
Heapify
Heapify is the process of creating a heap data structure from a binary tree. It is used to create a Min-Heap or a Max-Heap.
heapify是将heap调整为最大堆或最小堆的过程,我们以最大堆为例,演示调整过程。
找到最后一个非叶子节点
heapify是从当前最后一个非叶子结点开始,一直向下到0.
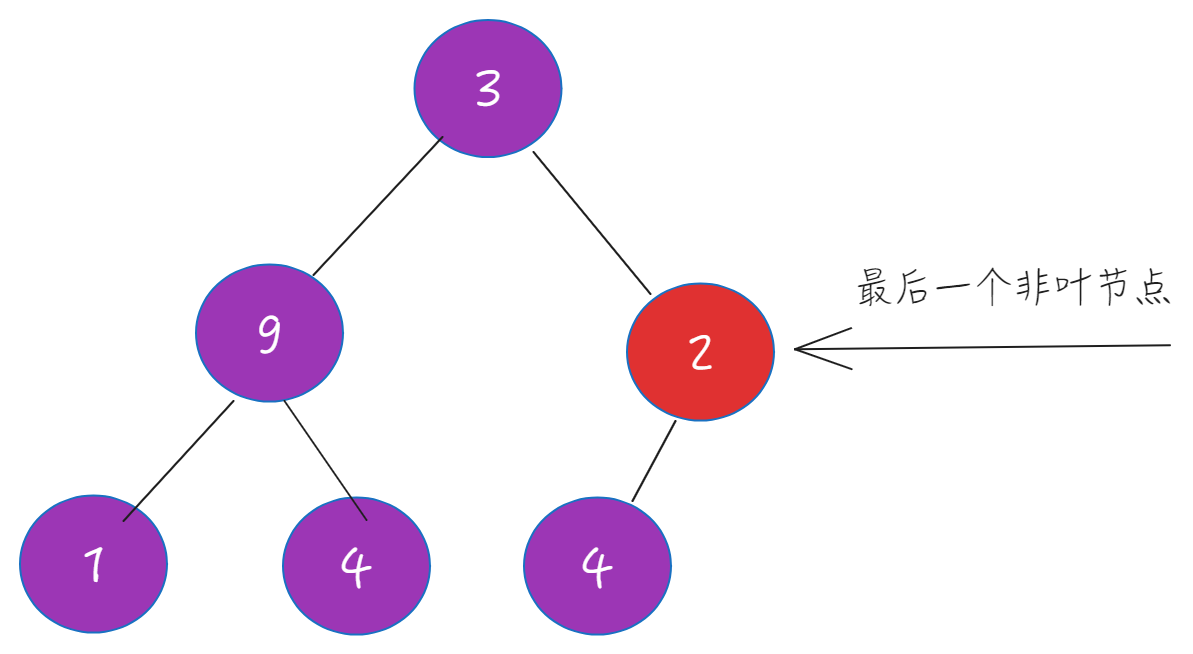
如何找到最后一个非叶子节点
一个数组(假设长度为n)构成的完全二叉树,index表示节点索引索引,
个人理解: 叶节点的数量大致为其父节点的2倍(子节点最多两个子节点,假设为满完全二叉树),最后一个节点约等于叶节点的第一个节点(约为n/2)-1: 大致为n/2-1
叶节点和(假设四层) 约等于 (1,2,3)层之和
| 编号 | 层(k) | 索引(index) | 层和索引 | n和索引 |
|---|---|---|---|---|
| 1 | 1 | 0 | 2k-1-1 | |
| 2 | 2 | 1,2 | 2k-1-1, 2k-1 | 节点2:(6/2)-1 =2 |
| 3 | 3 | 3,4,5,6 | 2k-1-1 | 节点6(假设有): 15/2-1=6 |
| 4 | 4 | 7,8,9,10,11,12,13,14 |
设置当前的为最大元素
int largest = i;
int len = size; // 数组实际长度
//3. 计算当前节点的左子节点,和右子节点
int left = 2 * i + 1; //左子节点位置
int right = 2 * i + 2; //右子节点位置
right = Math.min(right,elements.length-1);
当前节点与左子和右子比较,找到最大值
// 3.1比较左子节点
if (left<size && elements[left] > elements[largest]) {largest = left;
}
if (right<size && elements[right] > elements[largest]) {largest = right;
}
与当前节点交换最大值
//交换largset
int tmp = elements[largest];
elements[largest] = elements[i];
elements[i] = tmp;
//用户当前节点递归heapify
heapify(largest);
从最后一个非叶子结点开始
从最后一个非叶节点依次递减到0,循环执行以上步骤
for(int i = elements.length/2-1; i>=0;i++){heapify(i);
}
heapify完整代码
public void heapify(int curr) {//1.找到最后一个非叶节点int len = elements.length;System.out.println("curr: " + curr);//2. 设置当前节点为最大节点int largest = curr;//3. 计算当前节点的左子节点,和右子节点int left = 2 * curr + 1;int right = 2 * curr + 2;// 3.1比较左子节点if (left < size && elements[left] > elements[largest]) {largest = left;}if (right < size && elements[right] > elements[largest]) {largest = right;}//交换largsetif (largest != curr) {int tmp = elements[largest];elements[largest] = elements[curr];elements[curr] = tmp;// 递归地heapify受影响的子树(以新的最大值节点为根) // 这会确保子树也保持最大堆的性质 heapify(largest);}
}
在堆中添加数据
public void insert(int data) {if (size == 0) {elements[size++] = data;} else {elements[size++] = data;for (int i = size / 2 - 1; i >= 0; i--) {heapify(i);}}
}
添加第一个数: 1
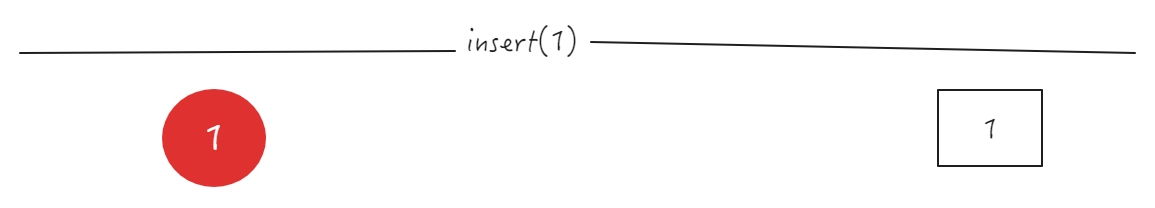
添加第二个数: 9
第二个数9作为1的左子节点进行比较大于1,交换两个值,largest=1
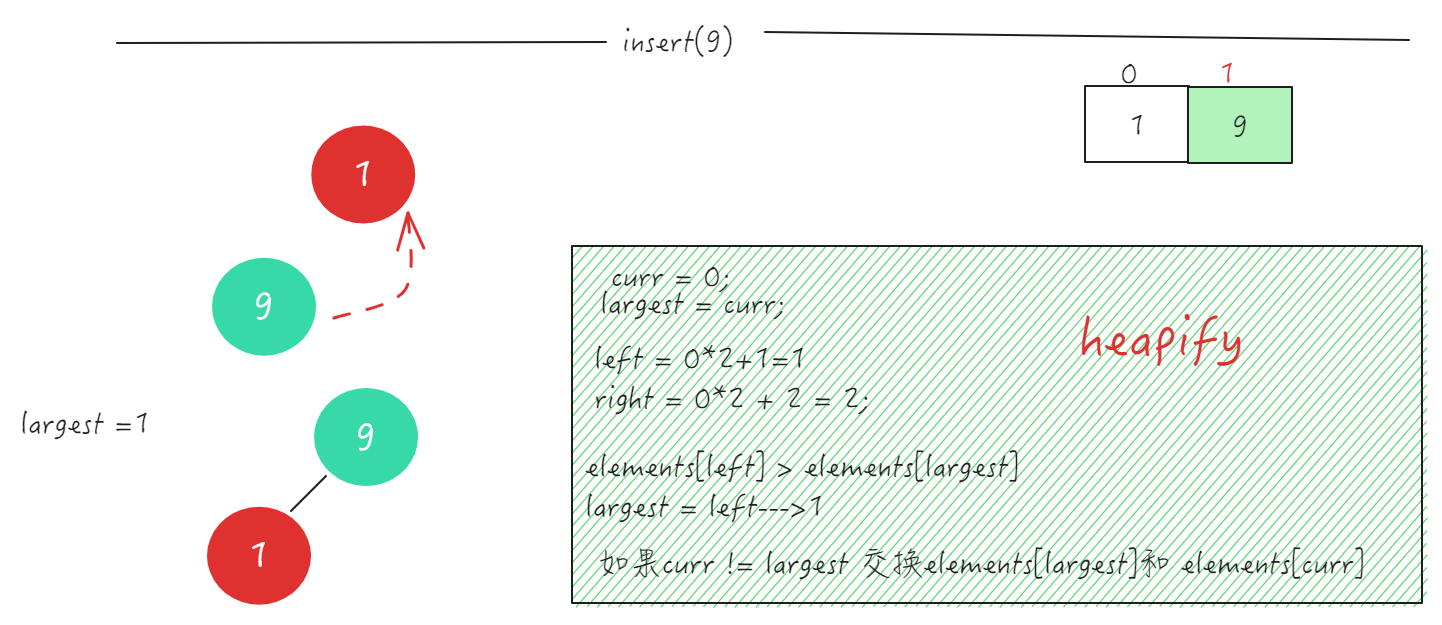
添加第三个数: 5
5作为第三个数,与它的父节点9比较,小于父节点,所以不做交换。

添加第四个数: 4
第四个节点按照完全二叉树的定义从左向右添加,作为节点(值=1)的子节点。需要heapify(), 节点(值=4)与节点(值=1)进行交换。

删除堆中的元素
选取要删除的元素
int wantedDelIndex;
for(wantedDelIndex =0; wantedDelIndex < size;wantedDelIndex++){if(data == elements[wantedDelIndex]) break;
}
将当前元素与最后一个元素交换
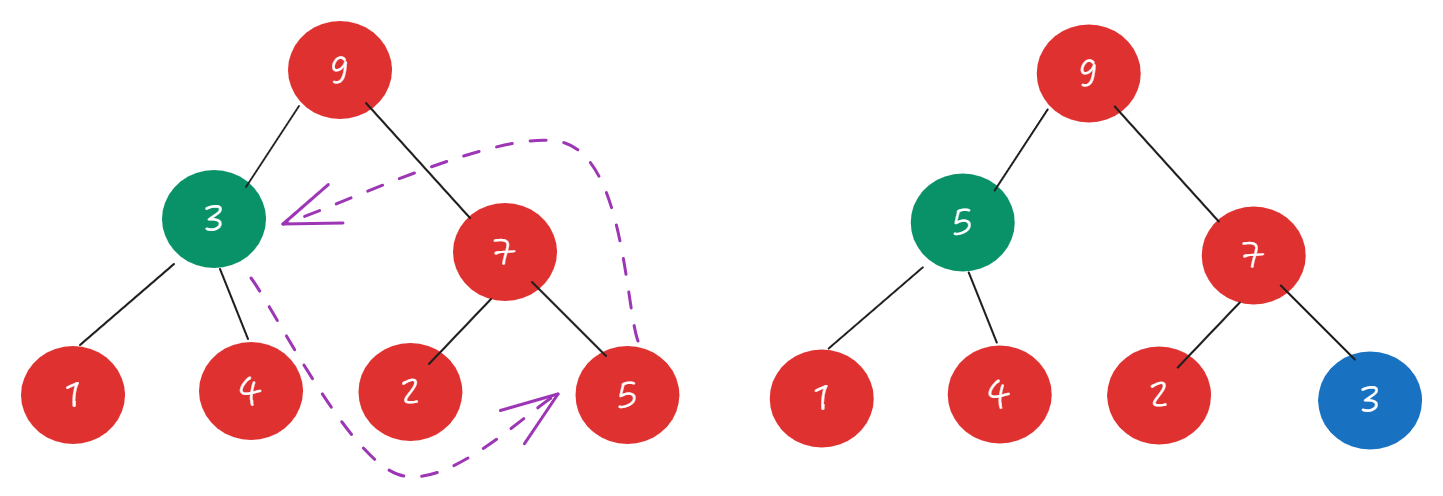
/*将要删除的元素与最后一个叶节点元素交换*/
int tmp = elements[wantedDelIndex];
elements[wantedDelIndex] = elements[size-1];
elements[size-1] = tmp;
删除最后一个叶节点
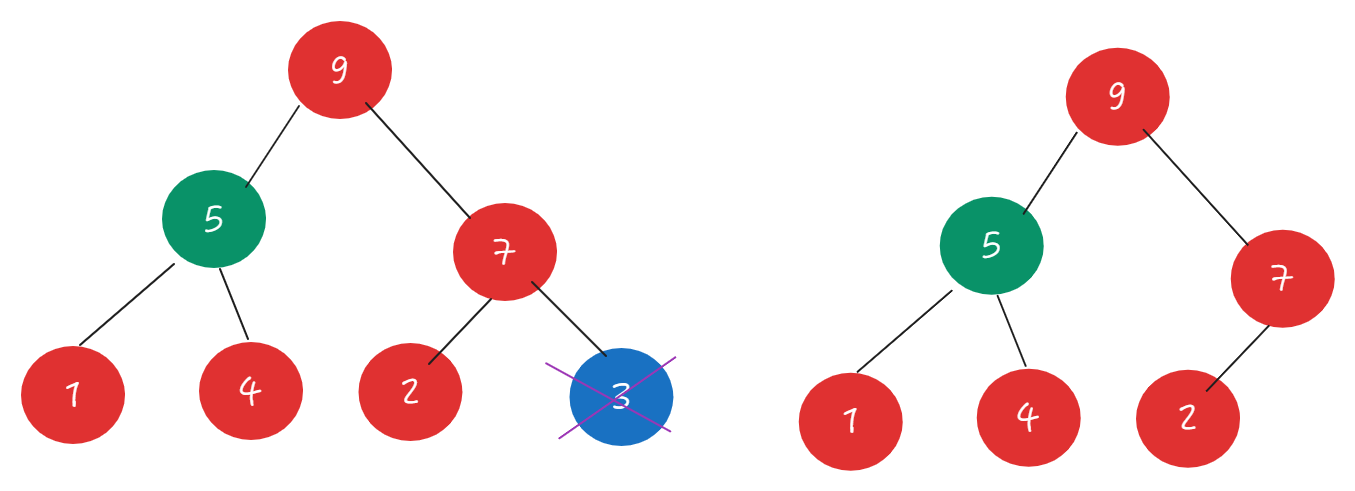
heapify
调用heapify()方法
力扣“前K个高频元素”
https://leetcode.cn/problems/top-k-frequent-elements/description/
给你一个整数数组 nums 和一个整数 k ,请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。
示例 1:
输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]
示例 2:
输入: nums = [1], k = 1
输出: [1]
使用Map存储每个元素的值和出现频率,再将Map中的Map.entry对象放入,注意: Map.entry对象已经实现了Comparator方法,即可以存入优先队列(优先队列的底层由最小堆完成). 以下给出自己的参考实现。
class Solution {public int[] topKFrequent(int[] nums, int k) {Map<Integer, Integer> map = new HashMap<>();PriorityQueue<Map.Entry<Integer, Integer>> queue = new PriorityQueue<>(Map.Entry.comparingByValue());for (int t : nums) {map.merge(t, 1, Integer::sum);}queue.addAll(map.entrySet());int n = map.size();int[] a = new int[k];for (int i = 0; i < n - k; i++) {queue.poll();}for (int i = 0; i < k; i++) {a[i] = Objects.requireNonNull(queue.poll()).getKey();}return a;}
}
这篇关于数据结构算法-堆(Heap)和优先队列的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








