本文主要是介绍C语言PTA练习题(编程求1+3+5+...+n,编程求n的阶乘,爬楼梯,爬楼梯(扩展),猴子吃桃,猴子吃桃(扩展),求算式前n项的和,汉诺塔游戏),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
7-1 编程求1+3+5+...+n
输入一个正整数n,编程求1+3+5+...+n
要求:用递归完成。
输入格式:
输入一行,只有一个整数n (1<=n<=9999) 这里n为奇数。
输出格式:
一个正整数,表示结果。
输入样例:
在这里给出一组输入。例如:
9
输出样例:
在这里给出相应的输出。例如:
25
#include<stdio.h>
int digui(int n) {if (n == 1) {return 1;}else {return digui(n - 2) + n;}
}
int main() {int n;scanf("%d", &n);printf("%d\n", digui(n));return 0;
}
7-2 编程求n的阶乘
输入一个正整数n,编程求n的阶乘n!。n!=1*2*3*...*n
要求:用递归完成。
输入格式:
输入一行,只有一个整数n (1<=n<=20)。
输出格式:
一行,结果。
输入样例:
在这里给出一组输入。例如:
4
输出样例:
在这里给出相应的输出。例如:
24
#include<stdio.h>
long digui(int n) {if (n == 1) {return 1;}else {return digui(n-1)*n;}
}
int main() {int n;scanf("%d", &n);if(n==0){printf("1");}else{printf("%ld\n", digui(n));}return 0;
}
7-3 爬楼梯
小明爬楼梯,他可以每步可以走1级或者2级,输入楼梯的级数n,求不同的走法数。
例如:n=3,表示楼梯一共有3级,他可以每次都走一级,或者第一次走一级,第二次走两级,也可以第一次走两级,第二次走一级,一共3种方法。
要求:用递归完成。
输入格式:
输入一个正整数n,代表楼梯级数,1≤n≤30。
输出格式:
一个正整数,表示一共有多少种不同的走法。
输入样例:
在这里给出一组输入。例如:
5
输出样例:
在这里给出相应的输出。例如:
8#include<stdio.h>
int digui(int n) {if (n == 1) {return 1;}else if (n == 2) {return 2;}else {return digui(n-1)+digui(n-2);}
}
int main() {int n;scanf("%d", &n);printf("%d\n", digui(n));return 0;
}
7-4 爬楼梯(扩展)
小明爬楼梯,他可以每步可以走1级、2级、3级,输入楼梯的级数n,求不同的走法数。
例如:n=3,表示楼梯一共有3级,他可以每次都走一级;或者第一次走一级,第二次走两级;也可以第一次走两级,第二次走一级;还可以一步走3级;一共4种方法。
要求:用递归完成。
输入格式:
输入一个正整数n,代表楼梯级数,1≤n≤30。
输出格式:
一个正整数,表示一共有多少种不同的走法。
输入样例:
在这里给出一组输入。例如:
4
输出样例:
在这里给出相应的输出。例如:
7#include<stdio.h>
int digui(int n) {if (n == 1) {return 1;}else if (n == 2) {return 2;}else if (n == 3) {return 4;}else {return digui(n-1)+digui(n-2)+digui(n-3);}
}
int main() {int n;scanf("%d", &n);printf("%d\n", digui(n));return 0;
}
7-5 猴子吃桃
猴子吃桃子问题:猴子第一天摘下若干个桃子,当即吃了一半还不过瘾,又多吃了一个;第二天又将剩下的桃子吃掉一半又多吃了一个;以后每天早上都吃了前一天剩下的一半零一个。到了第n天想再吃时,见只剩下一个桃子,求第一天共摘了多少个桃子?
要求:用递归实现。
输入格式:
一个整数n(1≤n≤62),表示最后一天第 n 天看到还剩1个桃子。
输出格式:
一个整数,第一天共有多少个桃子
输入样例:
在这里给出一组输入。例如:
10
输出样例:
在这里给出相应的输出。例如:
1534
#include<stdio.h>
long digui(int n) {if (n == 1) {return 1;}else {return (digui(n-1)+1)*2;}
}
int main() {int n;scanf("%d", &n);printf("%ld\n", digui(n));return 0;
}
7-6 猴子吃桃(扩展)
猴子第一天摘了X个桃子,当即吃掉了一些桃子,剩下X的平方根个桃子,还不过瘾,又多吃了一个,剩下Y个;第二天又吃掉了一些,剩下Y的平方根个桃子,又多吃一个;以后每天早上都吃到剩下当前的平方根个桃子,再多吃一个。到了第n天想再吃时,见只剩下一个桃子,求第一天共摘了多少个桃子?
要求:用递归完成。
输入格式:
一个整数n(1≤n≤6),表示最后一天第 n 天看到还剩1个桃子。
输出格式:
一个整数,第一天共有多少个桃子
输入样例:
在这里给出一组输入。例如:
3
输出样例:
在这里给出相应的输出。例如:
25#include<stdio.h>
long digui(int n) {if (n == 1) {return 1;}else {return (digui(n-1)+1)* (digui(n - 1) + 1);}
}
int main() {int n;scanf("%d", &n);printf("%ld\n", digui(n));return 0;
}
7-7 求算式前n项的和
求1+1/2+2/3+3/5+5/8+8/13+13/21……的前n项的和。
要求:用递归完成
输入格式:
第1行:一个整数n(1 <= n <= 30 )。
输出格式:
一行:一个小数,即前n项之和(保留3位小数)。
输入样例:
在这里给出一组输入。例如:
5
输出样例:
在这里给出相应的输出。例如:
3.392
#include<stdio.h>
int main()
{int i, n;double a = 1, b = 1, c, d, sum = 0;scanf("%d", &n);if (n >= 1 && n <= 30)for (i = 1; i <= n; i++){d = a / b;sum += d;c = a;a = b;b = c + a;}printf("%.3f\n", sum);return 0;
}7-8 汉诺塔游戏
汉诺塔(Hanoi Tower)问题是印度的一个古老的传说。开天辟地的神勃拉玛在一个庙里留下了三根金刚石的棒,第一根上面套着64个圆的金片,最大的一个在底下,其余一个比一个小,依次叠上去,庙里的众僧不倦地把它们一个个地从这根棒搬到另一根棒上,规定可利用中间的一根棒作为帮助,但每次只能搬一个,而且大的不能放在小的上面。面对庞大的数字(移动圆片的次数)18446744073709551615,看来,众僧们耗尽毕生精力也不可能完成金片的移动。
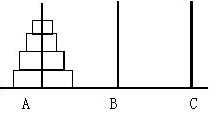
后来,这个传说就演变为汉诺塔游戏:
1.有三根杆子A,B,C。A杆上有若干碟子
2.每次移动一块碟子,小的只能叠在大的上面
3.把所有碟子从A杆全部移到C杆上
经过研究发现,汉诺塔的破解很简单,就是按照移动规则向一个方向移动金片:
如3阶汉诺塔的移动:A→C, A→B, C→B, A→C, B→A, B→C, A→C
输入格式:
一个整数N,表示A柱上有N个碟子(0<n<=10)。
输出格式:
若干行,即移动的最少步骤的每一步(从哪个柱到哪个柱)
最后一行输出最小的移动步数
输入样例:
在这里给出一组输入。例如:
3
输出样例:
在这里给出相应的输出。例如:
A To C
A To B
C To B
A To C
B To A
B To C
A To C
7#include <stdio.h>
void move(char sour, char dest) {printf("%c To %c\n", sour, dest);
}
void towerOfHanoi(int num, char sour, char aux, char dest) {if (num == 1) {move(sour, dest);return;}towerOfHanoi(num - 1, sour, dest, aux);move(sour, dest);towerOfHanoi(num - 1, aux, sour, dest);
}int main() {int num;scanf("%d", &num);towerOfHanoi(num, 'A', 'B', 'C');printf("%lld", (1LL << num) - 1);return 0;
}这篇关于C语言PTA练习题(编程求1+3+5+...+n,编程求n的阶乘,爬楼梯,爬楼梯(扩展),猴子吃桃,猴子吃桃(扩展),求算式前n项的和,汉诺塔游戏)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!


