本文主要是介绍【图论及其运用 — 电子科技大学】(三)第三章 图的连通性,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、图的连通性刻画
(⼀)、割边及其性质
定义1 边 e e e为图 G G G的⼀条割边,如果 ω ( G − e ) > ω ( G ) ω(G − e) > ω(G) ω(G−e)>ω(G)。( ω ( G ) ω(G) ω(G) 表示图 G G G 连通分支的数量, G − e G − e G−e 表示只去掉 e e e 这条边,边两边的点不动)


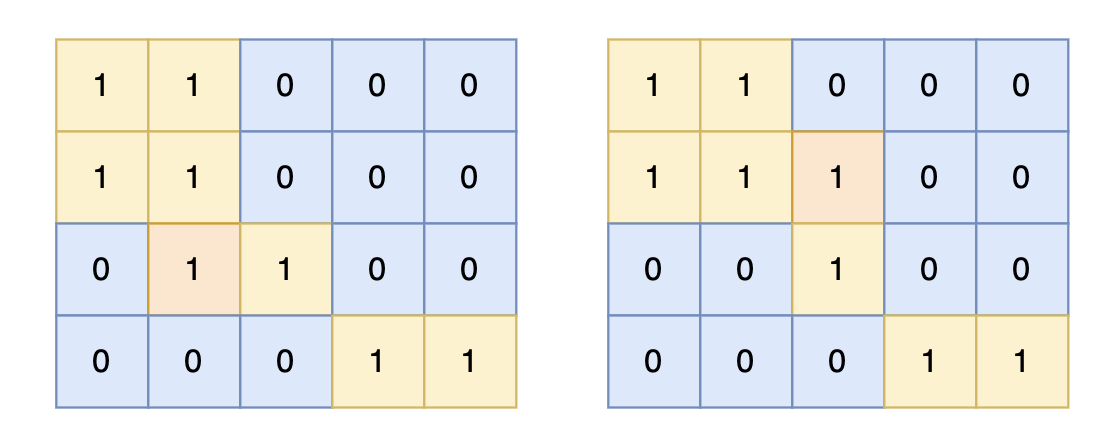
e 2 e_2 e2 为割边,是因为去掉 e 2 e_2 e2 这条边后只剩下右边一个点,与其他部分不连通
注: 割边⼜称为图的“桥”。
图的割边有如下性质:
定理1 边 e e e 是图 G G G的割边当且仅当 e e e 不在 G G G 的任何圈中。
证明: 可以假设 G G G 连通。
“必要性” ( e e e 是图 G G G的割边 一定有 e e e 不在 G G G 的任何圈中)
(反证法)若不然。设 e e e 在图 G G G 的某圈 C C C 中,且令 e = u v e = uv e=uv. 考虑 P = C − e P = C- e P=C−e, 则 P P P是⼀条 u v uv uv 路。下⾯证明 G − e G-e G−e 连通。 对任意 x , y ∈ V ( G − e ) x, y \in V(G-e) x,y∈V(G−e),由于 G G G 连通,所以存在 x → y x \to y x→y 路 Q Q Q. 若 Q Q Q 不含 e e e,则 x x x 与 y y y 在 G − e G-e G−e ⾥连通;若 Q Q Q 含有 e e e,则可选择路: x → u P v → y x \to u P v \to y x→uPv→y, 说明 x x x 与 y y y 在 G − e G-e G−e ⾥也连通。所以, 若边 e e e 在 G G G 的某圈中,则 G − e G-e G−e 连通。但这与e是G的割边⽭盾!
“充分性” ( e e e 不在 G G G 的任何圈中,则 e e e 是图 G G G的割边)
(反证法)若不然,如果 e e e不是 G G G的割边,则 G − e G-e G−e连通,于是在 G − e G-e G−e中存在⼀条 u → v u \to v u→v 路,显然:该路并上边 e e e得到 G G G中⼀个包含边 e e e的圈,与 e e e 不在 G G G 的任何圈中⽭盾。
推论1 e e e 为连通图 G G G 的⼀条边,如果 e e e 含于 G G G 的某圈中,则 G − e G-e G−e 连通。
证明: 若不然, G − e G-e G−e 不连通,于是 e e e 是割边。由定理 1, e e e 不在 G G G 的任意圈中,⽭盾!
k 正则二部图:设 ∣ X ∣ = n 1 , ∣ Y ∣ = n 2 |X|=n_1,|Y|=n_2 ∣X∣=n1,∣Y∣=n2,有 n 1 = n 2 n_1 = n_2 n1=n2
假设 n 1 ≠ n 2 n_1≠n_2 n1=n2,不妨设 n 1 > n 2 n_1>n_2 n1>n2,由于是 K K K正则的,故由 X X X点集引出的边有 n 1 × k n_1×k n1×k条,同时连向 Y Y Y 这个点集的边数亦为 n 1 × k n_1×k n1×k 条(亦即由 Y Y Y 点集引出的边数为 n 1 × k n_1×k n1×k)。
由于是正则的二分图,故 Y Y Y 点集的每个点的度数为 n 1 × k / n 2 n_1×k/n_2 n1×k/n2,而 n 1 / n 2 > 1 n_1/n_2>1 n1/n2>1,故 Y Y Y 中点的度数 > k k k,这与 G G G 是一个 k k k 正则图矛盾,从而必有 X , Y X,Y X,Y 的模相等。
k 正则二部图是一种特殊的二部图,它具有如下性质: 对于二部图的任意一个顶点,它与同一部分中的其他顶点的度数都相等,并且这个度数等于另一部分中所有顶点的度数之和的 1 / k 1/k 1/k。这里的 k k k 是一个正整数,表示图的正则度。

注意偶图中, X X X 中的度之和 = Y Y Y 中的度之和,因为每条边,一条边在 X X X 中,一条边在 Y Y Y 中
(⼆)、割点及其性质
定义2 在 G G G中,如果 E ( G ) E(G) E(G)可以划分为 两个⾮空⼦集 E 1 E1 E1 与 E 2 E2 E2, 使 G [ E 1 ] G[E1] G[E1] 和 G [ E 2 ] G[E2] G[E2] 以点 v v v 为公共顶点,称 v v v 为 G G G 的⼀个割点。( E ( G ) E(G) E(G) 表示边集,注意 E 1 E1 E1 与 E 2 E2 E2 非空,即两个集合存在边,而不是简单的只有点)

定理2 G G G⽆环且⾮平凡,则 v v v是 G G G的割点,当且仅当 ω ( G − v ) > ω ( G ) ω(G − v) >ω(G) ω(G−v)>ω(G)
证明:
“必要性”
设 v v v是 G G G的割点。则 E ( G ) E(G) E(G)可划分为两个⾮空边⼦集 E 1 E1 E1与 E 2 E2 E2, 使 G [ E 1 ] , G [ E 2 ] G[E1],G[E2] G[E1],G[E2] 恰好以 v v v 为公共点。
由于 G G G 没有环,所以, G [ E 1 ] , G [ E 2 ] G[E1],G[E2] G[E1],G[E2] 分别⾄少包含异于 v v v的 G G G 的点,这样, G − v G-v G−v 的分⽀数⽐ G G G的分⽀数⾄少多 1 1 1,所以: ω ( G − v ) > ω ( G ) ω(G − v) >ω(G) ω(G−v)>ω(G)
“充分性”
由割点定义结论显然。
× × × \color{red}××× ××× 定理3 v v v 是树 T T T 的顶点,则 v v v 是割点,当且仅当 v v v 是树的分⽀点。(内点和树根统称为分支点,而树根不能作为割点)

定理3 v v v 是树 T T T 的顶点,则 v v v 是割点,当且仅当 d ( v ) > 1 d(v) > 1 d(v)>1。

定理4 设 v v v是⽆环连通图 G G G的⼀个顶点,则 v v v是 G G G的割点,当且仅当 V ( G − v ) V(G-v) V(G−v)可以划分为两个⾮空⼦集 V 1 V_1 V1与 V 2 V_2 V2, 使得对任意 x ∈ V 1 , y ∈ V 2 x ∈V_1, y ∈V_2 x∈V1,y∈V2, 点 v v v在 x y x y xy路上。


恰有两个非割点,所以由 n - 2 个割点
单图即简单图


(三)、块及其性质
定义3 没有割点的连通图称为是⼀个块图,简称块; G G G 的⼀个⼦图 B B B称为是 G G G的⼀个块,如果(1)它本身是块;(2)若没有真包含 B B B的 G G G的块存在。(即子块 B B B 不能再产生子块 B B B 的子块)

图 G G G 是块满足如下:
- 当阶数大于等于 3,且无环(有环一定可以产生一个割点),则块一定有圈(即任意两点一定在同一圈上)
- 当阶数等于 2,且无环,则是割边
- 当阶数为 1,则是环,或孤立点
由定义3 可推知: 若 e e e 是图 G G G 的割边或 e e e 是一个环,则 G [ { e } ] G[\{e\}] G[{e}] 是 G G G 的块; G G G 的仅含一个点的块或是孤立点,或是环导出的子图;至少两个点的块无环,至少三个点的块无割边。
对于任意图 G G G,由于块是联通的,所以若 B B B 是图 G G G 的块,则 B B B 也是 B B B 所在联通分支的块。反之若 B B B 是 G G G 的某联通分支的块,则 B B B 也是 G G G 的块
定理5 若 ∣ V ( G ) ∣ ≥ 3 |V(G)| ≥ 3 ∣V(G)∣≥3, 则 G G G 是块,当且仅当 G G G⽆环且任意两顶点位于同⼀圈上。

定理6 点 v v v是图 G G G的割点当且仅当 v v v⾄少属于 G G G的两个不同的块。

最后一句 B 1 ∪ B 2 ∪ P B_1 \cup B _2 \cup P B1∪B2∪P 整体无割点,即说明了,这个整体不能划分为两个块,整体只是一个块
注: 该定理揭示了图中的块与图中割点的内在联系:不同块的公共点一定是图的割点。也就是说,图的块可以按割点进行寻找。所以,该定理的意义在于:可以得到寻找图中全部块的算法。
为了直观反映图的块和割点之间的联系,引进所谓的块割点树。
设 G G G是非平凡连通图。 B 1 , B 2 , . . . , B k \mathrm{B_1,B_2,...,B_k} B1,B2,...,Bk 是 G G G 的全部块,而 v 1 , v 2 , . . . , v t \mathbf{v_1,v_2,...,v_t} v1,v2,...,vt 是 G G G 的全部割点。构作 G G G 的块割点树 b c ( G ) bc(G) bc(G):它的顶点是 G G G的块和割点,连线只在块割点之间进行,一个块和一个割点连线,当且仅当该割点是该块的一个顶点。

P65—66 习题3 : 1, 2, 3,5,7,8
二、网络的容错性参数
(一)、连通度的概念与性质
1、点连通度与边连通度的概念
定义1 给定连通图 G G G,设 V ′ ⊆ V ( G ) V^{\prime}\subseteq V(G) V′⊆V(G),若 G − V ′ G -V^{'} G−V′ 不连通,称 V ′ V^{'} V′ 为 G G G 的一个点割集,含有 k k k 个顶点的点割集称为 k k k 顶点割。 G G G 中点数最少的顶点割称为最小顶点割。

定义2 在 G G G中,若存在顶点割,称 G G G的最小顶点割的顶点数称为 G G G的点连通度;否则称 n − 1 n-1 n−1为其点连通度。 G G G的点连通度记为 κ ( G ) \kappa(G) κ(G), 简记为 κ \kappa κ。若 G G G不连通, κ ( G ) = 0 \kappa(G)=0 κ(G)=0。
连通度也可描述为 “删去图中 k k k( k k k 可为 0 0 0) 个点,使图不连通或成为平凡图的最小 k k k 值”

G 2 G_2 G2 不存在顶点割,所以 κ ( G ) = n − 1 = 3 \kappa(G)=n - 1 = 3 κ(G)=n−1=3
- 非平凡树的连通度均为 1
- 完全图没有顶点割,以完全图为生成子图的图也没有顶点割(实际上完全图的顶点割为删除完全图中的所有顶点,只留一个,实现不连通)
- 单个割点可以作为 1 顶点割
- 当且仅当 κ ≥ 1 \kappa ≥ 1 κ≥1,图连通
定义3 (1)设 G G G 为连通图,称使 G − E ′ G - E{'} G−E′ 不连通的 G G G 的边子集 E ′ E{'} E′ 为 G G G 的边割,含有 k k k 条边的边割为 k k k 边割。边数最少的边割称为最小边割
(2) 设 G G G 是非平凡连通图,若 M M M 是 G G G 的最小边割集,则称 ∣ M ∣ |M| ∣M∣ 为 G G G 的边连通度。边连通度记为 λ ( G ) λ(G) λ(G) ,简记为 λ λ λ。若 G G G 不连通或 G G G 是平凡图,则定义 λ ( G ) = 0 λ(G) =0 λ(G)=0。
G 1 G_1 G1 中去掉 v 6 v_6 v6 连接的边,使得 v 6 v_6 v6 与其他点不联通
G 2 G_2 G2 中删去 v 1 v_1 v1 中与 v 1 v_1 v1 连接的三条边
G 3 G_3 G3 不连通,为 0

定义4 在 G G G中,若 κ ( G ) ≧ k \kappa(G)≧ k κ(G)≧k, 称 G G G是 k k k连通的或k连通图;若 λ ( G ) ≧ k λ(G)≧k λ(G)≧k,称 G G G是 k k k边连通的或 k 边连通图。

- 因此所有非平凡连通图均是 1 连通的、1 边连通的。
2、连通度的性质
定理1 (惠特尼1932) 对任意图 G G G,有:
κ ( G ) ≤ λ ( G ) ≤ δ ( G ) \kappa(G)\leq\lambda(G)\leq\delta(G) κ(G)≤λ(G)≤δ(G)
从两个方面去思考:(1) λ ( G ) ≤ δ ( G ) \lambda(G)\leq\delta(G) λ(G)≤δ(G):去掉顶点 u u u 与之关联的所有边,那顶点 u u u 一定与其他点不连通;(2) κ ( G ) ≤ λ ( G ) \kappa(G)\leq\lambda(G) κ(G)≤λ(G),去掉一条边,则可以去掉与之相关联的其中一个顶点。

定理2 设 G G G是 ( n , m ) (n, m) (n,m)连通图,则:
κ ( G ) ≤ ⌊ 2 m n ⌋ \kappa(G)\leq\left\lfloor\frac{2m}n\right\rfloor κ(G)≤⌊n2m⌋

哈拉里通过构图的方式证明了定理2的界是紧的。即存在一个 ( n , m ) (n, m) (n,m) 图 G G G,使得:
κ ( G ) = ⌊ 2 m n ⌋ \kappa(G) = \left\lfloor\frac{2m}n\right\rfloor κ(G)=⌊n2m⌋
哈拉里图: 涉及可靠性通信网络构建
1962年,数学家哈拉里构造了连通度是 k k k,边数为 m = ⌊ n k 2 ⌋ m=\left\lfloor\frac{nk}2\right\rfloor m=⌊2nk⌋ 的图 H k , n H_{k, n} Hk,n ,称为哈拉里图。
(1) H 2 r , n H_{2r,n} H2r,n
V ( H ) = { 0 , 1 , 2 , ⋯ , n − 1 } V(H)=\begin{Bmatrix}0,1,2,\cdots,n-1\end{Bmatrix} V(H)={0,1,2,⋯,n−1}
E ( H ) = { i j ∣ ∣ i − j ∣ ≤ r ( 取模 n 的加法 ) } \left.E(H\right.)=\left\{ij\left|\left|i\right.-j\right|\leq r\left(\text{取模 }n\text{的加法}\right)\right\} E(H)={ij∣∣i−j∣≤r(取模 n的加法)}

(2) H 2 r + 1 , n H_{2r+1,n} H2r+1,n (n为偶数)
先作 H 2 r , n H_{2r,n} H2r,n, 然后对 1 ≦ i ≦ n / 2 , i 1≦i≦n/2,i 1≦i≦n/2,i 与 i + n / 2 i+n/2 i+n/2 连线。

(3) H 2 r + 1 , n H_{2r+1,n} H2r+1,n (n为奇数)
先作 H 2 r , n H_{2r,n} H2r,n, 然后对 1 ≦ i ≦ ( n − 1 ) / 2 , i 1≦i≦(n-1)/2,i 1≦i≦(n−1)/2,i 与 i + ( n + 1 ) / 2 i+(n+1)/2 i+(n+1)/2 连线。同时, 0 0 0 分别与 ( n − 1 ) / 2 (n-1)/2 (n−1)/2 和 ( n + 1 ) / 2 (n+1)/2 (n+1)/2 连线。

定理3 设 G G G是 ( n , m ) (n, m) (n,m)单图,若 δ ( G ) ≥ ⌊ n 2 ⌋ \delta(G)\geq\left\lfloor\frac{\mathrm{n}}{2}\right\rfloor δ(G)≥⌊2n⌋,则 G G G连通。


定理4 设 G G G是 ( n , m ) (n, m) (n,m)单图,若对任意正整数 k k k ,有: δ ( G ) ≥ n + k − 2 2 \delta\left(G\right)\geq\frac{n+k-2}2 δ(G)≥2n+k−2 则 G G G是 k k k连通的。
删除了 k − 1 k-1 k−1 个顶点的 H H H,在 H H H 中的最小度一定大于等于在 G G G 的最小度基本上减去 k - 1,等于的情况就是直接在 G G G 的最小度点再删去 k - 1条边。 如此都能推出 H H H 连通,因此原图 k k k 连通

注意: 最后说 H H H 连通,是因为, n − k + 1 n - k + 1 n−k+1 是 H H H 的点数
定理5 设 G G G是 n n n阶单图,若 δ ( G ) ≥ ⌊ n 2 ⌋ \delta\left(G\right)\geq\left\lfloor\frac n2\right\rfloor δ(G)≥⌊2n⌋ 则有: λ ( G ) = δ ( G ) \lambda(G)=\delta(G) λ(G)=δ(G)

(二)、描述连通性的其它参数简介(内容拓展)
三、图的宽直径简介
(一)、敏格尔定理
敏格尔定理是图的连通性问题的核心定理之一, 它描述了图的连通度与连通图中不同点对间的不相交路的数目之间的关系。
定义1 设 u u u与 v v v是图 G G G的两个不同顶点, S S S表示 G G G的一个顶点子集或边子集,如果 u u u与 v v v不在 G − S G-S G−S的同一分支上,称 S S S分离 u u u和 v v v。

定理1 (敏格尔1902—1985) (1) 设 x x x与 y y y是图 G G G中的两个不相邻点,则 G G G中分离点 x x x与 y y y的最少点数等于独立的 ( x , y ) (x, y) (x,y)路的最大数目;
(2) 设 x x x与 y y y是图 G G G中的两个不同顶点,则 G G G中分离点 x x x与 y y y的最少边数等于 G G G中边不重的 ( x , y ) (x, y) (x,y)路的最大数目。

又在该图中,边不重的 ( x , y ) (x ,y) (x,y)路最大条数是 2 2 2,分离点 x x x与 y y y的最小边分离集是 x u 1 , x u 2 {xu_1, xu_2} xu1,xu2, 包含两条边。

定理2 (惠特尼1932) 一个非平凡的图 G G G 是 k ( k ≧ 2 ) k (k≧2) k(k≧2) 连通的,当且仅当 G G G 的任意两个顶点间至少存在 k k k 条内点不交的 ( u , v ) (u ,v) (u,v) 路。
证明: (必要性) 设 G G G 是 k ( k ≧ 2 ) k (k≧2) k(k≧2) 连通的, u u u 与 v v v 是 G G G 的两个顶点 。
如果 u u u 与 v v v 不相邻, U U U 为 G G G 的最小 u − − v u--v u−−v 分离集,那么有 ∣ U ∣ ≧ k ( G ) ≧ k |U|≧k(G)≧k ∣U∣≧k(G)≧k,于是由敏格尔定理,结论成立;
若 u u u 与 v v v 邻接,其中 e = u v e=uv e=uv,那么,容易证明: G − e G-e G−e 是 ( k − 1 ) (k-1) (k−1) 连通的。设 W W W 是 G − e G-e G−e 的最小 u — v u—v u—v 分离集,由敏格尔定理知, G − e G-e G−e 至少包含 k − 1 k-1 k−1 条内点不交的 u − − v u--v u−−v 路,即 G G G 至少包含 k k k 条内点不交的 u − − v u--v u−−v 路。
(充分性) 假设 G G G 中任意两个顶点间至少存在 k k k 条内部不交路。设 U U U 是 G G G 的最小顶点割,即 ∣ U ∣ = k ( G ) |U|=k (G) ∣U∣=k(G)。令 x x x 与 y y y 是 G − U G-U G−U 的处于不同分支的两个点。所以 U U U 是 x x x 与 y y y 的分离集,由敏格尔定理: ∣ U ∣ ≧ k |U|≧k ∣U∣≧k, 即证明 G G G 是 k k k 连通的。
推论1 对 k ≥ 2 k≥ 2 k≥2,图 G G G 是 k k k 连通的当且仅当 G G G 至少有 k + 1 k + 1 k+1 个点并且 G G G 中任意两个不同顶点间均存在 k k k 条内部不想交的路; G G G 是 k ( k ≧ 2 ) k (k≧2) k(k≧2) 连通的,当且仅当 G G G 的任意两个顶点间至少存在 k k k 条内点不交的 ( u , v ) (u ,v) (u,v) 路。


对于边连通度,有类似定理:
定理3 (惠特尼1932) 一个非平凡的图 G G G是 k ( k ≧ 2 ) k (k≧2) k(k≧2)边连通的,当且仅当 G G G的任意两个顶点间至少存在 k k k条边不重的 ( u , v ) (u ,v) (u,v)路。
推论 对于一个阶至少为 3 3 3的无环图 G G G,下面三个命题等价。
(1) G是2连通的;
(2) G中任意两点位于同一个圈上;
(3) G无孤立点,且任意两条边在同一个圈上。(通过去掉圈上 u , v u,v u,v 至少要去掉两个顶点来证明 2 连通)

(二)、图的宽直径相关概念
1、问题背景
分析评价互联网络的性能有多个指标,如网络的开销(通信与材料开销), 网络的容错性(连通性), 网络中信息传递的传输延迟等。
所谓传输延迟,又称为时间延迟,是指信息从源传到目的地所需要的时间。
如何度量网络的传输延迟?
信息从源到目的地需要经过若干中间站存储和转发。因此,信息传输延迟可以用图的顶点间距离来度量。当然,每条边的长度可以定义为1.
于是,网络的最大通信延迟可以通过图的直径来度量。图的直径定义为:
d ( G ) = max { d ( u , v ) ∣ u , v ∈ V ( G ) } d(G)=\max\left\{d(u,v)|u,v\in V(G)\right\} d(G)=max{d(u,v)∣u,v∈V(G)}
在信息的单路径传输中,分析通信延迟,只需要考虑网络的直径即可。
直径虽然能够刻画网络的通信延迟,但毕竟是在最坏情形下的通信延迟,而网络中大距离点对并不多,所以用直径对信息传输延迟进行描述,还有点不精细。于是,有如下平均距离的概念:
设 G G G是 n n n阶图 ( n ≧ 2 ) (n≧2) (n≧2), G G G的平均距离 μ ( G ) μ(G) μ(G)定义为:
μ ( G ) = 2 n ( n − 1 ) ∑ u , v ∈ V ( G ) d ( u , v ) \mu(G)=\frac2{n(n-1)}\sum_{u,v\in V(G)}d(u,v) μ(G)=n(n−1)2u,v∈V(G)∑d(u,v)
平均距离是网络信息平均传输延迟的度量。跟直径研究一样,平均距离问题也吸引很多学者的研究,有很多研究结果。
求平均距离的一个值得研究的方向是求平均距离算法复杂性。求平均距离的最著名的Fredman算法时间复杂性是 o ( v 2 + v m ) o(v2+vm) o(v2+vm);求直径最著名算法是Floyd算法,时间复杂性是 o ( v m ) o (v m) o(vm) .确定平均距离问题是否比确定所有距离容易?这还是一个没有完结的挑战性问题。
信息的单路径传输延迟用直径或平均距离刻画。但是,如果要一次传输的信息量较大,远远超出链路带宽,就需要所谓的分包传送。
所谓的分包传送,就是按照带宽要求,把信息在起点进行分割打包,每个信息小包按照若干内点不交路从起点传到终点。基于此,上世纪90年代初,D Frank等图论学者和一些计算机专家从图论角度对信息分包传送的若干问题展开研究。研究的典型问题是:
(1) 分包传送的通信延迟度量;
(2) 分包传送的路由选择,即网络中平行寻径算法;
(3) 互联网络的设计与网络结构分析问题;
(4) 基于分包传送下互联网络的容错分析。
2、宽直径相关概念
定义1 设 x , y ∈ V ( G ) , C w ( x , y ) x, y ∈V(G), C_w (x, y) x,y∈V(G),Cw(x,y)表示 G G G中 w w w条内点不交路的路族, w w w称为路族的宽度, C w ( x , y ) C_w (x, y) Cw(x,y)中最长路的路长成为该路族的长度,记为: l ( C w ( x , y ) ) l (C_w (x, y)) l(Cw(x,y))。

定义2 设 x , y ∈ V ( G ) x, y ∈V(G) x,y∈V(G), 定义 x x x与 y y y间所有宽度为 w w w的路族长度的最小值 d w ( x , y ) d_w( x , y) dw(x,y)为 x x x与 y y y间 w w w宽距离,即:
d w ( x , y ) = min { l ( C w ( u , v ) ) : ∀ C w ( u , v ) } d_w(x,y)=\min\left\{l(C_w(u,v)){:}\forall C_w(u,v)\right\} dw(x,y)=min{l(Cw(u,v)):∀Cw(u,v)}

在上图中, G G G的一个宽度为 3 3 3的 u , v u, v u,v间的距离为:
d 3 ( u , v ) = min { l ( C 3 ( u , v ) ) : ∀ C 3 ( u , v ) } = 3 d_3(u,v)=\min\left\{l(C_3(u,v)):\forall C_3(u,v)\right\}=3 d3(u,v)=min{l(C3(u,v)):∀C3(u,v)}=3
注: x x x与 y y y间长度等于 w w w宽距离的路族称为 x x x与 y y y间最优路族。所以,求 w w w宽距离,就是要找到最优路族。
定义3 设 G G G是 w w w连通的, G G G的所有点对间的 w w w宽距离的最大值,称为 G G G的 w w w宽直径,记为 d w ( G ) d_w (G) dw(G)。即:
d w ( G ) = max { d ( x , y ) : x , y ∈ V ( G ) } d_w(G)=\max\begin{Bmatrix}d(x,y):x,y\in V(G)\end{Bmatrix} dw(G)=max{d(x,y):x,y∈V(G)}


注:从定义看出:对一般图来说,计算 w w w宽直径是一件很困难的工作。对宽直径的研究,主要是两方面:一是对一般图而言,研究 w w w宽直径的界;二是根据各种互联网络的结构特征,确定其宽直径。当然,研究宽直径与图的其它不变量之间的关系也是一个很有意义的方向。
(三)、一些主要研究结果简介
经过10多年的研究,组合网络理论取得了很多有意义结果,同时也有许多公开性问题等待人们继续研究。
1、 一般图的 w w w宽直径
定理1 对于任意连通图 G G G, 有:
d ( G ) = d 1 ( G ) ≤ d 2 ( G ) ≤ ⋯ ≤ d 3 ( G ) d\left(G\right)=d_{1}\left(G\right)\leq d_{2}\left(G\right)\leq\cdots\leq d_{3}\left(G\right) d(G)=d1(G)≤d2(G)≤⋯≤d3(G)
定理2 设 G G G是 n n n阶 w w w连通图, w ≧ 2 w ≧2 w≧2。则: 2 ≤ d w ( G ) ≤ n − w + 1 2\leq d_w(G)\leq n-w+1 2≤dw(G)≤n−w+1 而且,上界和下界都能达到。
定理3 设 G G G是 n n n阶 w w w连通图, w ≧ 2 w ≧2 w≧2, G G G 满足如下条件:
d G ( x ) + d G ( y ) ≥ n + w − 1 , ∀ x , y ∈ V ( G ) d_G\left(x\right)+d_G\left(y\right)\geq n+w-1,\forall x,y\in V\left(G\right) dG(x)+dG(y)≥n+w−1,∀x,y∈V(G)
那么, d w ( G ) = 2 d_w(G)=2 dw(G)=2, 并且上面条件是紧的。
定理4 设 G G G是 w w w连通 w w w正则图, w ≧ 2 w ≧2 w≧2,那么:
d W ( G ) ≥ d ( G ) + 1 d_{_{W}}\left(G\right)\geq d\left(G\right)+1 dW(G)≥d(G)+1
定理5 设 G G G是 n n n阶 w w w连通 w w w正则无向图, w ≧ 3 w ≧3 w≧3,那么:
d w ( G ) ≤ ⌊ 1 2 n ⌋ d_w\left(G\right)\leq\left\lfloor\frac12n\right\rfloor dw(G)≤⌊21n⌋
2、 图运算与 w w w宽直径
定理1 设 G i G_i Gi是 w i w_i wi连通有向图, 且: r w i ( G ) ≤ d ( G i ) r_{w_i}\left(G\right)\leq d\left(G_i\right) rwi(G)≤d(Gi), 1 ≦ i ≦ m 1≦i≦m 1≦i≦m. 如果 G = G 1 × G 2 × ⋯ × G m , G=G_1\times G_2\times\cdots\times G_m, G=G1×G2×⋯×Gm, 那么: d w ( G ) ≤ max { ∑ i = 1 m d ( G j ) + 1 ; ∑ j ≠ i m d ( G j ) + d w i ( G i ) ; 1 ≤ i ≤ m } d_w\left(G\right)\leq\text{ max }\left\{\sum_{i=1}^{m}d\left(G_{j}\right)+1;\sum_{j\neq i}^{m}d\left(G_{j}\right)+d_{w_i}\left(G_{i}\right);1\leq i\leq m\right\} dw(G)≤ max {∑i=1md(Gj)+1;∑j=imd(Gj)+dwi(Gi);1≤i≤m}
注:该结果是由徐俊明得到的。
定理2 (1) 设 G i G_i Gi是阶至少为3的 w i w_i wi连通无向图, i = 1 , 2 , … , m i=1, 2, …, m i=1,2,…,m。如果 G = G 1 × G 2 × ⋯ × G m G=G_1\times G_2\times\cdots\times G_m G=G1×G2×⋯×Gm ,且 w = w 1 + w 2 + … + w m w=w_1+w_2+…+w_m w=w1+w2+…+wm,则: d w ( G 0 ) ≤ max { ∑ j ≠ i m d ( G j ) + d w i ( G i ) ; 1 ≤ i ≤ m } {d}_{_{w}}\left(G_{0}\right)\leq\text{max}\left\{\sum_{j\neq i}^{m}d\left(G_{j}\right)+d_{_{w_{i}}}\left(G_{i}\right);1\leq i\leq m\right\} dw(G0)≤max{∑j=imd(Gj)+dwi(Gi);1≤i≤m}
(2) 设 G G G是 w ≧ 2 w≧2 w≧2连通无向图.如果 d w ( G ) = d ( G ) + 1 d_w(G)=d(G)+1 dw(G)=d(G)+1,则: d 1 + w ( K 2 × G ) ≤ d ( G ) + 2 d_{1+w}(K_2\times G)\leq d(G)+2 d1+w(K2×G)≤d(G)+2
注:该结果是由徐俊明得到的。
3、 图参数与w宽直径
定理1 设 G G G是 w w w连通无向图, w ≧ 2 w≧2 w≧2, 且 α ( G ) α(G) α(G)是 G G G的独立数。则 d W ( G ) ≤ 2 α ( G ) d_{_W}(G)\leq2\alpha(G) dW(G)≤2α(G)
4、宽直径与容错直径
容错直径的概念是由Krishnamoorthy等在1987年提出的,它是度量容错网络的最大通信延迟的量。即一个网络G,如果F是它的一个容错顶点集合,则G-F是连通的,它有一个确定直径,容错直径就是基于这样的背景提出的。
定义1 设 G G G是 w w w连通无向图, 则对 V ( G ) V(G) V(G)的任意子集 F F F,如果有 ∣ F ∣ < w |F|<w ∣F∣<w, 定义 G G G的 w − 1 w-1 w−1容错直径 D w ( G ) D_w(G) Dw(G)为: D w ( G ) = max { d ( G − F ) ∣ ∀ F ⊂ V ( G ) , ∣ F ∣ < w } D_w(G)=\max\left\{d(G-F)\big|\forall F\subset V(G),\big|F\big|<w\right\} Dw(G)=max{d(G−F) ∀F⊂V(G), F <w}
从容错直径的定义可以看出,计算图的容错直径跟宽直径一样,非常困难,事实上,是NP完全问题。因此,对容错直径的研究,自然转移到对容错直径和宽直径之间的关系进行研究。
定理1 设 G G G是 w w w连通无向图, w ≧ 2 w≧2 w≧2, 则有: D w ( G ) ≤ d w ( G ) D_w(G)\leq d_w(G) Dw(G)≤dw(G)
定理2 设 G G G是直径为 d d d的 2 2 2连通图,则:
d 2 ( G ) ≤ max { ( d − 1 ) ( D 2 − 1 2 d − 1 ) + 1 , D 2 + 1 } \begin{aligned}d_2\left(G\right)\leq\max\left\{(d-1)\bigg(D_2-\frac{1}{2}d-1\bigg)+1,D_2+1\right\}\end{aligned} d2(G)≤max{(d−1)(D2−21d−1)+1,D2+1}
定理3 设 G G G是 2 2 2连通无向图, 则有:
d 2 ( G ) ≤ { D 2 + 1 , 若 d = 2 ; ( d − 1 ) ( D 2 − 1 ) , 若 d ≥ 3 d_2(G)\leq\begin{cases}D_2+1,\text{若 }d=2;\\(d-1)(D_2-1),\text{若 }d\geq3\end{cases} d2(G)≤{D2+1,若 d=2;(d−1)(D2−1),若 d≥3
定理4 设 G G G是直径为 2 2 2的 2 2 2连通图,则: d 2 = D 2 + 1 d_2=D_2+1 d2=D2+1 的充分必要条件为 d 2 = 3 d_2=3 d2=3 或 d 2 = 4 d_2=4 d2=4, 且达到 d 2 d_2 d2 值的任何两点必然邻接。
注:关于容错直径和宽直径的关系研究文章不是很多,主要是徐俊明发表的文章。
5、 典型网络的w宽直径
经过近20年的研究,已经确定出很多著名网络的容错直径与宽直径,下面做总结性介绍。
(1) 超立方体网络 Q n Q_n Qn
k ( Q n ) = n d ( Q n ) = n k\left(Q_n\right)=n\quad d\left(Q_n\right)=n k(Qn)=nd(Qn)=n
d w ( Q n ) = D w ( Q n ) = { n , 若 w ≤ n − 1 n + 1 , 若 w = n . d_w(Q_n)=D_w(Q_n)=\begin{cases}n,\text{若 }w\leq n-1\\n+1,\text{若 }w=n.&\end{cases} dw(Qn)=Dw(Qn)={n,若 w≤n−1n+1,若 w=n.
(2) de Brujin 有向网络 B ( d , n ) ( d ≧ 2 , n ≧ 1 ) B(d , n) (d≧2, n≧1) B(d,n)(d≧2,n≧1)
k ( B ( d , n ) ) = d − 1 d ( B ( d , n ) ) = n k\left(B(d,n)\right)=d-1\quad\quad\quad\quad\quad\quad\quad\quad d\left(B(d,n)\right)=n k(B(d,n))=d−1d(B(d,n))=n
d w ( B ( d , n ) ) = D w ( B ( d , n ) ) = n + 1 , 若 w ≤ d − 1 d_{_w}(B(d,n))=D_{_w}(B(d,n))=n+1,\text{若}w\leq d-1 dw(B(d,n))=Dw(B(d,n))=n+1,若w≤d−1
(3) Kautz 有向网络 K ( d , n ) ( d ≧ 2 , n ≧ 1 ) K(d , n) (d≧2, n≧1) K(d,n)(d≧2,n≧1)
k ( K ( d , n ) ) = d d ( K ( d , n ) ) = n k\left(K\left(d,n\right)\right)=d\quad\quad\quad\quad\quad\quad d\left(K\left(d,n\right)\right)=n k(K(d,n))=dd(K(d,n))=n
d w ( K ( d , n ) ) ≤ { n + 1 , 若 w ≤ d − 2 n + 2 , 若 w = d − 1 或 d d_{w}\left(K\left(d,n\right)\right)\leq\begin{cases}n+1,\text{若}w\leq d-2\\n+2,\text{若}w=d-1\text{或}d\end{cases} dw(K(d,n))≤{n+1,若w≤d−2n+2,若w=d−1或d
D w ( K ( d , n ) ) = d w ( K ( d , n ) ) = { n + 1 , 若 w ≤ d − 1 , 或 w = d 且 n = 2 ; n + 2 , 若 w = d 或 n ≥ 3 D_w(K(d,n))=d_w(K(d,n))=\begin{cases}n+1,\text{若}w\leq d-1,\text{或}w=d\text{且}n=2;\\n+2,\text{若}w=d\text{ 或}n\geq3&\end{cases} Dw(K(d,n))=dw(K(d,n))={n+1,若w≤d−1,或w=d且n=2;n+2,若w=d 或n≥3
(4) de Brujin 无向网络 U B ( d , n ) ( d ≧ 2 , n ≧ 1 ) UB (d , n) (d≧2, n≧1) UB(d,n)(d≧2,n≧1)
k ( U B ( d , n ) ) = 2 d − 2 d ( U B ( d , n ) ) = n k\left(UB\left(d,n\right)\right)=2d-2\quad\quad d\left(UB\left(d,n\right)\right)=n k(UB(d,n))=2d−2d(UB(d,n))=n
d d − 1 ( U B ( d , n ) ) ≤ n + 1 d_{d-1}(UB(d,n))\leq n+1 dd−1(UB(d,n))≤n+1
D 2 ( U B ( 2 , n ) ) = d 2 ( U B ( 2 , n ) ) = n D_2(UB(2,n))=d_2(UB(2,n))=n D2(UB(2,n))=d2(UB(2,n))=n
(5) 无向超环面 C ( d 1 , d 2 , … , d m ) C (d_1,d_2 ,…, d_m) C(d1,d2,…,dm)
k ( C ( d 1 , d 2 , ⋯ , d m ) ) = 2 m k\left(C\left(d_1,d_2,\cdots,d_m\right.\right))=2m k(C(d1,d2,⋯,dm))=2m
d ( C ( d 1 , d 2 , ⋯ , d m ) ) = ∑ i = 1 m ⌊ 1 2 d i ⌋ d\left(C\left(d_{1},d_{2},\cdots,d_{m}\right.\right))=\sum_{i=1}^{m}\left\lfloor\frac12d_{i}\right\rfloor d(C(d1,d2,⋯,dm))=i=1∑m⌊21di⌋
令 G = C ( d 1 , d 2 , … , d m ) G = C (d_1,d_2 ,…, d_m) G=C(d1,d2,…,dm)
d 2 m ( G ) = { 2 d ( G ) − 1 , 若 G = C 2 w + 1 × C 3 , w ≥ 2 ; 2 d ( G ) − 2 , 若 G = C 2 w + 2 × C 3 , w ≥ 2 ; d ( G ) + 2 , 若 G = C d × C 4 , d ≥ 9 ; d ( G ) + 2 , 若 G = C d × C 5 , 9 ≤ d ≤ 1.3 ; d ( G ) + 1 , 其他。 d_{_{2m}}(G)=\begin{cases}2d\left(G\right)-1,\text{若 }G=C_{_{2w+1}}\times C_{_{3}},w\geq2;\\2d\left(G\right)-2,\text{若 }G=C_{_{2w+2}}\times C_{_{3}},w\geq2;\\d\left(G\right)+2,\text{若 }G=C_{_{d}}\times C_{_{4}},d\geq9;\\d\left(G\right)+2,\text{若 }G=C_{_{d}}\times C_{_{5}},9\leq d\leq1.3;\\d\left(G\right)+1,\text{其他。}&\end{cases} d2m(G)=⎩ ⎨ ⎧2d(G)−1,若 G=C2w+1×C3,w≥2;2d(G)−2,若 G=C2w+2×C3,w≥2;d(G)+2,若 G=Cd×C4,d≥9;d(G)+2,若 G=Cd×C5,9≤d≤1.3;d(G)+1,其他。
(6) 有向超环面 C ⃗ ( d 1 , d 2 , ⋯ , d m ) \vec{C}\left(d_{1},d_{2},\cdots,d_{m}\right) C(d1,d2,⋯,dm)
d n ( C ⃗ ) = ∑ i = 1 n ( d i − 1 ) = d ( C ⃗ ) + 1 d_n\left(\vec{C}\right)=\sum_{i=1}^n\left(d_i-1\right)=d\left(\vec{C}\right)+1 dn(C)=i=1∑n(di−1)=d(C)+1
如果 d 1 = d 2 = … = d n = d d_1=d_2=…=d_n=d d1=d2=…=dn=d, 则:
d n ( C ⃗ n ( d ) = d ( C ⃗ n ( d ) ) = n ( d − 1 ) + 1 d_n(\vec{C}_n(d)=d\left(\vec{C}_n(d)\right)=n(d-1)+1 dn(Cn(d)=d(Cn(d))=n(d−1)+1
D n ( C ⃗ n ( d ) ) = d w ( C ⃗ n ( d ) ) = { n ( d − 1 ) , 若 1 ≤ w ≤ n − 1 n ( d − 1 ) + 1 , 若 w = n D_n\left(\vec{C}_n(d)\right)=d_w\left(\vec{C}_n(d)\right)=\begin{cases}n(d-1),\text{若}1\leq w\leq n-1\\n(d-1)+1,\text{若}w=n&\end{cases} Dn(Cn(d))=dw(Cn(d))={n(d−1),若1≤w≤n−1n(d−1)+1,若w=n
(7) 广义超立方体网络 Q ( d 1 , d 2 , … , d n ) Q (d_1,d_2,…,d_n) Q(d1,d2,…,dn)

(8) 立方连通圈CCC(n)
k ( C C C ( n ) ) = 3 k\left(CCC\left(n\right)\right)=3 k(CCC(n))=3
d ( C C C ( n ) ) = ⌊ 5 2 n − 1 ⌋ d\left(CCC(n)\right)=\left\lfloor\frac52n-1\right\rfloor d(CCC(n))=⌊25n−1⌋
d 3 ( C C C ( n ) ) = D 3 ( C C C ( n ) ) = ⌊ 5 2 n + 2 ⌋ d_3(CCC(n))=D_3(CCC(n))=\left\lfloor\frac52n+2\right\rfloor d3(CCC(n))=D3(CCC(n))=⌊25n+2⌋

这篇关于【图论及其运用 — 电子科技大学】(三)第三章 图的连通性的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!