4th专题
微分方程（Blanchard Differential Equations 4th）中文版Section6.3
二阶线性方程 Laplace 变换求解 在这一节中，我们将拉普拉斯变换方法扩展到二阶常系数强迫线性方程，即具有以下形式的方程： d 2 y d t 2 + p d y d t + q y = f ( t ) ， \frac{d^2 y}{dt^2} + p \frac{dy}{dt} + qy = f(t)， dt2d2y+pdtdy+qy=f(t)， 其中 p p p 和 q q
微分方程（Blanchard Differential Equations 4th）中文版Section5.1
平衡点分析 从第3章的工作中，我们能够对线性系统的解有定性和解析的理解。不幸的是，非线性系统通常不容易使用我们开发的解析和代数技术来分析，但我们可以利用线性系统的数学来理解非线性系统在其平衡点附近的行为。 Van der Pol 方程 为了说明如何分析平衡点附近解的行为，我们从一个简单但重要的非线性系统——Van der Pol 系统开始。回顾一下，Van der Pol 系统是： d x
微分方程（Blanchard Differential Equations 4th）中文版Section4.4
稳态的振幅和相位系统 在本节中，我们回到方程 d 2 y d t 2 + p d y d t + q y = cos ω t \frac{d^2 y}{dt^2} + p \frac{dy}{dt} + qy = \cos \omega t dt2d2y+pdtdy+qy=cosωt 用于周期性强迫的阻尼谐振子。我们的目标是建立解决方案行为与参数之间的定量关系——特别是决定强迫频率
微分方程（Blanchard Differential Equations 4th）中文版Section3.5
特殊情况: 重根和零特征值的线性系统 在前面的三节中，我们讨论了线性系统 d Y d t = A Y \frac{dY}{dt} = AY dtdY=AY 其中 2 × 2 2 \times 2 2×2 矩阵 A A A 具有两个不同的非零实特征值或一对复共轭特征值。在这些情况下，我们能够使用特征值和特征向量来草绘 x y xy xy 相平面的解，绘制 x ( t ) x(t)
微分方程（Blanchard Differential Equations 4th）中文版Section2.3
阻尼谐振子 在本节中，我们将描述一种解析技术，它适用于本书中最重要的模型之一——阻尼谐振子。这一二阶微分方程用于建模各种现象，如质量-弹簧系统、电路理论中的RLC电路，以及人体的血糖调节系统。 例如，考虑汽车的悬挂系统。它可以平滑崎岖道路上的颠簸，并帮助保持轮胎与地面的接触。我们主要关注悬挂中的弹簧和减震器（见图2.34和2.35）。弹簧吸收由路面颠簸引起的力，并保持轮胎与道路接触。减震器由一
【4th chapter】信息安全技术—安全技术、安全架构、安全策略、安全管理、软件的脆弱性
概要 安全技术安全架构安全策略安全管理软件的脆弱性加密技术（Encryption Technology）安全域架构（Security Domain Architecture）访问控制策略（Access Control Policy）信息安全管理体系（Information Security Management System, ISMS）缓冲区溢出（Buffer Overflow）防火墙（Fir
Learn HTML 4 In a Weekend, 4th Edition
版权声明：原创作品，允许转载，转载时请务必以超链接形式标明文章原始出版、作者信息和本声明。否则将追究法律责任。 http://blog.csdn.net/topmvp - topmvp Complete just the first two tutorial sessions to develop the HTML skills that you need to start creating
Practical Programming in Tcl and Tk (4th Edition)
版权声明：原创作品，允许转载，转载时请务必以超链接形式标明文章原始出版、作者信息和本声明。否则将追究法律责任。 http://blog.csdn.net/topmvp - topmvp Practical Programming in Tcl/Tk is described as the "bible" for Tcl programmers. It is a guide to the Tcl
Sams Teach Yourself JavaScript in 24 Hours (4th Edition)
版权声明：原创作品，允许转载，转载时请务必以超链接形式标明文章原始出版、作者信息和本声明。否则将追究法律责任。 http://blog.csdn.net/topmvp - topmvp JavaScript is one of the easiest, most straightforward ways to enhance a website with interactivity. Sams
Security in Computing (4th Edition)
版权声明：原创作品，允许转载，转载时请务必以超链接形式标明文章原始出版、作者信息和本声明。否则将追究法律责任。 http://blog.csdn.net/topmvp - topmvp A sweeping revision of the classic computer security text. This book provides end-to-end, detailed covera
Beginning XML, 4th Edition
版权声明：原创作品，允许转载，转载时请务必以超链接形式标明文章原始出版、作者信息和本声明。否则将追究法律责任。 http://blog.csdn.net/topmvp - topmvp Beginning XML provides a complete course in the Extensible Markup Language (XML) with an unusually grad
SDNU_ACM_ICPC_2020_Winter_Practice_4th
出题人：RYC 题目考察知识点： A：三分 B：矩阵快速幂 C：矩阵快速幂 D：思维 + 暴力构造 E：思维 F：计算几何 G：计算几何 H：水题/简单思维 I：水题/模拟 J：水题/模拟 K：水题/水题 L：水题/简单博弈 M：水题/暴力 考虑到两点原因，这次以及之后必补题就不放了. 1. 努力的人自然会补. 2. 队内三个人负责不同的模块，有些题不要求人人补，负责此知识点的
![[英语歌曲]七月四日：4th of July](http://www.chinadaily.com.cn/language_tips/auvideo/attachement/gif/site1/20071210/0013729e41a908c71ecb1d.gif)
[英语歌曲]七月四日：4th of July
我听之我见：近乎痴狂地去爱一个人，有多少人有过这样的经历？或许有人认为这只是傻，全是痴，嗤之以鼻，一笑而过。然而，不身处其中之人如何能解其中味？喜也好，悲也罢，敢这样不计得失地去爱的人都是有大勇气的。如果一生能有一次这么刻骨铭心的爱，便不枉此生了吧！ Download 英文歌词 4th of July
Algorithm 4th environment setup
algs4的官方给出环境搭建步骤较多，在github找了一下，看到了aistrate的repo，发现用这个非常方便。 [toc] 1. 材料与环境准备 1.1 代码与数据准备 mkdir ~/algs4wget http://algs4.cs.princeton.edu/code/algs4-data.zip unzip algs4-data.zipgit clon
Thinking In Java 4th Edition
[size=medium][color=indigo]“上帝赋予人类说话的能力，而言语又创造了思想，思想是人类对宇宙的量度。” ——摘自《Prometheus Unbound》，Shelley • 人类……极其受那些已经成为社会表达工具的特定语言的支配。想像一下，如果一个人可以不使用语言就能够从本质上适应现实世界，语言仅仅是解决具体的交流和反映问题时
CARLA 笔记（4th）— 基础模块使用（client、world、Actor 与 Blueprint、搭建Sensor、Camera、Lidar 构建、观察者放置）
3. 搭建传感器 Sensor Sensor 是一种特殊的 Actor，它的蓝图也是可以在蓝图库里边找到的，目前 Carla 已经支持了很多传感器，比如 摄像头： Depth， RGB ， Semantic segmentation探测器： Collision ， Lane invasion ， Obstacle其他： GNSS ， IMU ， LIDAR raycast ， Radar 传
Algorithms,4th(算法) IntelliJ上路指南（Windows）
对于新手来说，我推荐使用IntelliJ来学习Algorithms中的算法，同时也是官方直接提供安装教程的方法，大家可以参考官方教程来进行安装。以下是我总结的安装过程与注意事项。 1.官方一键安装 https://lift.cs.princeton.edu/java/windows/ 在以上网址中有集成的安装包，一键傻瓜式安装包，有详细教程。 2.IDEA的配置 1.打开项目 注意的问题
求助: thinkpad x1 carbon 4th 2016 版 安装ubuntu 14.04 问题？
在thinkpad技术支持下， 先是设置了bios 选择Security—Secure Boot—Disabled，再进入Startup—UEFI/Legacy Boot选项，UEFI/Legacy Boot设置为Legacy only，最后再按F10（Fn+F10）选择YES保存退出。 但是一直黑屏， 无法继续， 网上查找，得知 需要设置intel_pstate=no_hwp， 设置后
Real-Time Rendering 4th 译文《三 图形处理单元》
第三章 图形处理单元 从历史上来看，图形学的加速发展是与处理三角形重叠的像素扫描线上进行颜色插值，然后显示这些值开始的，其中包括访问能够让纹理应用到物体表面的图像数据的能力，其中还添加了用于插值和测试z深度的硬件，由于它们的频繁使用，因此将此类过程用于专用硬件以提高性能。连续几代硬件中添加了渲染管线的更多部分，以及每个部分的更多功能。专用图形硬件相对于CPU的唯一计算优势是速度，但速度至关重要。
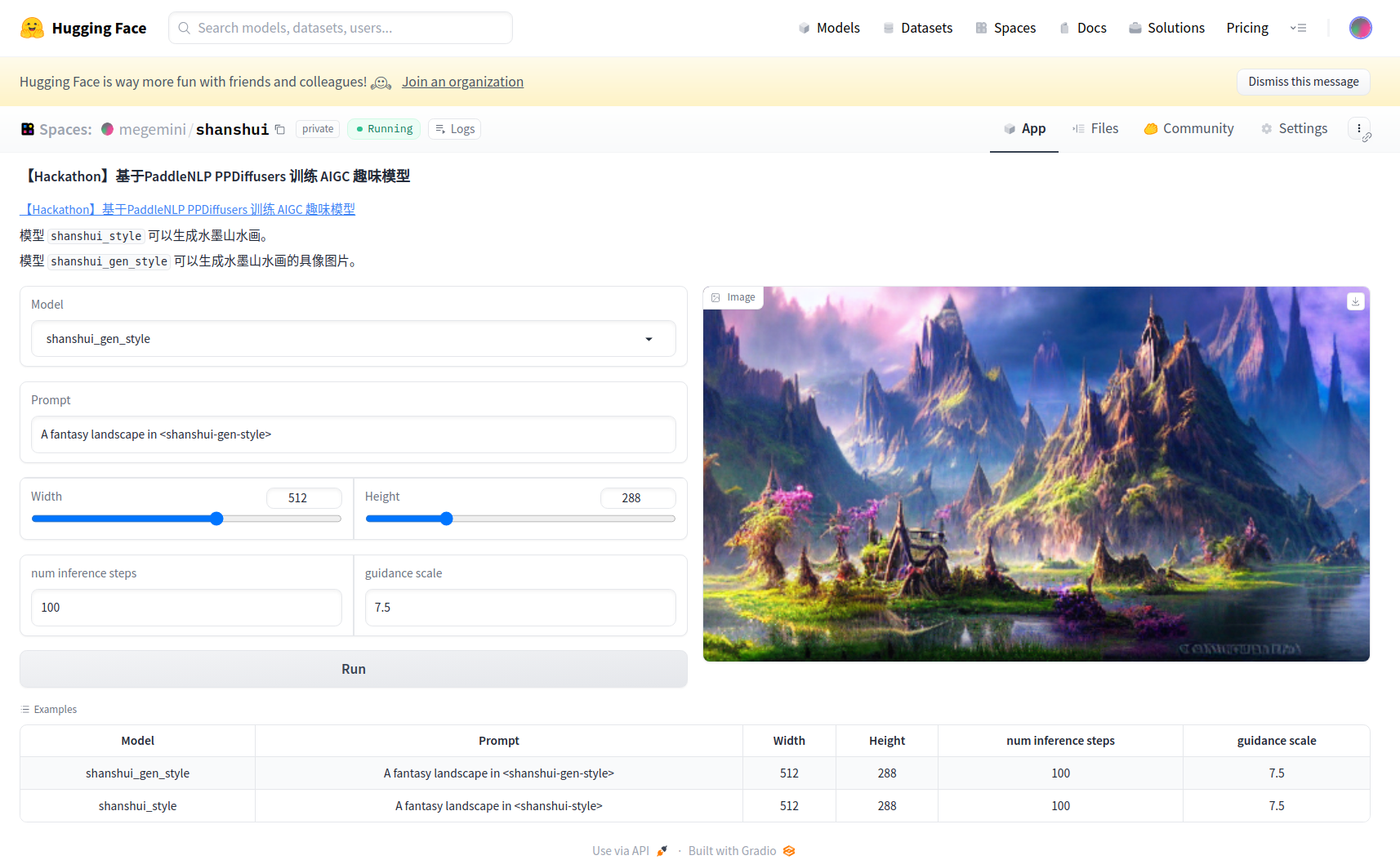
【Hackathon 4th AIGC】当中国水墨山水遇上AIGC
★★★ 本文源自AlStudio社区精品项目，【点击此处】查看更多精品内容 >>> 【PaddlePaddle Hackathon 第四期】No.105 作品提交 活动链接 👉 No.105：基于PaddleNLP PPDiffusers 训练 AIGC 趣味模型 【队名】：megemini 【模型简介】：当中国水墨山水遇上AIGC 【模型链接】：Hugging Face 地址: 模型 �
learning python下载_Learning Python 4th Edition-Oreilly 英文pdf格式
内容介绍热点排行相关文章下载地址↓ Learning Python 4th Edition《Python学习手册（第4版）》学习Python的主要内建对象类型：数字、列表和字典。使用Python语句创建和处理对象，并且学习Python的通用语法模型。使用函数构造和重用代码，函数是Python的基本过程工具。学习Python模块：封装语句、函数以及其他工具，以便构建较大的组件。学习Python的面