题目来源：POJ 2356 Find a multiple 题意：n个数 选出任意个数 使得这些数的和是n的倍数 思路：肯定有解 并且解是连续的一段数 证明： 假设有m个数 a1,a2,a3...am    s1 s2 s3...sm为前缀和 s1 = a1 s2 = a1+a2 s3 = a1+a2+a3... sm = a1+a2+a3+...+am 1.如果某个前缀和si%m =

和poj 3370很像， 但这里只有一个n且对应n个数 根据鸽巢原理是应该存在一个i对应前i项和模n==0 但是题目中说了这n个数可以相同，所以可能存在不等于0的情况 比如： 5 1 5 5 5 5 但此时必然sum%n有重复 同poj 3370一样输出相同两数对应下标之间的数即可 代码如下： #include <cstdio>#include <cstring>#def

判断一组数中是否存在和整除c的子集，若存在输出子集中元素对应下标 否则输出no sweets 取sum为第1个到当前第i堆糖果的集合 令tmp = sum%c 则在i从1到n的过程中，因为n>=c 当n>c时根据鸽巢原理tmp必然重复 我们可以简单的取重复之间的所有数 而当n==c时只需取1-使得tmp == 0之间（包括边界）的下标即可 可以得知此题恒有解 代码如下： #

题目的意思是对于一个n位数，删除m个位后，得到的最小数是什么，比如12345 2,删除两个位，得到最小的就是123.实际上这题目解法很多，好像有贪心，线段树，RMQ等，因为我最近在学习RMQ，所以就用RMQ了。 这题目用了一个鸽巢原理,得到的m-n位数的第一位，必然出现在1~m-n+1,这个由鸽巢原理就十分明显了（如果1~n-(m-n)+1都没有的话，剩下的m-n-1个位是不可能凑出m-n个位的

解梯报告 题目链接 ：http://poj.org/problem?id=3370 题目大意 ：给你n个数，找出其中c个数满足c个数的和是c的倍数。（c <=n） 思路 ：余数计算 + 鸽巢定理。             取余是一种常用手段，尤其是当题目中找一些数字直接和的关系的时候，往往通过             余数来将数字分类。2011年多校FZU有一位dp的题目就可以用余数乱搞

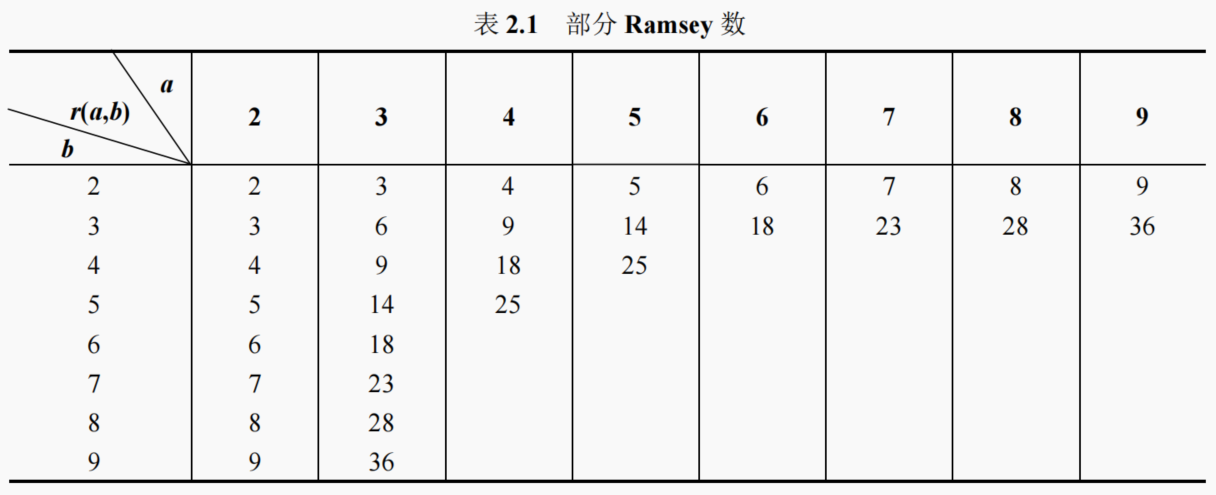
目录 1. 容斥原理容斥原理三种形式 2. 容斥原理应用有限重复数的多重集合的 r 组合数错排问题 3. 鸽巢原理4. Ramsey 定理 1. 容斥原理 容斥原理提供了一种通过计算每个单独集合的大小，然后修正重复计数的方法，从而得到多个集合并集大小的计算方法。它通过减去每个交集的元素个数，再加上每两个集合的交集，再减去每三个集合的交集，以此类推，来避免多重计数。 定理 1.

http://162.105.81.212/JudgeOnline/problem?id=3370 http://162.105.81.212/JudgeOnline/problem?id=2356   定理：如果n+1个物体被放进n个盒子，那么至少有一个盒子包含两个或更多个物体。 应用：给定n个数a1,a2,...,an.则比存在整数k和l（0<=k<l<=n)）使得a[k+1]+a[k

文章目录 第3章 容斥原理与鸽巢原理3.1 De Morgan定理3.2 容斥定理3.3 容斥原理举例3.4 容斥原理的应用3.5 n对夫妻问题3.6 错排问题3.7 棋盘多项式和有禁区的排列3.8 有限制的排列3.9 鸽巢原理3.9.1 整除问题3.9.2 图形问题3.9.3 连续累加问题 第3章 容斥原理与鸽巢原理 3.1 De Morgan定理 德摩根（De Morg

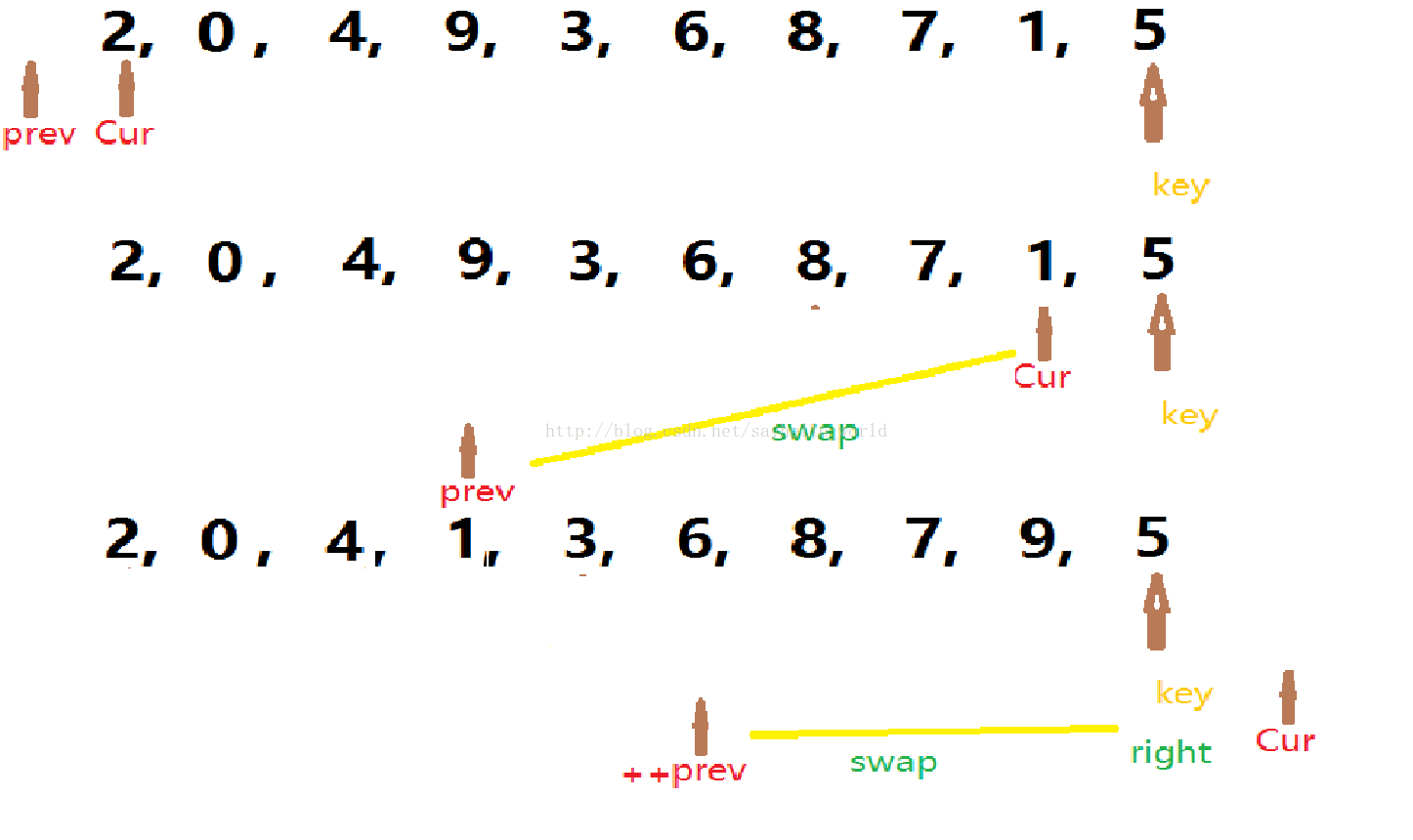
插入排序以及选择排序请查阅我往期博客：http://blog.csdn.net/sayhello_world/article/details/61927082 冒泡排序： 思想：两两交换，大的放到后面。重复size-1次 代码实现： [cpp]  view plain copy //冒泡排序   void Bubble_Sort(int