本文主要是介绍组合数学_第3章_容斥原理与鸽巢原理,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 第3章 容斥原理与鸽巢原理
- 3.1 De Morgan定理
- 3.2 容斥定理
- 3.3 容斥原理举例
- 3.4 容斥原理的应用
- 3.5 n对夫妻问题
- 3.6 错排问题
- 3.7 棋盘多项式和有禁区的排列
- 3.8 有限制的排列
- 3.9 鸽巢原理
- 3.9.1 整除问题
- 3.9.2 图形问题
- 3.9.3 连续累加问题
第3章 容斥原理与鸽巢原理
3.1 De Morgan定理
德摩根(De Morgan)定理:若 A A A和 B B B是集合 U U U的子集,则
-
A ∪ B ‾ = A ‾ ∩ B ‾ \overline{A\cup B}=\overline{A} \cap \overline{B} A∪B=A∩B
-
A ∩ B ‾ = A ‾ ∪ B ‾ \overline{A\cap B}=\overline{A} \cup \overline{B} A∩B=A∪B
德摩根定理的推广:
- A 1 ∪ A 2 ∪ ⋯ ∪ A n ‾ = A 1 ‾ ∩ A 2 ‾ ∩ ⋯ ∩ A n ‾ \overline{A_1 \cup A_2 \cup \cdots \cup A_n }=\overline{A_1} \cap \overline{A_2} \cap \cdots \cap \overline{A_n} A1∪A2∪⋯∪An=A1∩A2∩⋯∩An
- A 1 ∩ A 2 ∩ ⋯ ∩ A n ‾ = A 1 ‾ ∪ A 2 ‾ ∪ ⋯ ∪ A n ‾ \overline{A_1 \cap A_2 \cap \cdots \cap A_n }=\overline{A_1} \cup \overline{A_2} \cup \cdots \cup \overline{A_n} A1∩A2∩⋯∩An=A1∪A2∪⋯∪An
3.2 容斥定理
∣ A ∪ B ∪ C ∣ = ∣ A ∣ + ∣ B ∣ + ∣ C ∣ − ∣ A ∩ B ∣ − ∣ A ∩ C ∣ − ∣ B ∩ C ∣ + ∣ A ∩ B ∩ C ∣ |A \cup B \cup C| =|A|+|B|+|C|-|A \cap B| - |A \cap C| - |B \cap C|+|A \cap B \cap C| ∣A∪B∪C∣=∣A∣+∣B∣+∣C∣−∣A∩B∣−∣A∩C∣−∣B∩C∣+∣A∩B∩C∣
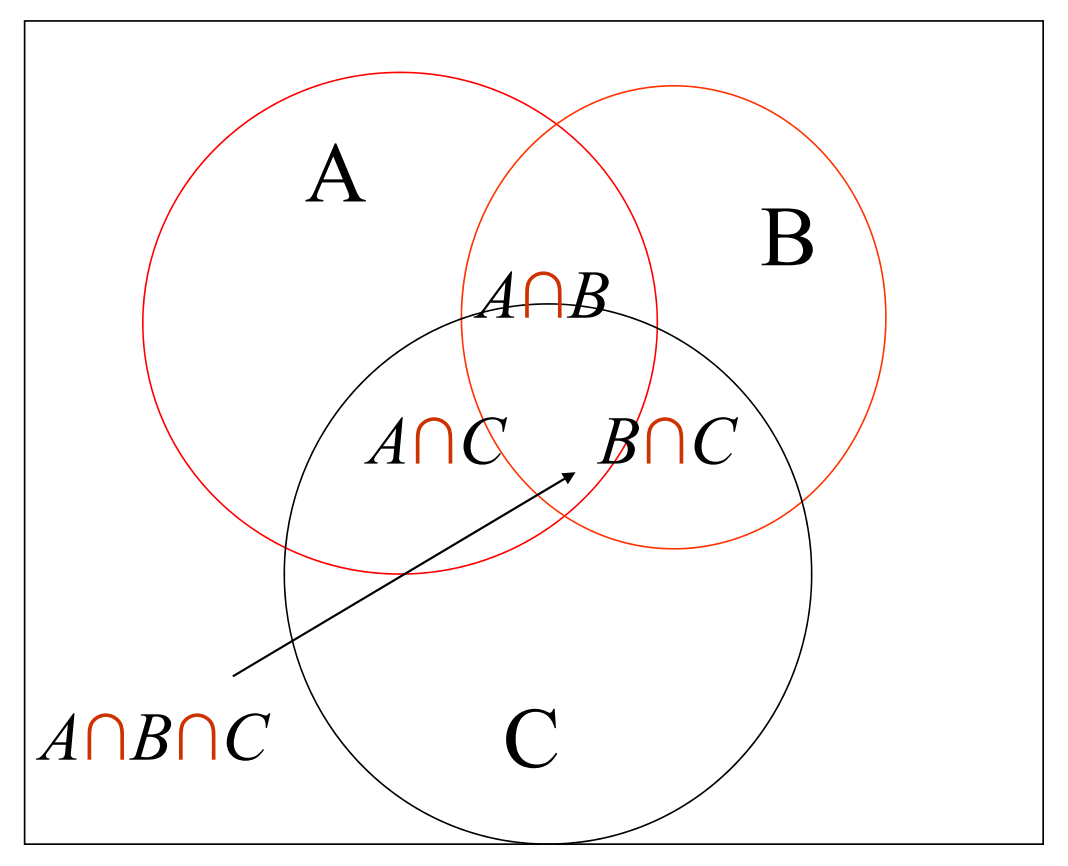
容斥原理的推广:
设 A 1 , A 2 , . . . A n A_1,A_2,...A_n A1,A2,...An是 n n n个有限的集合,则
∣ A 1 ∪ A 2 ∪ … ∪ A n ∣ = ∑ i = 1 n ∣ A i ∣ − ∑ i = 1 n ∑ j > i ∣ A i ∩ A j ∣ + ∑ i = 1 n ∑ j > i ∑ k > j ∣ A i ∩ A j ∩ A k ∣ − … + ( − 1 ) n − 1 ∣ A 1 ∩ A 2 ∩ … ∩ A n ∣ |A_1 \cup A_2 \cup \ldots \cup A_n| =\sum_{i=1}^n\left|A_i\right| -\sum_{i=1}^n \sum_{j>i}\left|A_i \cap A_j\right| +\sum_{\mathrm{i}=1}^{\mathrm{n}} \sum_{\mathrm{j}>\mathrm{i}} \sum_{\mathrm{k}>\mathrm{j}}\left|\mathrm{A}_{\mathrm{i}} \cap A_j \cap A_k\right|-\ldots +(-1)^{n-1}\left|A_1 \cap A_2 \cap \ldots \cap A_n\right| ∣A1∪A2∪…∪An∣=i=1∑n∣Ai∣−i=1∑nj>i∑∣Ai∩Aj∣+i=1∑nj>i∑k>j∑∣Ai∩Aj∩Ak∣−…+(−1)n−1∣A1∩A2∩…∩An∣
∣ A 1 ‾ ∩ A 2 ‾ ∩ … ∩ A n ‾ ∣ = N − ∣ A 1 ∪ A 2 ∪ … ∪ A n ∣ |\overline{A_1} \cap \overline{A_2} \cap \ldots \cap \overline{A_n}|=N-|A_1 \cup A_2 \cup \ldots \cup A_n| ∣A1∩A2∩…∩An∣=N−∣A1∪A2∪…∪An∣
3.3 容斥原理举例
例题:求从1到600的整数中能被2、3、5除尽的数的个数和不能被2、3、5除尽的个数。
解:令A、B、C分别为从1到600的整数中被2、3、5除尽的数的集合。
∣ A ∣ = ⌊ 600 2 ⌋ = 300 , ∣ B ∣ = ⌊ 600 3 ⌋ = 200 , ∣ C ∣ = ⌊ 600 5 ⌋ = 120 |A|=\lfloor\frac{600}{2}\rfloor=300,|B|=\lfloor\frac{600}{3}\rfloor=200,|C|=\lfloor\frac{600}{5}\rfloor=120 ∣A∣=⌊2600⌋=300,∣B∣=⌊3600⌋=200,∣C∣=⌊5600⌋=120,
∣ A ∩ B ∣ = ⌊ 600 2 × 3 ⌋ = 100 , ∣ A ∩ C ∣ = ⌊ 600 2 × 5 ⌋ = 60 , ∣ B ∩ C ∣ = ⌊ 600 3 × 5 ⌋ = 40 |A \cap B|=\lfloor\frac{600}{2\times3}\rfloor=100,|A \cap C|=\lfloor\frac{600}{2\times5}\rfloor=60,|B \cap C|=\lfloor\frac{600}{3\times5}\rfloor=40 ∣A∩B∣=⌊2×3600⌋=100,∣A∩C∣=⌊2×5600⌋=60,∣B∩C∣=⌊3×5600⌋=40,
∣ A ∩ B ∩ C ∣ = ⌊ 600 2 × 3 × 5 ⌋ = 20 |A \cap B \cap C|=\lfloor\frac{600}{2\times3\times5}\rfloor=20 ∣A∩B∩C∣=⌊2×3×5600⌋=20,
被2、3,、5除尽的数的个数为
∣ A ∪ B ∪ C ∣ = ∣ A ∣ + ∣ B ∣ + ∣ C ∣ − ( ∣ A ∩ B ∣ − ∣ A ∩ C ∣ − ∣ B ∩ C ∣ ) + ∣ A ∩ B ∩ C ∣ = 300 + 200 + 120 − ( 100 + 60 + 45 ) − 20 = 400 |A \cup B \cup C| =|A|+|B|+|C| - (|A \cap B| - |A \cap C| - |B \cap C|)+|A \cap B \cap C| =300+200+120-(100+60+45)-20=400 ∣A∪B∪C∣=∣A∣+∣B∣+∣C∣−(∣A∩B∣−∣A∩C∣−∣B∩C∣)+∣A∩B∩C∣=300+200+120−(100+60+45)−20=400
不能被2、3,、5除尽的数的个数为
∣ A ‾ ∩ B ‾ ∩ C ‾ ∣ = N − ∣ A ∪ B ∪ C ∣ = 600 − 400 = 200 |\overline{A} \cap \overline{B} \cap \overline{C}|=N-|A \cup B \cup C|=600-400=200 ∣A∩B∩C∣=N−∣A∪B∪C∣=600−400=200
例题:求由a、b、c、d四个字母构成的 n n n位符号串中,a、b、c(每个)至少出现一次的符号串数目。
解:令A、B、C分别为 n n n位符号串中不出现a、b、c符号的集合。由于 n n n位符号串中每一位都可取a、b、c、d四种符号中的一个,故不允许出现a的 n n n位符号串的个数应是 3 n 3^n 3n,即 ∣ A ∣ = ∣ B ∣ = ∣ C ∣ = 3 n , ∣ A ∩ B ∣ = ∣ A ∩ C ∣ = ∣ B ∩ C ∣ = 2 n , ∣ A ∩ B ∩ C ∣ = 1 |A|=|B|=|C|=3^n,|A \cap B|=|A \cap C|=|B \cap C|=2^n,|A \cap B \cap C|=1 ∣A∣=∣B∣=∣C∣=3n,∣A∩B∣=∣A∩C∣=∣B∩C∣=2n,∣A∩B∩C∣=1,a、b、c每位都至少出现一次表示为 ∣ A ‾ ∩ B ‾ ∩ C ‾ ∣ |\overline{A} \cap \overline{B} \cap \overline{C}| ∣A∩B∩C∣,
∣ A ‾ ∩ B ‾ ∩ C ‾ ∣ = 4 n − ( ∣ A ∣ + ∣ B ∣ + ∣ C ∣ ) + ( ∣ A ∩ B ∣ + ∣ A ∩ C ∣ + ∣ C ∩ B ∣ ) − ∣ A ∩ B ∩ C ∣ = 4 n − 3 ⋅ 3 n + 3 ⋅ 2 n − 1 |\overline{A} \cap \overline{B} \cap \overline{C}| = 4^n-(|A|+|B|+|C|)+(|A \cap B|+|A \cap C|+|C \cap B|)-|A \cap B \cap C| = 4^n-3 \cdot 3^n+3 \cdot 2^n-1 ∣A∩B∩C∣=4n−(∣A∣+∣B∣+∣C∣)+(∣A∩B∣+∣A∩C∣+∣C∩B∣)−∣A∩B∩C∣=4n−3⋅3n+3⋅2n−1
3.4 容斥原理的应用
例题:对问题 x 1 + x 2 + x 3 = 15 , 0 ≤ x 1 ≤ 5 , 0 ≤ x 2 ≤ 6 , 0 ≤ x 3 ≤ 7 x_1+x_2+x_3=15,0\le x_1\le5,0\le x_2\le6,0\le x_3\le7 x1+x2+x3=15,0≤x1≤5,0≤x2≤6,0≤x3≤7,求整数解的数目。
解:如果没有 0 ≤ x 1 ≤ 5 , 0 ≤ x 2 ≤ 6 , 0 ≤ x 3 ≤ 7 0\le x_1\le5,0\le x_2\le6,0\le x_3\le7 0≤x1≤5,0≤x2≤6,0≤x3≤7,记所求的整数解的集合为 S S S, ∣ S ∣ = C 3 + 15 − 1 15 = C 17 2 = 136 |S|=C_{3+15-1}^{15}=C_{17}^{2}=136 ∣S∣=C3+15−115=C172=136。
分别设 S S S中满足 x 1 ≥ 6 x_1 \ge 6 x1≥6的子集为 A 1 A_1 A1,满足 x 2 ≥ 7 x_2 \ge 7 x2≥7的子集为 A 2 A_2 A2,满足 x 3 ≥ 8 x_3 \ge 8 x3≥8的子集为 A 3 A_3 A3,问题转化为求 ∣ A 1 ‾ ∩ A 2 ‾ ∩ A 3 ‾ ∣ |\overline{A_1} \cap \overline{A_2} \cap \overline{A_3}| ∣A1∩A2∩A3∣。
对于 A 1 A_1 A1,相当于 x 1 + x 2 + x 3 = 15 − 6 x_1+x_2+x_3=15-6 x1+x2+x3=15−6,即 x 1 + x 2 + x 3 = 9 x_1+x_2+x_3=9 x1+x2+x3=9,求其非负整数解得 ∣ A 1 ∣ = C 3 + 9 − 1 9 = 55 |A_1|=C_{3+9-1}^{9}=55 ∣A1∣=C3+9−19=55。
同理得 ∣ A 2 ∣ = C 3 + 8 − 1 8 = 45 , ∣ A 3 ∣ = C 3 + 7 − 1 7 = 36 |A_2|=C_{3+8-1}^{8}=45,|A_3|=C_{3+7-1}^{7}=36 ∣A2∣=C3+8−18=45,∣A3∣=C3+7−17=36
∣ A 1 ∩ A 2 ∣ = C 3 + ( 15 − 6 − 7 ) − 1 15 − 6 − 7 = C 4 2 = 6 |A_1 \cap A_2|=C_{3+(15-6-7)-1}^{15-6-7}=C_{4}^{2}=6 ∣A1∩A2∣=C3+(15−6−7)−115−6−7=C42=6
∣ A 1 ∩ A 3 ∣ = C 3 + ( 15 − 6 − 8 ) − 1 15 − 6 − 8 = C 3 2 = 3 |A_1 \cap A_3|=C_{3+(15-6-8)-1}^{15-6-8}=C_{3}^{2}=3 ∣A1∩A3∣=C3+(15−6−8)−115−6−8=C32=3
∣ A 1 ∩ A 2 ∣ = C 3 + ( 15 − 7 − 8 ) − 1 15 − 7 − 8 = C 2 2 = 1 |A_1 \cap A_2|=C_{3+(15-7-8)-1}^{15-7-8}=C_{2}^{2}=1 ∣A1∩A2∣=C3+(15−7−8)−115−7−8=C22=1
∣ A 1 ∩ A 2 ∩ A 3 ∣ = 0 |A_1 \cap A_2 \cap A_3|=0 ∣A1∩A2∩A3∣=0
∣ A 1 ‾ ∩ A 2 ‾ ∩ A 3 ‾ ∣ = 139 − ( 55 + 45 + 36 ) + ( 6 + 3 + 1 ) − 0 = 10 |\overline{A_1} \cap \overline{A_2} \cap \overline{A_3}|=139-(55+45+36)+(6+3+1)-0=10 ∣A1∩A2∩A3∣=139−(55+45+36)+(6+3+1)−0=10
例题:求从(0,0)点到(10,5)点得路径中不通过AB,CD,EF,GH的路径数,已知各点坐标为 A ( 2 , 2 ) , B ( 3 , 2 ) , C ( 4 , 2 ) , D ( 5 , 2 ) , E ( 6 , 2 ) , F ( 6 , 3 ) , G ( 7 , 2 ) , H ( 7 , 3 ) A(2,2),B(3,2),C(4,2),D(5,2),E(6,2),F(6,3),G(7,2),H(7,3) A(2,2),B(3,2),C(4,2),D(5,2),E(6,2),F(6,3),G(7,2),H(7,3)。
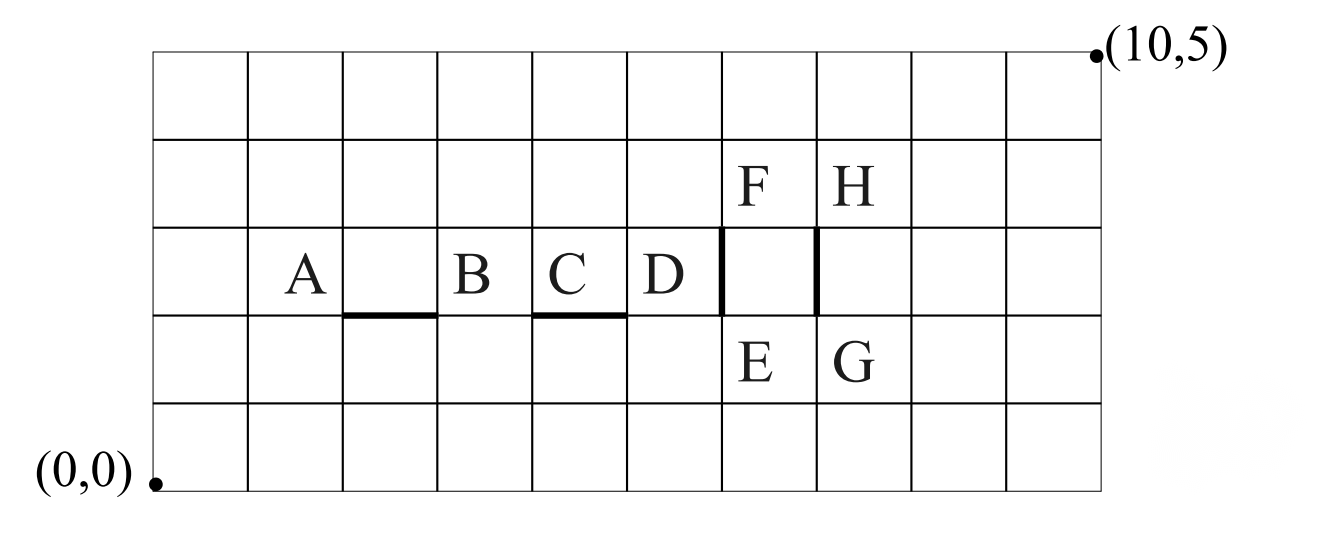
解:从(0,0)点到(10,5)点的所有路径数为 C 10 + 5 5 = 3003 C_{10+5}^{5}=3003 C10+55=3003(第一章的简单格路问题)
设 A 1 A_1 A1表示从(0,0)到(10,5)其中过AB的路径,
设 A 2 A_2 A2表示从(0,0)到(10,5)其中过CD的路径,
设 A 3 A_3 A3表示从(0,0)到(10,5)其中过EF的路径,
设 A 4 A_4 A4表示从(0,0)到(10,5)其中过GH的路径,
因此有
∣ A 1 ∣ = ( 4 2 ) ( ( 10 − 3 ) + ( 5 − 2 ) 5 − 2 ) = ( 4 2 ) ( 10 3 ) = 6 × 120 = 720 |A_1| =(\begin{array}{c} 4 \\ 2 \end{array}) (\begin{array}{c}(10-3)+(5-2) \\ 5-2 \end{array}) =(\begin{array}{l} 4 \\ 2\end{array}) (\begin{array}{l} 10 \\ 3 \end{array}) =6 \times 120 =720 ∣A1∣=(42)((10−3)+(5−2)5−2)=(42)(103)=6×120=720
同理
∣ A 2 ∣ = ( 6 2 ) ( 8 3 ) = 15 × 56 = 840 |A_2| =(\begin{array}{l} 6 \\ 2\end{array}) (\begin{array}{l} 8 \\ 3 \end{array}) =15 \times 56 =840 ∣A2∣=(62)(83)=15×56=840
∣ A 3 ∣ = ( 8 2 ) ( 6 2 ) = 28 × 15 = 420 |A_3| =(\begin{array}{l} 8 \\ 2\end{array}) (\begin{array}{l} 6 \\ 2 \end{array}) =28 \times 15 =420 ∣A3∣=(82)(62)=28×15=420
∣ A 4 ∣ = ( 9 2 ) ( 5 2 ) = 36 × 10 = 360 |A_4| =(\begin{array}{l} 9 \\ 2\end{array}) (\begin{array}{l} 5 \\ 2 \end{array}) =36 \times 10 =360 ∣A4∣=(92)(52)=36×10=360
∣ A 1 ∩ A 2 ∣ = ( 4 2 ) ( 8 2 ) = 6 × 56 = 336 |A_1 \cap A_2| =(\begin{array}{l} 4 \\ 2\end{array}) (\begin{array}{l} 8 \\ 2 \end{array}) =6 \times 56 =336 ∣A1∩A2∣=(42)(82)=6×56=336
∣ A 1 ∩ A 3 ∣ = ( 4 2 ) ( 6 2 ) = 6 × 15 = 90 |A_1 \cap A_3| =(\begin{array}{l} 4 \\ 2\end{array}) (\begin{array}{l} 6 \\ 2 \end{array}) =6 \times 15 =90 ∣A1∩A3∣=(42)(62)=6×15=90
∣ A 1 ∩ A 4 ∣ = ( 4 2 ) ( 5 2 ) = 6 × 10 = 60 |A_1 \cap A_4| =(\begin{array}{l} 4 \\ 2\end{array}) (\begin{array}{l} 5 \\ 2 \end{array}) =6 \times 10 =60 ∣A1∩A4∣=(42)(52)=6×10=60
∣ A 2 ∩ A 3 ∣ = ( 6 2 ) ( 6 2 ) = 15 × 15 = 225 |A_2 \cap A_3| =(\begin{array}{l} 6 \\ 2\end{array}) (\begin{array}{l} 6 \\ 2 \end{array}) =15 \times 15 =225 ∣A2∩A3∣=(62)(62)=15×15=225
∣ A 2 ∩ A 4 ∣ = ( 6 2 ) ( 5 2 ) = 15 × 10 = 150 |A_2 \cap A_4| =(\begin{array}{l} 6 \\ 2\end{array}) (\begin{array}{l} 5 \\ 2 \end{array}) =15 \times 10 =150 ∣A2∩A4∣=(62)(52)=15×10=150
∣ A 3 ∩ A 4 ∣ = 0 |A_3 \cap A_4|=0 ∣A3∩A4∣=0
∣ A 1 ∩ A 2 ∩ A 3 ∣ = ( 4 2 ) ( 6 2 ) = 6 × 15 = 90 |A_1 \cap A_2 \cap A_3| =(\begin{array}{l} 4 \\ 2\end{array}) (\begin{array}{l} 6 \\ 2 \end{array}) =6 \times 15 =90 ∣A1∩A2∩A3∣=(42)(62)=6×15=90
∣ A 1 ∩ A 2 ∩ A 4 ∣ = ( 4 2 ) ( 5 2 ) = 6 × 10 = 60 |A_1 \cap A_2 \cap A_4| =(\begin{array}{l} 4 \\ 2\end{array}) (\begin{array}{l} 5 \\ 2 \end{array}) =6 \times 10 =60 ∣A1∩A2∩A4∣=(42)(52)=6×10=60
∣ A 2 ∩ A 3 ∩ A 4 ∣ = 0 |A_2 \cap A_3 \cap A_4|=0 ∣A2∩A3∩A4∣=0
∣ A 1 ∩ A 2 ∩ A 3 ∩ A 4 ∣ = 0 |A_1 \cap A_2 \cap A_3 \cap A_4|=0 ∣A1∩A2∩A3∩A4∣=0
所以
∣ A 1 ‾ ∩ A 2 ‾ ∩ A 3 ‾ ∩ A 4 ‾ ∣ = 3003 − ( 720 + 840 + 420 + 360 ) + ( 336 + 90 + 60 + 225 + 150 ) − ( 90 + 60 ) = 3003 − 2340 + 861 − 150 = 1374 |\overline{A_1} \cap \overline{A_2} \cap \overline{A_3} \cap \overline{A_4}|=3003-(720+840+420+360)+(336+90+60+225+150)-(90+60)=3003-2340+861-150=1374 ∣A1∩A2∩A3∩A4∣=3003−(720+840+420+360)+(336+90+60+225+150)−(90+60)=3003−2340+861−150=1374
3.5 n对夫妻问题
例题: n n n对夫妻围圆桌而坐,每个男人都不和他的妻子相邻,有多少种方案?
解: n n n对夫妻有 2 n 2n 2n个人, 2 n 2n 2n个人围圆桌而坐的方案数为 ( 2 n − 1 ) ! (2n-1)! (2n−1)!
设 A i A_i Ai表示第 i i i对夫妻相邻而坐的集合, i = 1 , 2 , . . . , n i=1,2,...,n i=1,2,...,n,则问题转化为求
∣ A 1 ∩ A 2 ∩ … ∩ A n ∣ = N − ∑ i = 1 n ∣ A i ∣ + ∑ i = 1 n ∑ j > i ∣ A i ∩ A j ∣ − … + ( − 1 ) n ∣ A 1 ∩ A 2 ∩ … ∩ A n ∣ |A_1 \cap A_2 \cap \ldots \cap A_n| =N-\sum_{i=1}^n\left|A_i\right| +\sum_{i=1}^n \sum_{j>i}\left|A_i \cap A_j\right| -\ldots +(-1)^{n}\left|A_1 \cap A_2 \cap \ldots \cap A_n\right| ∣A1∩A2∩…∩An∣=N−i=1∑n∣Ai∣+i=1∑nj>i∑∣Ai∩Aj∣−…+(−1)n∣A1∩A2∩…∩An∣
∣ A i ∣ |A_i| ∣Ai∣相当于讲第 i i i对夫妻作为一个对象围圆桌,同一对夫妻之间可以换位,故
∣ A i ∣ = 2 Q 2 n − 1 2 n − 1 = 2 ( 2 n − 2 ) ! |A_i|=2Q_{2n-1}^{2n-1}=2(2n-2)! ∣Ai∣=2Q2n−12n−1=2(2n−2)!
∣ A i ∩ A j ∣ = 2 2 Q 2 n − 2 2 n − 2 = 2 2 ( 2 n − 3 ) ! |A_i \cap A_j|=2^2Q_{2n-2}^{2n-2}=2^2(2n-3)! ∣Ai∩Aj∣=22Q2n−22n−2=22(2n−3)!
∣ A i ∩ A j ∩ A k ∣ = 2 3 Q 2 n − 3 2 n − 3 = 2 2 ( 2 n − 4 ) ! |A_i \cap A_j \cap A_k|=2^3Q_{2n-3}^{2n-3}=2^2(2n-4)! ∣Ai∩Aj∩Ak∣=23Q2n−32n−3=22(2n−4)!
⋯ ⋯ \cdots \cdots ⋯⋯
∣ A 1 ∩ A 2 ∩ ⋯ A n ∣ = 2 n Q 2 n − n 2 n − n = 2 n ( n − 1 ) ! |A_1 \cap A_2 \cap \cdots A_n|=2^nQ_{2n-n}^{2n-n}=2^n(n-1)! ∣A1∩A2∩⋯An∣=2nQ2n−n2n−n=2n(n−1)!
故夫妻不相邻方案数为
M = ( 2 n − 1 ) ! − 2 ( n 1 ) ( 2 n − 2 ) ! + 2 2 ( n 2 ) ( 2 n − 3 ) ! − ⋯ + ( − 1 ) n 2 n ( n n ) ( n − 1 ) ! = ∑ h = 0 n ( − 1 ) h 2 h ( n h ) ( 2 n − h − 1 ) ! M=(2n-1)! -2(\begin{array}{l} n \\ 1 \end{array})(2n-2)! +2^2(\begin{array}{l} n \\ 2 \end{array})(2n-3)! -\cdots +(-1)^n 2^n(\begin{array}{l} n \\ n \end{array})(n-1)! \\ =\sum_{h=0}^n(-1)^h 2^h\left(\begin{array}{l} n \\ h \end{array}\right)(2n-h-1)! M=(2n−1)!−2(n1)(2n−2)!+22(n2)(2n−3)!−⋯+(−1)n2n(nn)(n−1)!=h=0∑n(−1)h2h(nh)(2n−h−1)!
例题: n n n对夫妻排成一列,每个男人都不和他的妻子相邻,有多少种可能的方案?
解:
M = ( 2 n ) ! − 2 ( n 1 ) ( 2 n − 1 ) ! + 2 2 ( n 2 ) ( 2 n − 2 ) ! − ⋯ + ( − 1 ) n 2 n ( n n ) ( n ) ! = ∑ h = 0 n ( − 1 ) h 2 h ( n h ) ( 2 n − h ) ! M=(2n)! -2(\begin{array}{l} n \\ 1 \end{array})(2n-1)! +2^2(\begin{array}{l} n \\ 2 \end{array})(2n-2)! -\cdots +(-1)^n 2^n(\begin{array}{l} n \\ n \end{array})(n)! \\ =\sum_{h=0}^n(-1)^h 2^h\left(\begin{array}{l} n \\ h \end{array}\right)(2n-h)! M=(2n)!−2(n1)(2n−1)!+22(n2)(2n−2)!−⋯+(−1)n2n(nn)(n)!=h=0∑n(−1)h2h(nh)(2n−h)!
3.6 错排问题
定义:一个排列其中所有的元素都不在原来的位置上,则称这个排列为错排,也叫重排。
证明: n n n个元素的错排为 n ! ( 1 − 1 1 ! + 1 2 ! − ⋯ ± 1 n ! ) n!(1-\frac{1}{1!}+\frac{1}{2!}-\cdots \pm \frac{1}{n!}) n!(1−1!1+2!1−⋯±n!1)
设 A i A_i Ai为数 i i i在第 i i i位上的全体排列, i = 1 , 2 , . . , n i=1,2,..,n i=1,2,..,n。因为数字 i i i不能动,因而有:
∣ A i ∣ = ( n − 1 ) ! , i = 1 , 2 , . . . , n |A_i|=(n-1)!,i=1,2,...,n ∣Ai∣=(n−1)!,i=1,2,...,n
∣ A i ∩ A j ∣ = ( n − 2 ) ! , i , j = 1 , 2 , . . , n , i ≠ j |A_i \cap A_j|=(n-2)!,i,j=1,2,..,n,i\neq j ∣Ai∩Aj∣=(n−2)!,i,j=1,2,..,n,i=j
⋯ ⋯ \cdots \cdots ⋯⋯
每个元素都不在原来位置的排列数为
∣ A 1 ‾ ∩ A 2 ‾ ∩ … ∩ A n ‾ ∣ = n ! − C ( n , 1 ) ( n − 1 ) ! + C ( n , 2 ) ( n − 2 ) ! − ⋯ − ± C ( n , n ) 1 ! = n ! ( 1 − 1 1 ! + 1 2 ! − ⋯ ± 1 n ! ) |\overline{A_1} \cap \overline{A_2} \cap \ldots \cap \overline{A_n}| =n! -C(n,1)(n-1)! +C(n, 2)(n-2)! -\cdots -\pm C(n,n)1! \\ =n!(1-\frac{1}{1!}+\frac{1}{2!}-\cdots \pm \frac{1}{n!}) ∣A1∩A2∩…∩An∣=n!−C(n,1)(n−1)!+C(n,2)(n−2)!−⋯−±C(n,n)1!=n!(1−1!1+2!1−⋯±n!1)
例题:1,2,…,9的全排列中,求偶数都在原来的位置上,其余都不在原来位置上的错排数目。
解:实际上是1,3,5,7,9五个数的错排问题,总数为:
5 ! − C ( 5 , 1 ) 4 ! + C ( 5 , 2 ) 3 ! − C ( 5 , 3 ) 2 ! + C ( 5 , 4 ) 1 ! − C ( 5 , 5 ) = 120 ( 1 2 − 1 6 + 1 24 − 1 120 ) = 44 5!-C(5,1)4!+C(5,2)3!-C(5,3)2!+C(5,4)1!-C(5,5) =120(\frac{1}{2}-\frac{1}{6}+\frac{1}{24}-\frac{1}{120}) =44 5!−C(5,1)4!+C(5,2)3!−C(5,3)2!+C(5,4)1!−C(5,5)=120(21−61+241−1201)=44
3.7 棋盘多项式和有禁区的排列
对于 X = 1 , 2 , . . . , n X={1,2,...,n} X=1,2,...,n的一个排列恰好对应了 n n n个棋子在 n × n n \times n n×n棋盘上的一种布棋方案。以棋盘的行表示 X X X中的元素element,列表示排列中的位置position。如下图所示这种放棋方案就对应了排列2143。
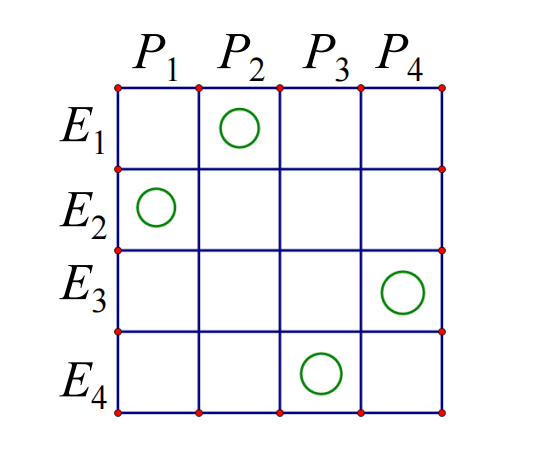
如果在排列种限制元素 i i i不能排列在第 j j j个位置,则相应的布棋方案种的第 i i i行第 j j j列的方格不允许放棋子。把所有这些不许放棋的方格称为禁区。
对于 { 1 , 2 , 3 , 4 } \{1,2,3,4\} {1,2,3,4}的一个排列 P = e 1 e 2 e 3 e 4 P=e_1e_2e_3e_4 P=e1e2e3e4,规定 e 1 ≠ 3 , e 2 ≠ 1 , 4 , e 3 ≠ 2 , 4 , e 4 ≠ 2 e_1\neq3,e_2\neq1,4,e_3 \neq2,4,e_4 \neq2 e1=3,e2=1,4,e3=2,4,e4=2。这样的排列对应于有禁区的布子。如下图有阴影的格子表示禁区。
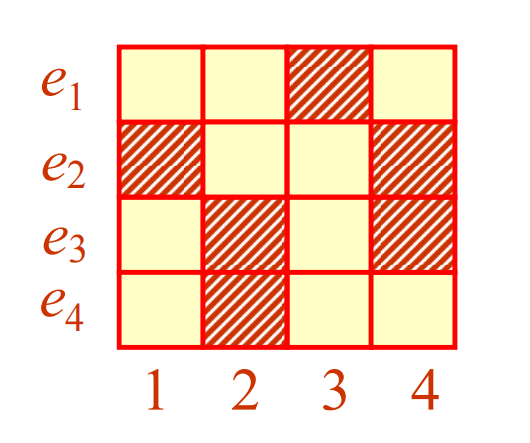
棋盘多项式:设 C C C为一棋盘,称 ∑ k = 0 n r k ( C ) x k \sum_{k=0}^{n} r_k(C)x^k ∑k=0nrk(C)xk为 C C C的棋盘多项式,其中 r k ( C ) r_k(C) rk(C)表示 k k k个棋子布到棋盘 C C C的方案数。规定 r 0 ( C ) = 1 r_0(C)=1 r0(C)=1。
性质:
- 设 C i C_i Ci是棋盘 C C C的某一指定格子所在的行与列都去掉后所得的棋盘, C e C_e Ce是仅去掉该格子后的棋盘,则 r k ( C ) = r k − 1 ( C i ) + r k ( C e ) r_k(C)=r_{k-1}(C_i)+r_k(C_e) rk(C)=rk−1(Ci)+rk(Ce)。
- 如果 C C C由互相分离的 C 1 C_1 C1和 C 2 C_2 C2组成,即 C 1 C_1 C1的任一格子所在的行和列中都没有 C 2 C_2 C2的格子,则有 r k ( C ) = ∑ i = 0 k r i ( C 1 ) r k − i ( C 2 ) r_k(C)=\sum_{i=0}^{k}r_i(C_1)r_{k-i}(C_2) rk(C)=∑i=0kri(C1)rk−i(C2)。
定理:设 r i r_i ri为 i i i个棋子布入禁区的方案数, i = 1 , 2 , 3 , . . . n i=1,2,3,...n i=1,2,3,...n。有禁区的布子方案数(即禁区内不布子的方案数)为,
r 0 n ! − r 1 ( n − 1 ) ! + r 2 ( n − 2 ) ! − ⋯ + ( − 1 ) n r n = ∑ k = 0 n ( − 1 ) k r k ( n − k ) ! r_0n!-r_1(n-1)!+r_2(n-2)!-\cdots+(-1)^n r_n = \sum_{k=0}^{n} (-1)^{k} r_{k}(n-k)! r0n!−r1(n−1)!+r2(n−2)!−⋯+(−1)nrn=k=0∑n(−1)krk(n−k)!
定理证明见棋盘多项式 - 维基百科,自由的百科全书 (wikipedia.org)
例题:如下所示,在 4 × 4 4\times4 4×4的棋盘上,打叉的地方为禁区,求棋子无一落入禁区的排列数。
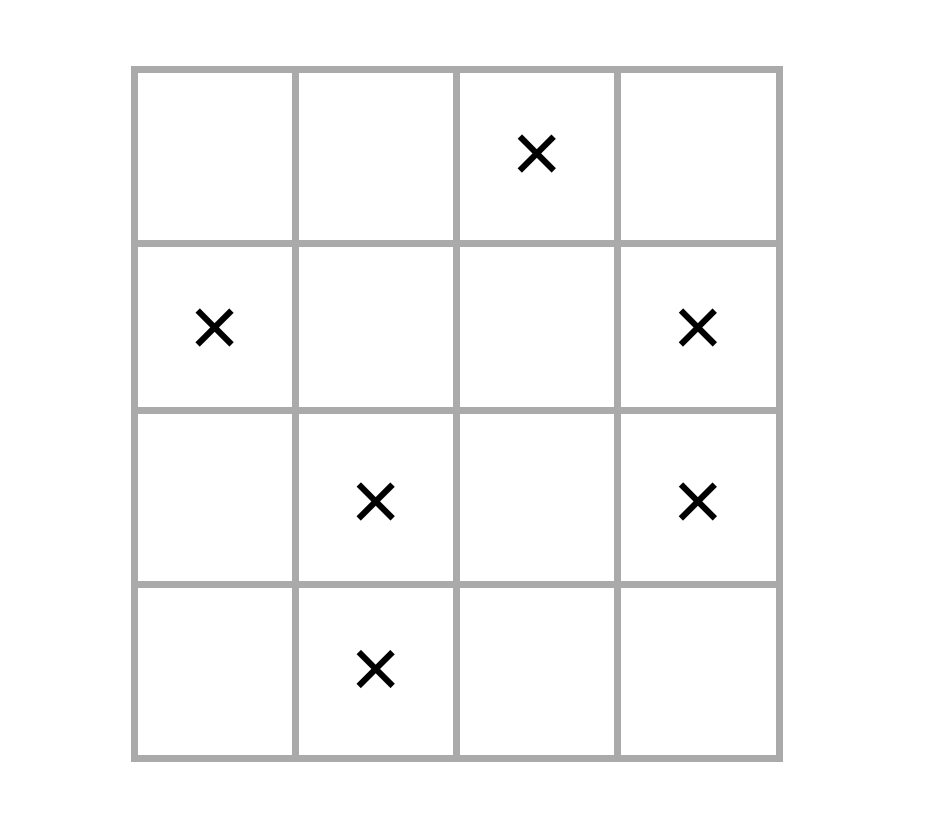
解:首先计算棋盘多项式,即 r 0 ( C ) + r 1 ( C ) x + r 2 ( C ) x 2 + r 3 ( C ) x 3 + r 4 ( C ) x 4 r_0(C)+r_1(C)x+r_2(C)x^2+r_3(C)x^3+r_4(C)x^4 r0(C)+r1(C)x+r2(C)x2+r3(C)x3+r4(C)x4,只需依次计算 r 0 , r 2 , r 2 , r 3 , r 4 r_0,r_2,r_2,r_3,r_4 r0,r2,r2,r3,r4即可。
由规定知 r 0 ( C ) = 1 r_0(C)=1 r0(C)=1,
r 1 ( C ) r_1(C) r1(C)即1个棋子布到棋盘 C C C的方案数,棋盘 C C C有6个禁区,这一个棋子可以布到这6个地方且不存在其他棋子与这一个棋子冲突,因此 r 1 ( C ) = 6 r_1(C)=6 r1(C)=6;
r 2 ( C ) r_2(C) r2(C)即2个棋子布到棋盘 C C C的方案数,从6个禁区中找到两个不在同一行不在同一列的。有(1,3)和(2,1),(1,3)和(2,4),(1,3)和(3,2),(1,3)和(3,4),(1,3)和(4,2),(2,1)和(3,2),(2,1)和(3,4),(2,1)和(4,2),(2,4)和(3,2),(2,4)和(4,2),(3,4)和(4,2),共11种。即 r 2 r_2 r2©=11;
r 3 ( C ) r_3(C) r3(C)即3个棋子布到棋盘 C C C的方案数,得到 r 3 ( C ) = 7 r_3(C)=7 r3(C)=7;
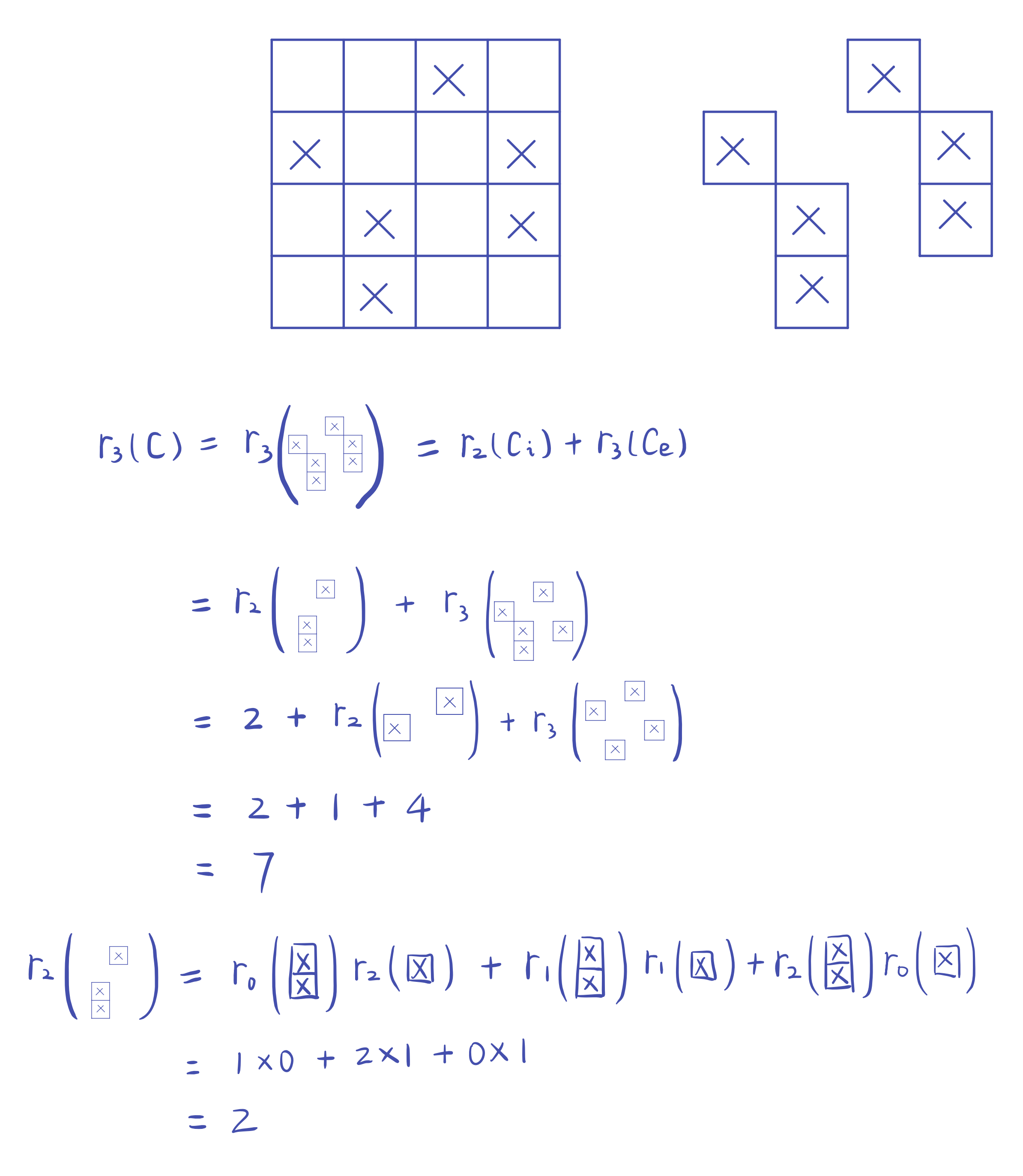
r 4 ( C ) r_4(C) r4(C)即4个棋子布到棋盘 C C C的方案数,四个棋子要求都不同行不同列,只有一种方案,即 r 4 ( C ) = 1 r_4(C)=1 r4(C)=1;
综上得棋盘多项式为 1 + 6 x + 11 x 2 + 7 x 3 + x 4 1+6x+11x^2+7x^3+x^4 1+6x+11x2+7x3+x4,再结合定理得无一落入禁区得排列数为 1 × 4 ! − 6 × ( 4 − 1 ) ! + 11 × ( 4 − 2 ) ! − 7 × ( 4 − 3 ) ! + 1 × ( 4 − 4 ) ! = 24 − 36 + 22 − 7 + 1 = 4 1\times4!-6\times(4-1)!+11\times(4-2)!-7\times(4-3)!+1\times(4-4)! = 24-36+22-7+1=4 1×4!−6×(4−1)!+11×(4−2)!−7×(4−3)!+1×(4−4)!=24−36+22−7+1=4。
3.8 有限制的排列
-
有禁区排列是对元素排列位置的限制,计算的是绝对禁用位置;
-
有限制排列讲的是相对禁用位置,它限制的是对元素之间的相邻关系的限制 。也称为有限制条件(模式)的排列
-
这里谈的有限制排列与前面章节提到的“受限多重排列”不同。
3.9 鸽巢原理
鸽巢原理是组合数学中最简单也是最基本的原理,也叫抽屉原理。
-
若有n个鸽子巢,n+1个鸽子,则至少有一个巢内有至少有两个鸽子。
-
m m m只各自, n n n个鸽巢,至少有一个鸽巢里有不少于 ⌊ m − 1 n ⌋ + 1 \lfloor\frac{m-1}{n}\rfloor+1 ⌊nm−1⌋+1只鸽子。
-
m 1 , m 2 , . . . , m n m_1,m_2,...,m_n m1,m2,...,mn都是正整数,并有 m 1 + m 2 + ⋯ + m n − n + 1 m_1+m_2+\cdots+m_n-n+1 m1+m2+⋯+mn−n+1个鸽子住进 n n n个鸽巢,则至少对某个 i i i有第 i i i个巢中至少有 m i m_i mi个鸽子, i = 1 , 2 , . . . , n i=1,2,...,n i=1,2,...,n。
-
设 k k k和 n n n都是任意正整数,若至少有 k n + 1 kn+1 kn+1只鸽子分配在 n n n个鸽巢,则至少有一个鸽巢里有至少 k + 1 k+1 k+1只鸽子。
-
若取 n ( m − 1 ) + 1 n(m-1)+1 n(m−1)+1个球放进 n n n个盒子,则至少有一个盒子有 m m m个球。
-
若 m 1 , m 2 , . . . , m n m_1,m_2,...,m_n m1,m2,...,mn是正整数,且 m 1 + m 2 + . . . + m n n > r − 1 \frac{m_1+m_2+...+m_n}{n} \gt {r-1} nm1+m2+...+mn>r−1,则 m 1 , m 2 , . . . , m n m_1,m_2,...,m_n m1,m2,...,mn中至少有一个数不小于 r r r。
3.9.1 整除问题
例题:如果有 n + 1 n+1 n+1个正整数,而这些整数是小于或等于 2 n 2n 2n,是否一定会有一对数是互素的?为什么?
解:证明,如果从 { 1 , 2 , . . . , 2 n } \{1,2,...,2n\} {1,2,...,2n}中选择 n + 1 n+1 n+1个整数,那么存在两个整数,它们之间差为1。
设选择的 n + 1 n+1 n+1个整数为 a 1 , a 2 , . . . , a n + 1 , a 1 < a 2 < . . . < a n a_1,a_2,...,a_{n+1},a_1 \lt a_2 \lt ... \lt a_n a1,a2,...,an+1,a1<a2<...<an,令 b 1 = a 1 + 1 , b 2 = a 2 + 1 , . . . , b n = a n + 1 b_1=a_1+1,b_2=a_2+1,...,b_n=a_n+1 b1=a1+1,b2=a2+1,...,bn=an+1,
则 1 < b 1 < b 2 < . . . < b n ≤ 2 n 1 \lt b_1 \lt b_2 \lt ... \lt b_n \le 2n 1<b1<b2<...<bn≤2n。
a 1 , a 2 , . . . , a n + 1 , b 1 , b 2 , . . . , b n a_1,a_2,...,a_{n+1},b_1,b_2,...,b_n a1,a2,...,an+1,b1,b2,...,bn这 2 n + 1 2n+1 2n+1个数,但范围只有 2 n 2n 2n,所以其中至少有一对相等,且 b j = a j + 1 b_j=a_j+1 bj=aj+1, b j = a k b_j=a_k bj=ak所有 a k a_k ak和 a j a_j aj只相差1。因此得证。
3.9.2 图形问题
例题:在边长为1的等边三角形内任意选择5个点,存在两个点,其间距最多为 1 2 \frac{1}{2} 21。在边长为1的等边三角形内任意选择10个点,存在两个点,其间距最多为 1 3 \frac{1}{3} 31.
解:
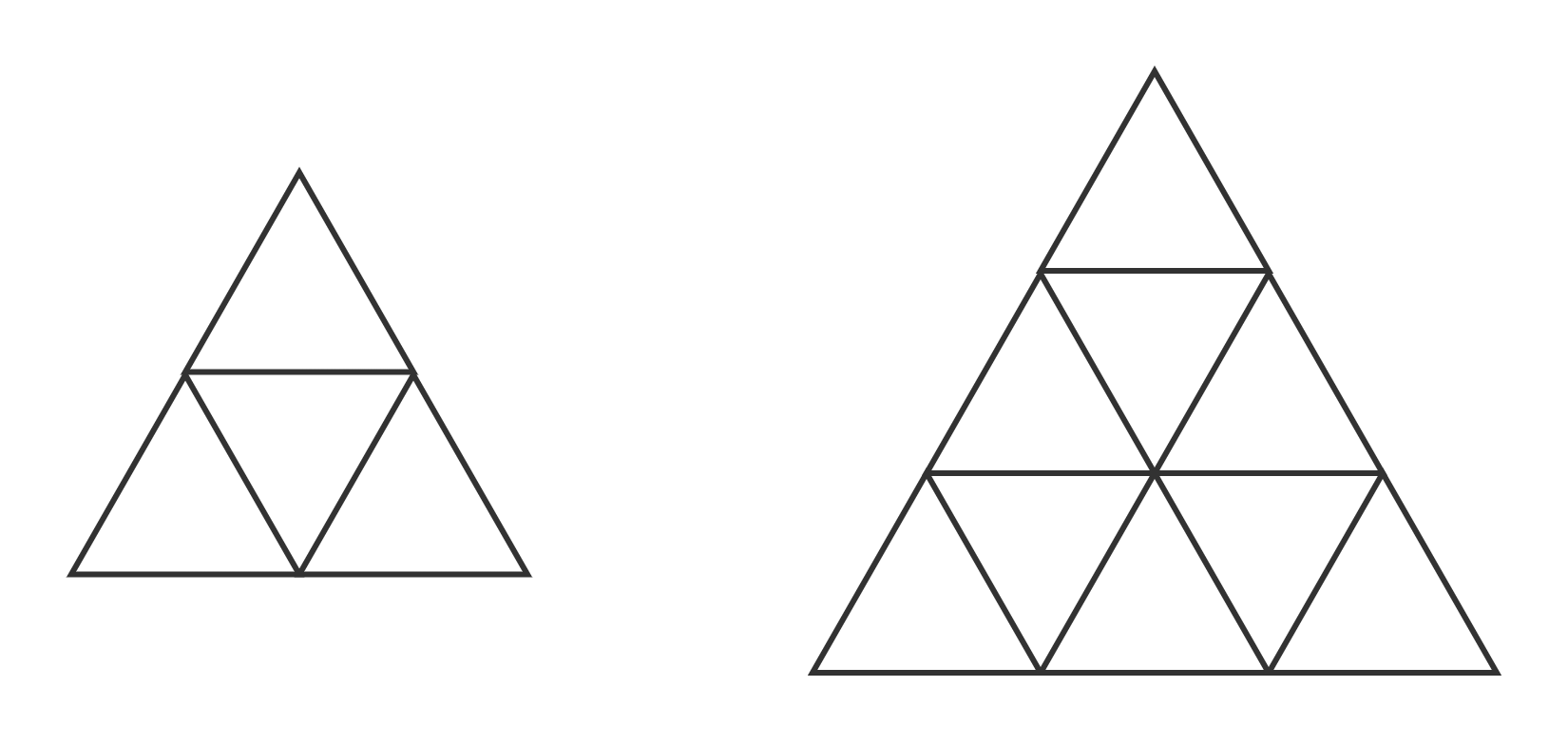
有4个小三角形,任选5个点,必有两个点在同一小三角形内。/有9个小三角形,任选10个点必有两个点在同一小三角形内。鸽巢原理。
3.9.3 连续累加问题
例题:设 a 1 , a 2 , . . . a m a_1,a_2,...a_m a1,a2,...am是正整数序列,则至少存在 k k k和 l l l, 1 ≤ k < l ≤ m 1\le k \lt l \le m 1≤k<l≤m,使得和 a k + a k + 1 + ⋯ + a l a_k+a_{k+1}+\cdots+a_l ak+ak+1+⋯+al是 m m m的倍数。
证明:设 S h = ∑ i = 1 h a i S_h=\sum_{i=1}^{h}a_i Sh=∑i=1hai, S h ≡ r h m o d m , 0 ≤ r h ≤ m − 1 , h = 1 , 2 , . . . , m S_h\equiv r_h mod m,0 \le r_h \le m-1,h=1,2,...,m Sh≡rhmodm,0≤rh≤m−1,h=1,2,...,m。若存在 l l l, S l ≡ 0 m o d m S_l \equiv 0modm Sl≡0modm,则命题成立。否则, 1 ≤ r h ≤ m − 1 1 \le r_h \le m-1 1≤rh≤m−1,但 h = 1 , 2 , . . . , m h=1,2,...,m h=1,2,...,m,由鸽巢原理知,存在 r k = r h r_k=r_h rk=rh,即 S k ≡ S h m o d m S_k\equiv S_hmodm Sk≡Shmodm,不妨设 h > k h \gt k h>k,则 S h − S k = a k + 1 + a k + 2 + ⋯ + a h ≡ 0 m o d m S_h-S_k=a_{k+1}+a_{k+2}+\cdots+a_h \equiv 0modm Sh−Sk=ak+1+ak+2+⋯+ah≡0modm。
例题:一个孩子每天至少做一题,总共做7周,每周总共不超过11题。必存在连续若干天在次期间这个孩子恰好做了20题。
证明:设 a 1 , a 2 , . . . a 49 a_1,a_2,...a_{49} a1,a2,...a49, S k = a 1 + a 2 + ⋯ + a k S_k=a_1+a_2+\cdots+a_k Sk=a1+a2+⋯+ak,即证必定存在 0 ≤ k < l ≤ 49 , a k + 1 + a k + 2 + ⋯ + a l = 20 0 \le k \lt l \le49,a_{k+1}+a_{k+2}+\cdots+a_l=20 0≤k<l≤49,ak+1+ak+2+⋯+al=20,即 S l − S k = 20 S_{l}-S_k=20 Sl−Sk=20。
其中 1 ≤ S 1 , S 2 , . . . S 49 ≤ 77 1 \le S_1,S_2,...S_{49} \le 77 1≤S1,S2,...S49≤77,构造 b 1 = S 1 + 20 , . . . , b 49 = S 49 + 20 ≤ 97 b_1=S_1+20,...,b_{49}=S_{49}+20 \le 97 b1=S1+20,...,b49=S49+20≤97。
1 ≤ S 1 , S 2 , . . . , S 49 , b 1 , b 2 , . . . b 49 ≤ 97 1 \le S_1,S_2,...,S_{49},b_1,b_2,...b_{49} \le 97 1≤S1,S2,...,S49,b1,b2,...b49≤97,98个元素,但最高只能取到97,根据鸽巢原理其中必有两个元素相等。即存在 b k = S l b_k=S_l bk=Sl,而 b k = S k + 20 b_k=S_k+20 bk=Sk+20,所以 S k + 20 = S l S_k+20=S_l Sk+20=Sl,即 S l − S k = 20 S_l-S_k=20 Sl−Sk=20。
类似问题:生产产品、看电视、做运动…
例题:设 a 1 , a 2 , . . . a 100 a_1,a_2,...a_{100} a1,a2,...a100是由1和2组成的序列,已知从其任一数开始的顺序10个数的和不超过16,即 a i + a i + 1 + ⋯ + a i + 9 ≤ 16 , 1 ≤ i ≤ 91 a_i+a_{i+1}+\cdots+a_{i+9} \le16,1\le i \le 91 ai+ai+1+⋯+ai+9≤16,1≤i≤91,则至少存在 h h h和 k k k, k > h k \gt h k>h,使得 a h + a h + 1 + ⋯ + a k = 39 a_h+a_{h+1}+\cdots+a_k=39 ah+ah+1+⋯+ak=39。
证明:令 S j = ∑ i = 1 j a i , j = 1 , 2 , . . . , 100 S_j=\sum_{i=1}^{j}a_i,j=1,2,...,100 Sj=∑i=1jai,j=1,2,...,100,显然 S 1 < S 2 < ⋯ < S 100 S_1 \lt S_2 \lt \cdots \lt S_{100} S1<S2<⋯<S100,且 S 100 ≤ 10 × 16 = 160 S_{100} \le 10 \times 16=160 S100≤10×16=160
做序列 S 1 , S 2 , . . . , S 100 , S 1 + 39 , . . . S 100 + 39 S_1,S_2,...,S_{100},S_1+39,...S_{100}+39 S1,S2,...,S100,S1+39,...S100+39共200项。其中最大项 S 100 + 39 ≤ 160 + 39 = 199 S_{100}+39 \le 160+39=199 S100+39≤160+39=199。
由鸽巢原理,必有两项相等,而且必是前段中的某项与后段中的某项相等,设 S k = S h + 39 , k > h , S k − S h = 39 S_k=S_h+39,k \gt h,S_k-S_h=39 Sk=Sh+39,k>h,Sk−Sh=39,即 a h + a h + 1 + ⋯ + a k = 39 a_h+a_{h+1}+\cdots+a_k=39 ah+ah+1+⋯+ak=39
这篇关于组合数学_第3章_容斥原理与鸽巢原理的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





