数据结构--排序算法(冒泡排序快速排序鸽巢排序)

本文主要是介绍数据结构--排序算法(冒泡排序快速排序鸽巢排序)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

插入排序以及选择排序请查阅我往期博客：http://blog.csdn.net/sayhello_world/article/details/61927082

冒泡排序：

思想：两两交换，大的放到后面。重复size-1次

代码实现：

[cpp]  view plain copy  
 //冒泡排序  
 void Bubble_Sort(int array[],int size)  
 {  
     for(int idx= 0; idx < size;++idx)  
     {  
        for(int index= 0; index < size-1-idx;++index)  
        {  
            if(array[index]> array[index+1])  
            {  
               std::swap(array[index],array[index+1]);  
            }  
        }  
     }  
 }  

冒泡排序的优化：

思想：对冒泡排序常见的改进方法是加入一标志性变量flag，用于标志某一趟排序过程中是否有数据交换，如果进行某一趟排序时并没有进行数据交换，则说明数据已经按要求排列好，可立即结束排序，避免不必要的比较过程。

代码实现：

[cpp]  view plain copy  
 //冒泡排序优化  
 void Bubble_Sort2(int array[], int size)  
 {  
     bool flag = true;  
     while (flag)  
     {  
         flag = false;  
         for (int index = 0; index < size - 1; ++index)  
         {  
             if (array[index] > array[index + 1])  
             {  
                 std::swap(array[index], array[index + 1]);  
                 flag = true;  
             }  
         }  
     }  
 }  

快速排序：

递归：

快速排序第一种方法：

思想：选取一个数字为比较值，用右值和他比较，如果右值比他小就将他给左边，左边加一。

若左边比他大，就将他给右边，右边减一。如此当left==right时，说明此比较值的地方就应该在此，然后递归，先排此地点的左边再排此地点的右边。

优化：可以写一个函数为查找最左边下标，最右边下标以及中间下标的中间值，在数组范围内比较数组下标第一个，最后一个，和中间值得元素，尽可能将值为中间的元素当成key值，这样可以提高效率。（因为递归时左和右都有将近一半的数据）

代码：

[cpp]  view plain copy  
 //三数取中法  
 int FindMidIndex(int array[],int left,int right)  
 {  
     int mid= right - ((right- left) >> 1);  
     if(array[left]<= array[mid])  
     {  
    
        if(array[right]< array[left])  
            return left;  
        if(array[right]> array[mid])  
            return mid;  
        else  
            return right;  
     }  
     if(array[left]> array[mid])  
     {  
        if(array[right]> array[mid])  
            return mid;  
        if(array[right]> array[left])  
            return left;  
        else  
            return right;  
     }  
     return 0;  
 }  
    

全过程

时间复杂度：O（NlogN）

空间复杂度：O（1）

稳定性：不稳定

代码实现：

[cpp]  view plain copy  
 int Quick_Pass1(int array[],int left,int right)  
 {  
     //设置一个比较的值尽量让比较值为较为中间的值  
     int keyIdx= FindMidIndex(array,left,right);  
     std::swap(array[keyIdx],array[right]);  
    
     int temp= array[right];  
    
     while(left < right)  
     {  
        //如果这时左边比比较值大左边给右边右边前移  
        while(left < right&& array[left]< temp)  
            left++;  
        if(left < right)  
        {  
            array[right]= array[left];  
            right--;  
        }  
    
        //如果右边比比较值小则右边的数值给左边，左边后移  
        while(left < right&& array[right]>= temp)  
            right--;  
        if(left < right)  
        {  
            array[left]= array[right];  
            left++;  
        }  
     }  
     //最后一个他俩相等的时候把中间比较值给过来返回中间的下标  
     array[left]= temp;  
     returnleft;  
 }  

快速排序第二种方法：

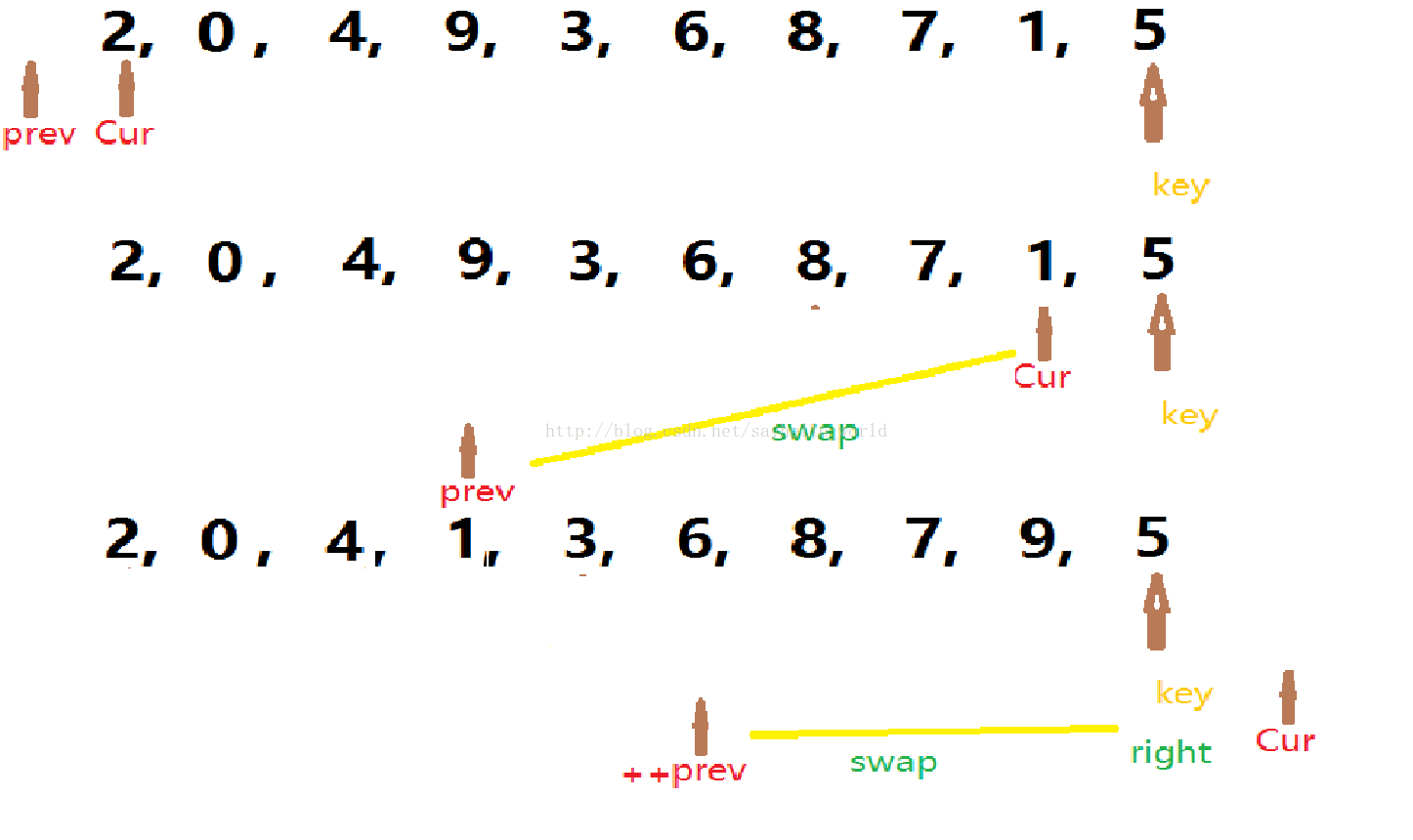
思路：给两个指针，第一个为Cur，第二个为prev，比较值为key，当Cur小于等于right时就一直循环。（这里如果没有等于就会少比较一次）当cur下标的元素小于比较值得时候，并且++prev！=cur ,就让array[cur]和array[prev]交换。当走完了之后，最后一个数据array[right]应该和array[++prev]交换，因为没有比较最后一个（cur下标的元素小于比较值，这里没有等于），也就少换了一个。

一趟之后：

代码实现：

[cpp]  view plain copy  
 //设置一个Pre与Cur 当Cur<=right的时候，就循环  
 //当遇到Cur<key且Pre下一个不为Cur时,就让array[Cur]与array[Pre]交换  
 //找小于key的数与大于key的数字交换  
 int Quick_Pass2(intarray[],intleft,intright)  
 {  
     int cur= left;  
     int prev= cur - 1;  
     int keyIdx= FindMidIndex(array,left,right);  
     std::swap(array[keyIdx],array[right]);  
     int key= array[right];  
    
     while(cur <= right)  
     {  
        //这里不用<=是因为防止重复数据若出现重复复数据会交换很多次  
        if(array[cur]< key && ++prev!= cur)  
            std::swap(array[cur],array[prev]);  
    
        ++cur;  
     }  
     std::swap(array[++prev],array[right]);  
     return prev;  
 }  

递归优化：

我们可知，当数据量较小的时候直接插入排序比较高效，所以当数据量较小的时候我们可以选择插入排序，当数据量较大的时候我们选择快速排序。

代码实现：

[cpp]  view plain copy  
 //递归快速排序  
 void Quick_Sort(intarray[],intleft,intright)  
 {  
     if(right - left<16)  
     {  
        Insert_Sort(array,right-left+1);  
     }  
    
     else  
     {  
        //先找到第一个数字应该放的点  
        intpos= Quick_Pass1(array,left,right);  
        //排这个数的左边的范围  
        Quick_Sort(array,left,pos-1);  
        //排这个数右边的范围  
        Quick_Sort(array, pos+ 1,right);  
     }  
 }  

快速排序非递归：

思路：递归转换为非递归一般用栈。我们向栈中保存数组下标，通过循环来进行排序。

代码实现：

[cpp]  view plain copy  
 //非递归快速排序  
 void Quick_Sort_Nor(intarray[],intleft,intright)  
 {  
     stack<int> s;  
     s.push(right);  
     s.push(left);  
    
     while(!s.empty())  
     {  
        left= s.top();  
        s.pop();  
        right= s.top();  
        s.pop();  
    
        intdiv= Quick_Pass2(array,left,right);  
        //此时可能会出现越界的问题如果最后一个就为最大值或者第一个就为最小值  
        if(div - 1 > left)  
        {  
            //因为上面是先读取左再读取右  所以这里为先压右再压左  
            s.push(div - 1);  
            s.push(left);  
        }  
    
        if(div + 1 < right)  
        {  
            s.push(right);  
            s.push(div + 1);  
        }  
     }  
 }  

鸽巢排序：

思路：如果遇见数据量大，数据杂乱度较高的一组数据。我们可以通过重新建立一个数组，此数组中存储数字出现的次数，下标加上最小的一个数字，此数字就为存入的数字。

最终只需要在新数组中存放存储数字即可。

时间复杂度：O（M+N）（M为存元素数目的区间，N为原数组区间）

空间复杂度：O（N）（N为区间大小）

实现代码：

[cpp]  view plain copy  
 //鸽巢排序  
 //思路:把数据存到一个数组里数组里存放次数据出现的次数  
 void Count_Sort(intarray[],intsize)  
 {  
     int maxValue= array[0];  
     int minValue= array[0];  
    
     for(int idx= 0; idx < size;++idx)  
     {  
        if(array[idx]> maxValue)  
            maxValue= array[idx];  
        if(array[idx]< minValue)  
            minValue= array[idx];  
     }  
    
     int range= maxValue - minValue+ 1;  
     int* count = newint[range];  
     memset(count, 0, sizeof(int)*range);  
    
     for(int idx= 0; idx < size;++idx)  
     {  
        count[array[idx]]++;  
     }  
    
     size_t index = 0;  
     for(int i= 0; i < range;++i)  
     {  
        for(int j= 0; j < count[i];++j)  
        {  
            array[index++]= minValue+i;  
        }  
     }  
    
     delete[]count;  
 }  