锥体专题
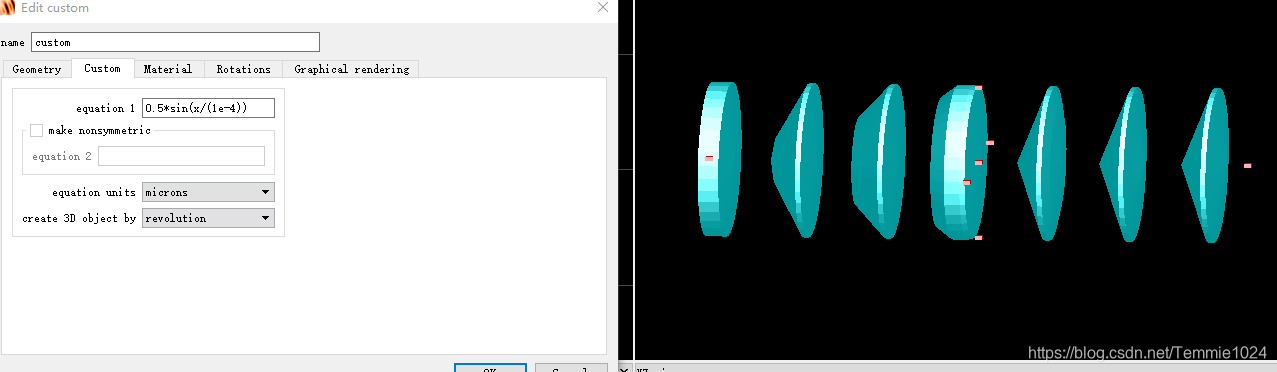
在FDTD中创建锥体
居然没有锥体这个基础几何体!再不济圆柱加一个末端半径缩成锥不行吗?然而并没有。 去官网找了一下,看到了一个类似的。是使用自定义形状在结构组中创建的。 官网给出的创建原代码(不是锥体,是一个圆台掏空内部。) 用户属性 结构组的脚本 deleteall;############################################### Truncated Cone# A tap
threejs 根据camera创建Frustum视锥体对象
版本 0.159.0 解决 // 如有需要更新相机的对象矩阵和投影矩阵camera.updateMatrix();camera.updateMatrixWorld();camera.updateProjectionMatrix();// 创建视锥体对象var frustum = new THREE.Frustum().setFromProjectionMatrix(new THRE
【Overload游戏引擎细节分析】从视图投影矩阵提取视锥体及overload对视锥体的封装
overoad代码中包含一段有意思的代码,可以从视图投影矩阵逆推出摄像机的视锥体,本文来分析一下原理 一、平面的方程 视锥体是用平面来表示的,所以先看看平面的数学表达。 平面方程可以由其法线N=(A, B, C)和一个点Q=(x0,y0,z0)定义,其形式为: A ( x − x 0 ) + B ( y − y 0 ) + C ( z − z 0 ) = 0 A(x-x_{0})+B(
【Overload游戏引擎分析】从视图投影矩阵提取视锥体及overload对视锥体的封装
overoad代码中包含一段有意思的代码,可以从视图投影矩阵逆推出摄像机的视锥体,本文来分析一下原理 一、平面的方程 视锥体是用平面来表示的,所以先看看平面的数学表达。 平面方程可以由其法线N=(A, B, C)和一个点Q=(x0,y0,z0)定义,其形式为: A ( x − x 0 ) + B ( y − y 0 ) + C ( z − z 0 ) = 0 A(x-x_{0})+B(