电磁场专题
Ansys的电磁场分析和系统电路仿真软件Electronics 2024 R1版本在Windows系统的下载与安装配置
目录 前言一、许可管理工具安装二、许可配置三、EM安装四、MCAD和帮助文件安装(可选择,非必要)总结 前言 “ ANSYS Electromagnetics Suite或ANSYS Electronics Suite是几个功能强大的程序的集合,用于仿真系统的电磁。ANSYS电磁套件还公开了行业分支机构和专业目录,并有标志。例如,在设备中,机电,如发动机、发电机等成为一员,继
热电子光探测器的电磁场空间分布与FDTD材料折射率的导出
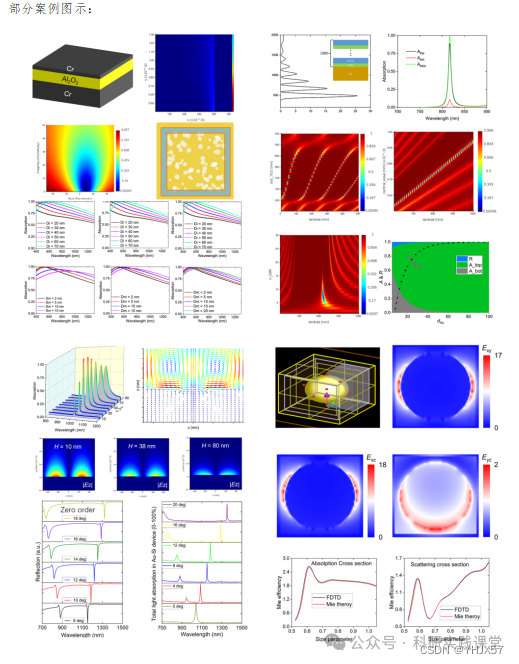
仿真实例 Ø 金属薄膜中金纳米孔阵列透射与反射, 并考虑其近场电磁分布 Ø 利用脚本进行电磁场及其光学响应的可视化 Ø 设置EOT型超表面结构,以及Structure library的使用 Ø 结构的参数化扫描与结果可视化 Ø 利用脚本计算峰值增强因子 Ø 多层平面结构激发Tamm等离激元诱导强光学吸收 Ø 金属小球Mie散射模型构建及脚本远场近场结果可视化 Ø 利用脚本计算热载
【模电】电场、磁场、电磁场的屏蔽原理
简述电场、磁场、电磁场的屏蔽原理及屏蔽要点:https://wenku.baidu.com/view/2f4a7622b84ae45c3b358cae.html 电磁屏蔽技术:https://wenku.baidu.com/view/d4549f3a294ac850ad02de80d4d8d15abf23007f.html 电磁场屏蔽的机理:https://wenku.baidu.com/vi
基于Matlab的电磁场与波“电轴法”仿真
0、代码中用到的drawEline函数 在使用代码前记得把这个函数和仿真文件放到一个文件夹下哦 function pipi=drawEline(h1,d1,d2)posAxes = get(gca, 'Position'); %获取当前坐标区位置信息posX = posAxes(1);posY = posAxes(2);width = posAxes(3);height = posA
【你也能看得懂的电磁场与电磁波系列连载 20】
在上一篇连载里面,我们证明了为什么: 同时也得到了 M a x w e l l Maxwell Maxwell 方程中描述电场和磁场公式的微分形式: 那么在今天的连载里面,我们重点想看看闭合曲线的线积分应该如何变成微分形式。 我们回顾一下我们对闭合曲面的面积分的微分处理——我们让闭合曲面 S 不断缩小,那么意味着闭合曲面 S 所包围的体积也是不断趋于0. 然后我们再同时除以闭合曲面
电动力学专题:电磁场规范不变性与规范自由度
对称性,不变性,相对性,协变形 在现代物理学中常常被认为具有相同的含义(好拗口) 规范与规范的自由度 保证电磁场物理量不改变的情况下,有多组势可供选择,而每组势可以称为一个规范 规范不变性:当势做规范变换时,所有物理量和物理规律都保持不变规范不变性是决定相互作用形式的一条基本原理,传递这些相互作用的场称作规范场 对于电磁场而言,我们由麦克斯韦方程组导出的的电场与磁场的旋度而没有规定其
用麦克斯韦方程组分析静电场,恒定电场,恒定磁场,磁准稳态场,电准稳态场,时变电磁场
用麦克斯韦方程组分析静电场,恒定电场,恒定磁场,磁准稳态场,电准稳态场,时变电磁场 麦克斯韦方程组深刻揭示了电磁场中的电场和磁场的空间分布及随时间变化的规律,本文给出了麦克斯韦方程组在静电场、恒定电场、恒定磁场、磁准稳态场、电准稳态场中的表现形式。 麦克斯韦方程组描述时变电磁场 麦克斯韦方程组的微分形式如公式(1)、(2)、(3)、(4)所示: ∇ × H ⃗ = ∂ D ⃗ ∂ t +
《电磁场与电磁波》(谢处方第5版)anki卡片学习笔记txt文件输出
#separator:tab #html:true #tags column:9 矢量叉乘A×B= (用 A、 B的模表示具体的值) e nABsinθ 其中 e n为右手四个手指从矢量A到B旋转θ时大拇指的方向 矢量的叉积是否符合交换律和分配律 不符合交换律, A× B=- B× A 但符合分配律 A(a,b,c)和B(d,e,f)的叉积如何计算 “[\math
《电磁场与电磁波》(谢处方第5版)anki卡片学习笔记txt文件输出
#separator:tab #html:true #tags column:9 矢量叉乘A×B= (用 A、 B的模表示具体的值) e nABsinθ 其中 e n为右手四个手指从矢量A到B旋转θ时大拇指的方向 矢量的叉积是否符合交换律和分配律 不符合交换律, A× B=- B× A 但符合分配律 A(a,b,c)和B(d,e,f)的叉积如何计算 “[\math
电磁场信息论及先进MIMO (黄大年茶思屋座谈) 笔记
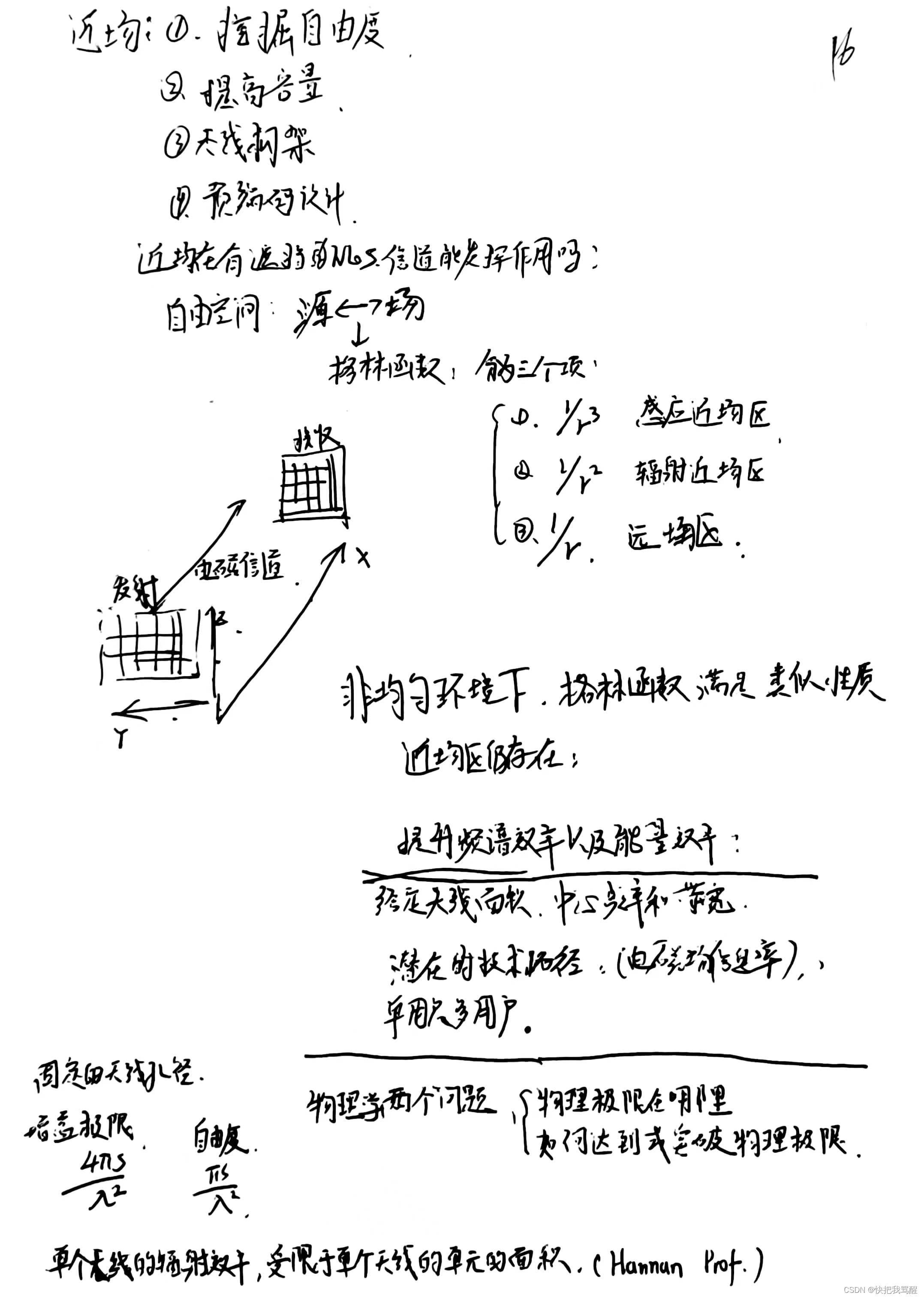
天线阵的负载动态调控,动态阻抗匹配网络,实时跟着扫描角度的变化而变化,可能突破Hannan极限。 新的天线构架: 周期 —》非周期 每个单元不一样 动态可调,可重构 每个天线多端口或多模式 多层天线 非周期结构天线的增益空间 现有的天线的设计没有匹配角谱的特点 22:20/53:37 电磁场信息论及先进MIMO (黄大年茶思屋座谈)
电磁场与电磁波part6、7--均匀平面波的反射与透射、导行电磁波
1、分界面上的反射系数 反射波电场振幅 与入射波电场振幅 的比值,即: 2、驻波系数(驻波比) 合成波的电场强度的最大值与最小值之比,即: 3、导波系统中电磁波的传输问题属于电磁场边值问题,即在给定边界条件下解电磁波动方程。 4、空心导体波导中不能传播TEM波,金属空心波导内可以存在TM波和TE波。 5、模式判断 当工作频率 (工作波长
2021,2022考研电磁场电磁波考研核心题库免费分享
2021,2022考研电磁场电磁波考研核心题库免费分享 具体链接如下: csdn:链接:https://pan.baidu.com/s/1ZePJe2HMjFsYH0QCBPvOxQ 提取码:hfnw 复制这段内容后打开百度网盘手机App,操作更方便哦
matlab 波导场,利用Matlab实现矩形波导电磁场分布图的绘制
利用Matlab实现矩形波导电磁场分布图的绘制 利用 Matlab 实现矩形波导电磁场分布图的绘制(附源程序)通过 Matlab 计算并绘出任意时刻金属矩形波导的主模 TE10 模的电磁场分布图。波导尺寸、工作频率及时刻均由外部给定。A. 矩形波导中传输的主模为 TE10 模。设金属波导尺寸为 a*b,TE10 模的截止波长为2*a。其电磁场分量可推导表示如下:00sinsicosis
电磁场知识整理------2022/12/14
电磁场知识整理 1、数学基础麦克斯韦方程 2、麦克斯韦方程组的近似情况2.1 恒定电场2.2 恒定电流场2.3 恒定磁场2.4 动态电磁场2.5 时谐电磁场 3、电磁辐射与电磁波写在最后 学习资源:慕课上浙大的工程电磁场与波。 工程电磁场与波 1、数学基础 正交坐标系:直角坐标系、柱坐标系、球坐标系。 三度:标量函数的梯度、矢量函数的散度和旋度。 两个重要定理
【你也能看得懂的电磁场与电磁波系列连载 14】
在上一个连载里面,我们通过静磁场的两个基本方程推导出了静磁场的边界条件。 那么今天的连载,我们将给大家看看这种形式的安培环路定理所带来的矛盾。 首先,我们看安培环路定理的左边部分:是磁场的曲线积分,那么讲道理它就应该只跟你这个曲面边界的形状有关。 在安培环路定理里,我们可以随意选一个曲面,然后所有穿过这个曲面的电流会在这个曲面的边界上形成一个环绕磁场。那么这个曲面如何选取就很有意思了。我们
【你也能看得懂的电磁场与电磁波系列连载 13】
在上一个连载里面,我们引入了真空和介质中的安培环路定理。那么这样,我们就可以非常方便地求解某些对称的磁场了。那么很电场类似,在学习磁场时,我们也需要讨论一下磁场的边界条件。 说实话,磁场边界方程的推导和静电场里面的思路几乎一模一样。所以我们这里简单看一看: 我们首先根据静磁场的第一个方程: 那么我们有: n ˉ ⋅ B 1 ˉ − n ˉ ⋅ B 2 ˉ = 0 \bar{n}\sdot