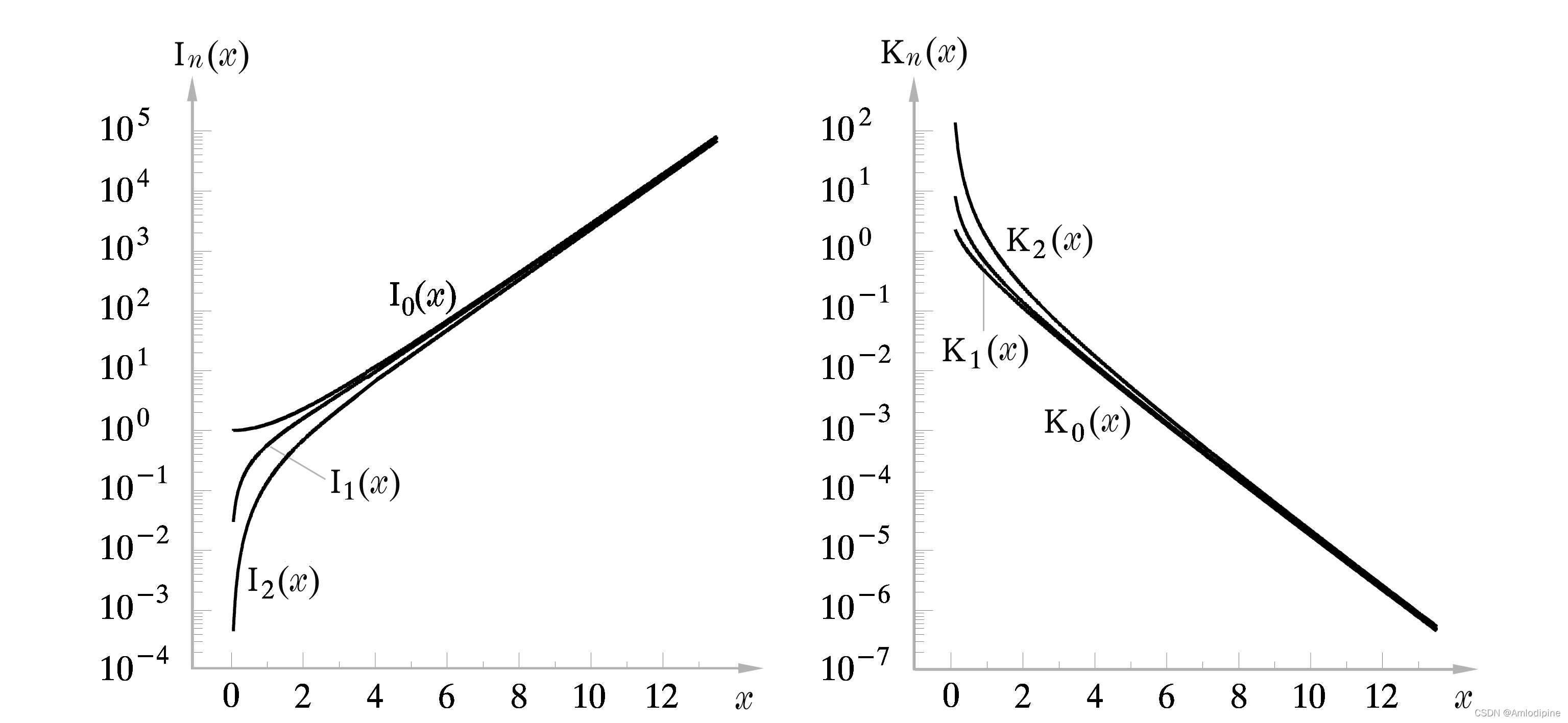
内容 Bessel 函数特殊的 Bessel 函数球 Bessel 函数 Bessel 函数 Bessel 方程的引入 在柱坐标系 ( r , θ , z ) (r,\theta,z) (r,θ,z) 下 Helmholtz 方程 ( ∇ 2 + k 2 ) u = 0 (\nabla^2+k^2)u=0 (∇2+k2)u=0 写为 [ 1 r d d r ( r d d

内容 Legendre 多项式 Legendre 多项式的完备正交归一性对 Legendre 级数展开Legendre 多项式的生成函数 连带 Legendre 多项式球谐函数 正交曲面坐标系下的 Helmholtz 方程 ( ∇ 2 + k 2 ) u = 0 (\nabla^2+k^2)u=0 (∇2+k2)u=0 Legendre 多项式 引入 在球坐标系中对 Helm

03 静电学 目录 问题描述静电势的 Poisson 方程 静电势的一般边界条件导体的边界条件静电边值问题的可解性和解的唯一性 求解静电问题的特殊方法 镜像法分离变量法格林函数法静电的多级展开方法Laplace 方程的数值解法 静电学中的能量和做功 根据介质中的 Maxwell 方程组 ∇ ⋅ D = ρ f ∮ ∂ V d S ⋅ D = Q f ∇ × E = − ∂ B ∂

介绍麦克斯韦方程以及它的一些基本的性质：对称性、守恒律、边界条件等。这是电动力学的一个总纲，也是以后各部分推导的出发点。 内容 真空中的 Maxwell 方程组Maxwell 方程组的性质电介质和磁介质，极化和磁化Maxwell 方程组导出的守恒律电磁场的边界条件 真空中的Maxwell方程 ∇ ⋅ E = ρ ε 0 ( 1 ) （电场的散度定律，高斯定律） ∇ × B = ε

电动力学理论是研究电场和电流的行为和相互作用的物理学分支。电动力学理论可以用于分析和优化电路中的电场和电流分布，特别是在电容和电感的设计和优化中。通过应用电动力学理论，我们可以改善电路的性能，提高电容器和电感器的效率和可靠性。电动力学理论可以用于分析电容器的电场分布。电容器是一种能够存储电荷的装置，由两个导体板之间的绝缘介质隔开。根据电动力学理论，当电容器接通电源时，正电荷会在一个导体板上积累，而

对称性，不变性，相对性，协变形 在现代物理学中常常被认为具有相同的含义（好拗口） 规范与规范的自由度 保证电磁场物理量不改变的情况下，有多组势可供选择，而每组势可以称为一个规范 规范不变性：当势做规范变换时，所有物理量和物理规律都保持不变规范不变性是决定相互作用形式的一条基本原理，传递这些相互作用的场称作规范场 对于电磁场而言，我们由麦克斯韦方程组导出的的电场与磁场的旋度而没有规定其