本文主要是介绍一小时电动力学 02 麦克斯韦方程组,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
介绍麦克斯韦方程以及它的一些基本的性质:对称性、守恒律、边界条件等。这是电动力学的一个总纲,也是以后各部分推导的出发点。
内容
- 真空中的 Maxwell 方程组
- Maxwell 方程组的性质
- 电介质和磁介质,极化和磁化
- Maxwell 方程组导出的守恒律
- 电磁场的边界条件
真空中的Maxwell方程
∇ ⋅ E = ρ ε 0 ( 1 ) (电场的散度定律,高斯定律) ∇ × B = ε 0 μ 0 ∂ E ∂ t + μ 0 J ( 2 ) (磁场的旋度定律,安培环路定律加位移电流假设) ∇ × E = − ∂ B ∂ t ( 3 ) (电场的旋度定律,法拉第电磁感应定律) ∇ ⋅ B = 0 ( 4 ) (磁场的散度定律,无名) \begin{aligned} \nabla\cdot\boldsymbol{E}&=\frac{\rho}{\varepsilon_0}\quad&(1)&\quad\text{(电场的散度定律,高斯定律)}\\ \nabla\times\boldsymbol{B}&=\varepsilon_0\mu_0\frac{\partial\boldsymbol{E}}{\partial t}+\mu_0\boldsymbol{J}\quad&(2)&\quad\text{(磁场的旋度定律,安培环路定律加位移电流假设)}\\ \nabla\times\boldsymbol{E}&=-\frac{\partial\boldsymbol{B}}{\partial t}\quad&(3)&\quad\text{(电场的旋度定律,法拉第电磁感应定律)}\\ \nabla\cdot\boldsymbol{B}&=0\quad&(4)&\quad\text{(磁场的散度定律,无名)} \end{aligned} ∇⋅E∇×B∇×E∇⋅B=ε0ρ=ε0μ0∂t∂E+μ0J=−∂t∂B=0(1)(2)(3)(4)(电场的散度定律,高斯定律)(磁场的旋度定律,安培环路定律加位移电流假设)(电场的旋度定律,法拉第电磁感应定律)(磁场的散度定律,无名)
- 矢量场 ( E , B ) (\boldsymbol{E},\boldsymbol{B}) (E,B) 是某个时空点的电场强度和磁感应强度,它们共同描述了真空中的电磁场。
- ρ \rho ρ 和 J \boldsymbol{J} J 是产生电磁场的电荷密度和电流密度。它们允许包含广义函数,如 Heaviside 阶跃函数和 Dirac 冲激函数,以表示分立的电荷或电流。
- ε 0 \varepsilon_0 ε0 和 μ 0 \mu_0 μ0 分别称为真空中的介电常数和磁导率。
- ( 1 ) , ( 4 ) (1),(4) (1),(4) 对体积元 d τ {\rm d}\tau dτ 积分、 ( 2 ) , ( 3 ) (2),(3) (2),(3) 点乘面积元 d S {\rm d}\boldsymbol{S} dS 积分,就得到 Maxwell 方程组的积分形式。
如果把场量 B , E \boldsymbol{B},\boldsymbol{E} B,E 全部移项到等式的一侧,就得到线性方程组的形式,它的物理意义是:给定的电荷分布 ρ \rho ρ 和电流分布 J \boldsymbol{J} J 在空间中产生电磁场。
根据电荷守恒原理,既然自由电荷和自由电流之间已经存在关系 ∂ ρ ∂ t = − ∇ ⋅ J \cfrac{\partial\rho}{\partial t}=-\nabla\cdot\boldsymbol{J} ∂t∂ρ=−∇⋅J ,为什么在Maxwell方程中还要同时给出 ( ρ , J ) (\rho,\boldsymbol{J}) (ρ,J) 呢?或者,电磁场量能否只由 ρ \rho ρ 或者 J \boldsymbol{J} J 单独决定?
一种解释是 ,只有运动电荷(即电流)才能产生磁场和感受磁场。
洛伦兹力公式
空间中单位体积的电荷和电流分布所受的电磁力(即 洛伦兹力密度 )为
f = ρ E + J × B \boldsymbol{f}=\rho\boldsymbol{E}+\boldsymbol{J}\times\boldsymbol{B} f=ρE+J×B
由于 J = n e v ∥ v \boldsymbol{J}=ne\boldsymbol{v}\parallel\boldsymbol{v} J=nev∥v ,磁场力对洛伦兹力功率没有贡献。
Maxwell方程的性质
线性性质
Maxwell方程是场量 E \boldsymbol{E} E 和 B \boldsymbol{B} B 的线性方程,这表明电磁场满足 线性叠加原理 :若 ( ρ 1 , J 1 ) (\rho_1,\boldsymbol{J}_1) (ρ1,J1) 激发 ( E 1 , B 1 ) (\boldsymbol{E}_1,\boldsymbol{B}_1) (E1,B1) , ( ρ 2 , J 2 ) (\rho_2,\boldsymbol{J}_2) (ρ2,J2) 激发 ( E 2 , B 2 ) (\boldsymbol{E}_2,\boldsymbol{B}_2) (E2,B2) ,它们同时存在时必然激发出 ( E 1 + E 2 , B 1 + B 2 ) (\boldsymbol{E}_1+\boldsymbol{E}_2,\boldsymbol{B}_1+\boldsymbol{B}_2) (E1+E2,B1+B2) 。
- 有线性性质,所以可以用格林函数方法求解电磁场。
- 考虑量子效应后,这种线性叠加性质被破坏。
洛伦兹协变性
麦克斯韦方程在不同惯性参照系之间的洛伦兹变换下保持形式不变。
这导致 k E k B = c 2 \cfrac{k_E}{k_B}=c^2 kBkE=c2 ,其中
- k E k_E kE 为相距单位距离的两单位电荷之间的库仑力的数值
- k B k_B kB 为相距单位距离的一对无限长平行直导线上流有单位强度电流,其中一根导线在单位长度上受到另一导线力的数值(国际单位制)
F E = k E q q ′ r 2 d F B = 2 k B I I ′ r d l \begin{aligned} F_E&=k_E\frac{qq^\prime}{r^2}\\ {\rm d}F_B&=2k_B\frac{II^\prime}{r}{\rm d}l \end{aligned} FEdFB=kEr2qq′=2kBrII′dl
规范不变性
即 规范对称性 。在经典电动力学中,规范对称性是通过所谓的电磁势来体现的。
对于 ∇ ⋅ B = 0 \nabla\cdot\boldsymbol{B}=0 ∇⋅B=0 ,根据恒等式 ∇ ⋅ ( ∇ × A ) ≡ 0 \nabla\cdot(\nabla\times\boldsymbol{A})\equiv 0 ∇⋅(∇×A)≡0 ,可以令磁感应强度 B = ∇ × A \boldsymbol{B}=\nabla\times\boldsymbol{A} B=∇×A ,其中 A \boldsymbol{A} A 称为 矢势 。代入 ∇ × E = − ∂ B ∂ t \nabla\times\boldsymbol{E}=-\cfrac{\partial\boldsymbol{B}}{\partial t} ∇×E=−∂t∂B ,就得到 ∇ × ( E + ∂ A ∂ t ) = 0 \nabla\times\left(\boldsymbol{E}+\cfrac{\partial\boldsymbol{A}}{\partial t}\right)=0 ∇×(E+∂t∂A)=0 。
再根据恒等式 ∇ × ( ∇ Φ ) ≡ 0 \nabla\times(\nabla\Phi)\equiv 0 ∇×(∇Φ)≡0 ,可以令 E + ∂ A ∂ t = − ∇ Φ \boldsymbol{E}+\cfrac{\partial\boldsymbol{A}}{\partial t}=-\nabla\Phi E+∂t∂A=−∇Φ ,其中 Φ \Phi Φ 称为标势。这样就得到
B = ∇ × A E = − ∂ A ∂ t − ∇ Φ \begin{aligned} \boldsymbol{B}&=\nabla\times\boldsymbol{A}\\ \boldsymbol{E}&=-\cfrac{\partial\boldsymbol{A}}{\partial t}-\nabla\Phi \end{aligned} BE=∇×A=−∂t∂A−∇Φ
给定 E , B \boldsymbol{E},\boldsymbol{B} E,B 并不足以确定 ( A , Φ ) (\boldsymbol{A},\Phi) (A,Φ) 。事实上 ∀ φ = φ ( r , t ) \forall\varphi=\varphi(\boldsymbol{r},t) ∀φ=φ(r,t) :
A ′ = A + ∇ φ Φ ′ = Φ − ∂ φ ∂ t \begin{aligned} \boldsymbol{A}^\prime&=\boldsymbol{A}+\nabla\varphi\\ \Phi^\prime&=\Phi-\cfrac{\partial\varphi}{\partial t} \end{aligned} A′Φ′=A+∇φ=Φ−∂t∂φ
给出的 ( A ′ , Φ ′ ) (\boldsymbol{A}^\prime,\Phi^\prime) (A′,Φ′) 也适合上面电磁势的定义。
电磁场所具有的这种对称性(不变性)被称为规范对称性。等式 ( A , Φ ) → ( A ′ , Φ ′ ) (\boldsymbol{A},\Phi)\to(\boldsymbol{A}^\prime,\Phi^\prime) (A,Φ)→(A′,Φ′) 所描写的两套等价的电磁势之间的变换称为 规范变换 。
这表明在经典电动力学过程中,电磁势本身不可直接测量,所有可以直接测量的物理量都仅仅与电磁场,而不是电磁势有关。
考虑量子力学后有反例如 A-B 效应。
取决于所处理的问题的不同,可以为电磁势加条件将其完全确定,这一类条件通称为 规范条件 ,这一步骤叫 定规范 ,满足一定规范条件的电磁势就被称为某种规范中的电磁势。
洛伦兹规范
又被称为协变规范。其条件是
∇ ⋅ A + 1 c 2 ∂ Φ ∂ t = 0 \nabla\cdot\boldsymbol{A}+\frac1{c^2}\frac{\partial\Phi}{\partial t}=0 ∇⋅A+c21∂t∂Φ=0
库伦规范
也叫辐射规范、模规范。其条件是
∇ ⋅ A = 0 \nabla\cdot\boldsymbol{A}=0 ∇⋅A=0
根据矢量场的 Helmholtz 定理,矢量场可以由旋度和散度确定。上面两种规范都给出了 ∇ ⋅ A \nabla\cdot\boldsymbol{A} ∇⋅A 。
后面会看到,选用合适的规范可以简化讨论的问题。
解的波动性
电磁势自动满足方程 ( 3 ) , ( 4 ) (3),(4) (3),(4) 。用电磁势代换 E , B \boldsymbol{E},\boldsymbol{B} E,B ,并采用洛伦兹规范,方程 ( 1 ) , ( 2 ) (1),(2) (1),(2) 化为关于电磁势的独立的波动方程:
− ∇ ⋅ E = ∇ ⋅ ( ∇ Φ + ∂ A ∂ t ) = ∇ 2 Φ + ∂ ∂ t ( ∇ ⋅ A ) = ∇ 2 Φ − 1 c 2 ∂ 2 Φ ∂ t 2 = − ρ ε 0 ( 1 ∗ ) ∇ × B − 1 c 2 ∂ E ∂ t = ∇ × ( ∇ × A ) + 1 c 2 ∂ ∂ t ( ∇ Φ + ∂ A ∂ t ) = [ ∇ ( ∇ ⋅ A ) − ∇ 2 A ] + [ − ∇ ( ∇ ⋅ A ) + 1 c 2 ∂ 2 A ∂ 2 t ] = − ∇ 2 A + 1 c 2 ∂ 2 A ∂ t 2 = μ 0 J ( 2 ∗ ) \begin{aligned} -\nabla\cdot\boldsymbol{E}&=\nabla\cdot\left(\nabla\Phi+\frac{\partial\boldsymbol{A}}{\partial t}\right)\\ &=\nabla^2\Phi+\frac{\partial}{\partial t}\left(\nabla\cdot\boldsymbol{A}\right)\\ &={\color{DarkRed}\nabla^2\Phi-\frac{1}{c^2}\frac{\partial^2\Phi}{\partial t^2}=-\frac{\rho}{\varepsilon_0}}\quad&(1^*)\\ \nabla\times\boldsymbol{B}-\frac{1}{c^2}\frac{\partial\boldsymbol{E}}{\partial t} &=\nabla\times\left(\nabla\times\boldsymbol{A}\right)+\frac{1}{c^2}\frac{\partial}{\partial t}\left(\nabla\Phi+\frac{\partial\boldsymbol{A}}{\partial t}\right)\\ &=\bigg[\nabla\left(\nabla\cdot\boldsymbol{A}\right)-\nabla^2\boldsymbol{A}\bigg]+\left[-\nabla(\nabla\cdot\boldsymbol{A})+\frac{1}{c^2}\frac{\partial^2\boldsymbol{A}}{\partial ^2t}\right]\\ &={\color{DarkRed}-\nabla^2\boldsymbol{A}+\frac{1}{c^2}\frac{\partial^2\boldsymbol{A}}{\partial t^2}=\mu_0\boldsymbol{J}}\quad&(2^*) \end{aligned} −∇⋅E∇×B−c21∂t∂E=∇⋅(∇Φ+∂t∂A)=∇2Φ+∂t∂(∇⋅A)=∇2Φ−c21∂t2∂2Φ=−ε0ρ=∇×(∇×A)+c21∂t∂(∇Φ+∂t∂A)=[∇(∇⋅A)−∇2A]+[−∇(∇⋅A)+c21∂2t∂2A]=−∇2A+c21∂t2∂2A=μ0J(1∗)(2∗)
它表明电磁势(从而电磁场)具有波动形式的解。这种波被称为 电磁波 ,其在真空中的波速为 c c c ,与真空中的光速吻合。
分立对称性
在此主要讨论两类:空间反射(宇称)不变性、时间反演不变性。
- 空间反射变换
把所有的空间坐标都改变符号: x i → − x i x_i\to-x_i xi→−xi ,则:
ρ → ρ J → − J r → − r t → t ∇ → − ∇ = e ^ i ∂ ∂ ( − x i ) ( ∗ ) \begin{aligned} \rho&\to\rho\\ \boldsymbol{J}&\to-\boldsymbol{J}\\ \boldsymbol{r}&\to-\boldsymbol{r}\\ t&\to t\\ \nabla&\to-\nabla=\boldsymbol{\hat e}_i\frac{\partial}{\partial(-x_i)}\quad&(*) \end{aligned} ρJrt∇→ρ→−J→−r→t→−∇=e^i∂(−xi)∂(∗)
( ∗ ) (*) (∗) 位矢不是系统的物理量,坐标才是。事实上对系统做变换,等价于对坐标架作反向的变换。
此处是对系统作变换。
那么
E → − E B → B \begin{aligned}\boldsymbol{E}&\to-\boldsymbol{E}\\\boldsymbol{B}&\to\boldsymbol{B}\end{aligned} EB→−E→B
一般将位矢、电场强度这类在空间反射下变号的矢量称为 极矢量 ,将磁场这类在空间反射下不变的矢量称为 轴矢量 ( 赝矢量 )。因为负负得正,极矢量叉乘极矢量得到轴矢量。
极矢量和轴矢量也可以在镜像对称性中定义。镜像操作指系统对某个平面作镜像反射,若操作前后系统的时空位置等物理状态不变就称其具有某种镜像对称性。
若一矢量作镜像操作后,镜面的平行分量不变而垂直分量反号,则称为极矢量;反之若平行分量反号而垂直分量不变,则称为轴矢量(赝矢量)。
这种定义方式和上面的实际上一致,不过镜像反射一次只改变一个坐标分量的符号。
【例】 r , v , a , E , D \boldsymbol{r},\boldsymbol{v},\boldsymbol{a},\boldsymbol{E},\boldsymbol{D} r,v,a,E,D 是极矢量; ω , L , B , H \boldsymbol{\omega},\boldsymbol{L},\boldsymbol{B},\boldsymbol{H} ω,L,B,H 是轴矢量。
一个有意义的应用是,若某系统有镜像对称,考察物理量在镜面上的分布,极矢量只有平行分量,轴矢量只有垂直分量。
- 时间反演变换
就是 t → − t t\to-t t→−t 的变换。注意此时 ∂ ∂ t → ∂ ∂ ( − t ) = − ∂ ∂ t \cfrac{\partial}{\partial t}\to\cfrac{\partial}{\partial(-t)}=-\cfrac{\partial}{\partial t} ∂t∂→∂(−t)∂=−∂t∂ ,所以速度变号,加速度不变号。容易推出
E → E B → − B \begin{aligned}\boldsymbol{E}&\to\boldsymbol{E}\\\boldsymbol{B}&\to-\boldsymbol{B}\end{aligned} EB→E→−B
介质中的Maxwell方程
原则上,如果以原子尺度来考虑问题,那么所谓介质无非是大量的、不断运动的微观粒子的集合体。这些微观粒子一般都带有电荷或磁矩。因此,介质中的电磁场原则上是外加电磁场和这些介质中的微观粒子所产生的电磁场线性叠加后,再进行某种统计平均的结果。
现代物理学告诉我们,微观粒子从本质上说遵从 量子力学 而不是经典力学。因此,从微观第一原理出发处理介质中的电磁现象将是量子力学和统计物理的课题。在经典电动力学范围内,我们将满足于一个经典的、而且很多情形下是 唯象 的描述。
需要说明,该方程组相比真空中的形式,没有具有更多的物理内涵。我们只是把电荷、电流分成自由的和不自由的两部分,并定义了两个新的物理量 D \boldsymbol{D} D 和 H \boldsymbol{H} H 。
电介质
一对等量反号电荷 ± q \pm q ±q 彼此靠近,就构成一个电偶极子,其物理特征量是 电偶极矩 p = q d \boldsymbol{p}=q\boldsymbol{d} p=qd ,其中 d \boldsymbol{d} d 是正电荷 + q +q +q 相对负电荷的位移矢量。
首先考虑所谓线性、各向同性、均匀的介质。在外加电场 E \boldsymbol{E} E 的作用下,介质分子发生极化,出现束缚电荷 Q b Q_b Qb 的分布 ρ b \rho_b ρb ,电介质单位体积的平均电偶极矩会不为0。具体可以定义单位体积中的平均电偶极矩为 电极化强度 P \boldsymbol{P} P ,即 P V ‾ = 1 V ∑ p \overline{\boldsymbol{P}_V}=\cfrac{1}{V}\sum\boldsymbol{p} PV=V1∑p 。
设介质中的小区域 V V V 由封闭曲面包围。电偶极矩由负电荷指向正电荷,所以束缚电荷的分布 ρ b \rho_b ρb 满足
∫ V ρ b d 3 r = Q b = − ∮ ∂ V P ⋅ n ^ d S ρ b = − ∇ ⋅ P \begin{aligned} \int_V\rho_b{\rm d}^3\boldsymbol{r}=Q_b&=-\oint_{\partial V}\boldsymbol{P}\cdot\boldsymbol{\hat n}{\rm d}S\\ \rho_b&=-\nabla\cdot\boldsymbol{P} \end{aligned} ∫Vρbd3r=Qbρb=−∮∂VP⋅n^dS=−∇⋅P
其中 n ^ \boldsymbol{\hat n} n^ 是单位外法矢。在介质的边缘处(假设外侧是真空),束缚面电荷分布 σ b = n ⋅ P \sigma_b=\boldsymbol{n}\cdot\boldsymbol{P} σb=n⋅P 。
如果束缚电荷密度分布 ρ b \rho_b ρb 随时间改变,就会有 束缚电流密度 ,记为 J b \boldsymbol{J}_b Jb 。束缚电荷也要服从电荷守恒(即电荷连续性方程),所以
∂ ρ b ∂ t + ∇ ⋅ J b = 0 \frac{\partial\rho_b}{\partial t}+\nabla\cdot\boldsymbol{J}_b=0 ∂t∂ρb+∇⋅Jb=0
消去 ρ b \rho_b ρb 就推出 J b = ∂ P ∂ t \boldsymbol{J}_b=\cfrac{\partial\boldsymbol{P}}{\partial t} Jb=∂t∂P 。
磁介质
一个平面电流环构成一个磁偶极子,其特征量磁(偶极)矩 m = I S n ^ \boldsymbol{m}=IS\boldsymbol{\hat n} m=ISn^ ,其中单位法向 n ^ \boldsymbol{\hat n} n^ 由电流流向根据右手法则确定。
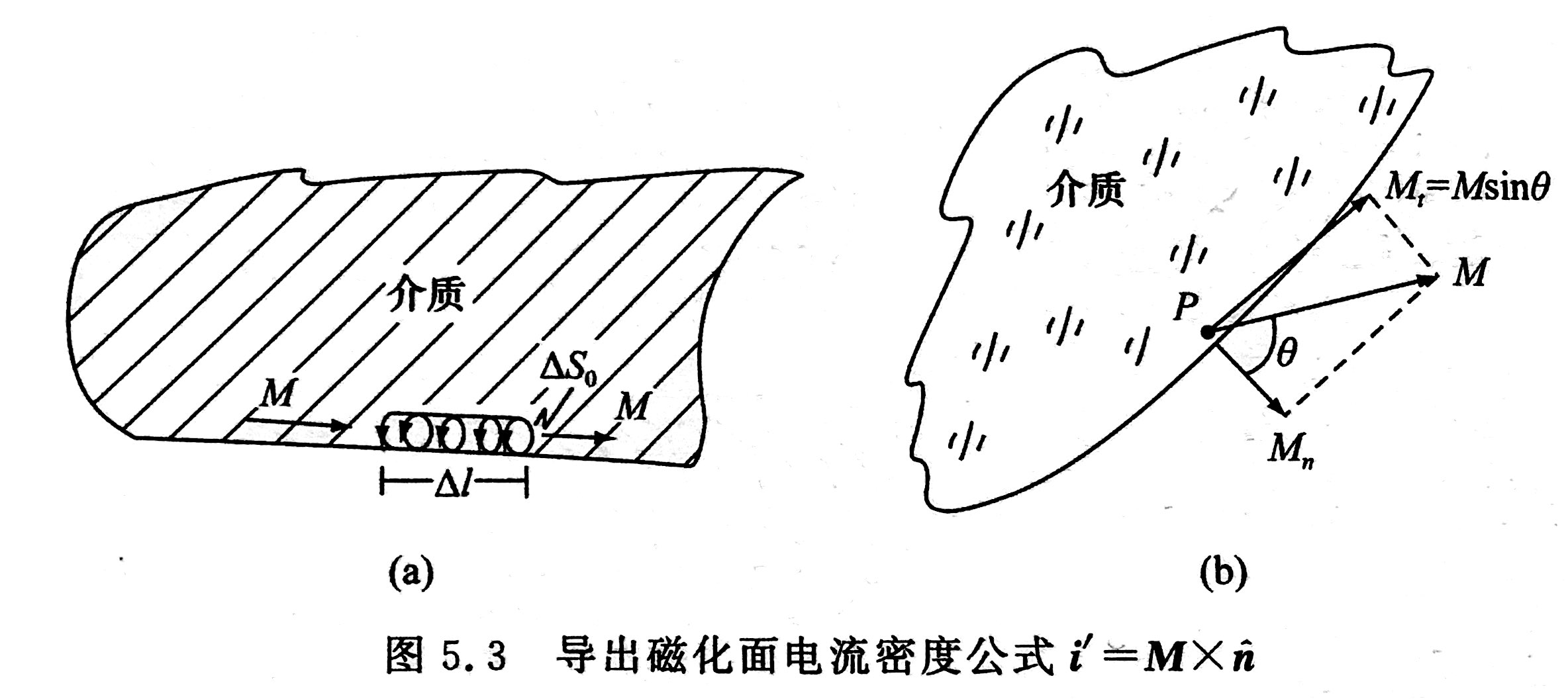
磁偶极子具有磁矩 m \boldsymbol{m} m ,类似地在介质被磁化时,单位体积的平均磁矩称为 磁化强度 M \boldsymbol{M} M 。介质内部存在运动的微观带电粒子,这会产生一个电流密度分布,称为 分子电流密度 J m \boldsymbol{J}_m Jm ,亦即磁化体电流密度。
在介质中取一个由无穷小闭合回路围成的面积元 S S S ,记面积元的单位法向为 n ^ \boldsymbol{\hat n} n^ ,就有
∫ S J m ⋅ n ^ d S = I m = ∮ ∂ S M ⋅ d l \int_S\boldsymbol{J}_m\cdot\boldsymbol{\hat n}{\rm d}S=I_m=\oint_{\partial S}\boldsymbol{M}\cdot{\rm d}\boldsymbol{l} ∫SJm⋅n^dS=Im=∮∂SM⋅dl
其中 d S {\rm d}S dS 的正向与 n ^ \boldsymbol{\hat n} n^ 一致。

所以 J m = ∇ × M \boldsymbol{J}_m=\nabla\times\boldsymbol{M} Jm=∇×M ,在介质表面的分子电流面密度 K m = − n ^ × M \boldsymbol{K}_m=-\boldsymbol{\hat n}\times\boldsymbol{M} Km=−n^×M 。
方程的改写
方程组中的齐次方程显然不需改动。只需做替换 ρ → ρ + ρ b \rho\to\rho+\rho_b ρ→ρ+ρb 和 J → J + J b + J m \boldsymbol{J}\to\boldsymbol{J}+\boldsymbol{J}_b+\boldsymbol{J}_m J→J+Jb+Jm ,也就是
∇ ⋅ E = 1 ε 0 ( ρ − ∇ ⋅ P ) ( 1 † ) ∇ × B = ε 0 μ 0 ∂ E ∂ t + μ 0 ( J + ∂ P ∂ t + ∇ × M ) ( 2 † ) \begin{aligned} \nabla\cdot\boldsymbol{E}&=\frac{1}{\varepsilon_0}\left(\rho-\nabla\cdot\boldsymbol{P}\right)\quad&(1^\dagger)\\ \nabla\times\boldsymbol{B}&={\varepsilon_0\mu_0}\frac{\partial\boldsymbol{E}}{\partial t}+\mu_0\left(\boldsymbol{J}+\frac{\partial\boldsymbol{P}}{\partial t}+\nabla\times\boldsymbol{M}\right)\quad&(2^\dagger) \end{aligned} ∇⋅E∇×B=ε01(ρ−∇⋅P)=ε0μ0∂t∂E+μ0(J+∂t∂P+∇×M)(1†)(2†)
极化强度是不易观测的量,定义 电位移(也作 电势移 ) D = ε 0 E + P \boldsymbol{D}=\varepsilon_0\boldsymbol{E}+\boldsymbol{P} D=ε0E+P 、 磁场强度 H = 1 μ 0 B − M \boldsymbol{H}=\cfrac{1}{\mu_0}\boldsymbol{B}-\boldsymbol{M} H=μ01B−M ,方程就改写成了
∇ ⋅ D = ρ ( 1 † ) ∇ × H = ∂ D ∂ t + J ( 2 † ) ∇ × E = − ∂ B ∂ t ( 3 † ) ∇ ⋅ B = 0 ( 4 † ) \begin{aligned} \nabla\cdot\boldsymbol{D}&=\rho\quad&(1^\dagger)\\ \nabla\times\boldsymbol{H}&=\frac{\partial\boldsymbol{D}}{\partial t}+\boldsymbol{J}\quad&(2^\dagger)\\ \nabla\times\boldsymbol{E}&=-\frac{\partial\boldsymbol{B}}{\partial t}\quad&(3^\dagger)\\ \nabla\cdot\boldsymbol{B}&=0\quad&(4^\dagger) \end{aligned} ∇⋅D∇×H∇×E∇⋅B=ρ=∂t∂D+J=−∂t∂B=0(1†)(2†)(3†)(4†)
需要说明的是,方程 D = D [ E , B ] = ε 0 E + P \boldsymbol{D}=\boldsymbol{D}[\boldsymbol{E},\boldsymbol{B}]=\varepsilon_0\boldsymbol{E}+\boldsymbol{P} D=D[E,B]=ε0E+P 和 H = H [ E , B ] = 1 μ 0 B − M \boldsymbol{H}=\boldsymbol{H}[\boldsymbol{E},\boldsymbol{B}]=\cfrac{1}{\mu_0}\boldsymbol{B}-\boldsymbol{M} H=H[E,B]=μ01B−M 是十分简化的模型。对于实际情况,以上关系可以十分复杂,可以是非线性甚至(时空)非局域的。这称为介质中的 本构关系 ( 本构方程 )。
线性介质
定义 线性介质 ,它满足这样的条件:
P i ( t ) = ε 0 ∫ − ∞ + ∞ χ i j ( e ) ( τ ) E j ( t − τ ) d τ ≡ ε 0 χ i j ( e ) ⊗ E j M i ( t ) = ∫ − ∞ + ∞ χ i j ( m ) ( τ ) H j ( t − τ ) d τ ≡ χ i j ( m ) ⊗ H j \begin{aligned} P_i(t)=\varepsilon_0\int_{-\infty}^{+\infty}\chi_{ij}^{(e)}(\tau)E_j(t-\tau){\rm d}\tau\equiv\varepsilon_0\chi_{ij}^{(e)}\otimes E_j\\ M_i(t)=\int_{-\infty}^{+\infty}\chi_{ij}^{(m)}(\tau)H_j(t-\tau){\rm d}\tau\equiv\chi_{ij}^{(m)}\otimes H_j \end{aligned} Pi(t)=ε0∫−∞+∞χij(e)(τ)Ej(t−τ)dτ≡ε0χij(e)⊗EjMi(t)=∫−∞+∞χij(m)(τ)Hj(t−τ)dτ≡χij(m)⊗Hj
其中 ⊗ \otimes ⊗ 是卷积。说明:
-
这里假设了 D \boldsymbol{D} D 只线性依赖于 E \boldsymbol{E} E 、 H \boldsymbol{H} H 只线性依赖于 B \boldsymbol{B} B ,也就是说不存在电和磁之间的“混合作用”,多数情形这是正确的。唯一的常见例外是介质本身在运动的情形。
-
这是一个较普遍的线性关系,它们对于时间不是局域的, P , M \boldsymbol{P},\boldsymbol{M} P,M 依赖于 E , H \boldsymbol{E},\boldsymbol{H} E,H 的历史。
因果性要求 χ i j ( t ) ≡ 0 ∀ t < 0 \chi_{ij}(t)\equiv0\quad\forall t<0 χij(t)≡0∀t<0 。
最为普遍的线性关系还可包含空间的不局域性:一点的极化情况还可以依赖于空间其他点的外场,这种现象被称为 空间色散 。它仅仅出现在非常特殊的情形下。 -
使用 H \boldsymbol{H} H 而不是 B \boldsymbol{B} B 表示纯属历史问题。
对上式的时间变量作傅里叶变换(系数约定为 χ ( ∗ ) ( t ) = 1 2 π ∫ ω χ ( ∗ ) ( ω ) e − i ω t d ω \chi^{(*)}(t)=\cfrac1{2\pi}\int\limits_\omega\chi^{(*)}(\omega)e^{-i\omega t}{\rm d}\omega χ(∗)(t)=2π1ω∫χ(∗)(ω)e−iωtdω ),就有
P ( ω ) = χ ⃗ ⃗ ( e ) ( ω ) ⋅ E ( ω ) M ( ω ) = χ ⃗ ⃗ ( m ) ( ω ) ⋅ H ( ω ) \begin{aligned} \boldsymbol{P}(\omega)&=\vec{\vec{\chi}}^{(e)}(\omega)\cdot\boldsymbol{E}(\omega)\\ \boldsymbol{M}(\omega)&=\vec{\vec{\chi}}^{(m)}(\omega)\cdot\boldsymbol{H}(\omega) \end{aligned} P(ω)M(ω)=χ(e)(ω)⋅E(ω)=χ(m)(ω)⋅H(ω)
其中定义了 电极化率张量 χ ⃗ ⃗ ( e ) ( ω ) \vec{\vec{\chi}}^{(e)}(\omega) χ(e)(ω) 和 磁化率张量 χ ⃗ ⃗ ( m ) ( ω ) \vec{\vec{\chi}}^{(m)}(\omega) χ(m)(ω) 。代入本构关系就得到
D ( ω ) = ε 0 ( δ i j + χ ⃗ ⃗ ( e ) ( ω ) ) ⋅ E ( ω ) ≡ ε ⃗ ⃗ ( ω ) ⋅ E ( ω ) B ( ω ) = μ 0 ( δ i j + χ ⃗ ⃗ ( m ) ( ω ) ) ⋅ H ( ω ) ≡ μ ⃗ ⃗ ( ω ) ⋅ H ( ω ) \begin{aligned} \boldsymbol{D}(\omega)=\varepsilon_0\left(\delta_{ij}+\vec{\vec{\chi}}^{(e)}(\omega)\right)\cdot\boldsymbol{E}(\omega) \equiv\vec{\vec{\varepsilon}}(\omega)\cdot\boldsymbol{E}(\omega)\\ \boldsymbol{B}(\omega)=\mu_0\left(\delta_{ij}+\vec{\vec{\chi}}^{(m)}(\omega)\right)\cdot\boldsymbol{H}(\omega) \equiv\vec{\vec{\mu}}(\omega)\cdot\boldsymbol{H}(\omega)\\ \end{aligned} D(ω)=ε0(δij+χ(e)(ω))⋅E(ω)≡ε(ω)⋅E(ω)B(ω)=μ0(δij+χ(m)(ω))⋅H(ω)≡μ(ω)⋅H(ω)
其中 ε ⃗ ⃗ \vec{\vec{\varepsilon}} ε 和 μ ⃗ ⃗ \vec{\vec{\mu}} μ 分别称为 介电张量 和 磁导率张量 。它们只与介质的性质有关,不再依赖于电磁场。
对于静态的外场,只要介质不具有电滞或者磁滞现象,那么介质的介电张量和磁导率张量一定是对称张量;对于非静态的情形,利用Onsager的互易关系,也可以证明它是一个对称张量。
如果进一步假设线性介质具有旋转对称性,就成为各向同性的线性介质,介电张量和磁导率张量都退化为与单位张量成正比(其实就约化为一个标量):
χ i j ( e / m ) = χ ( e / m ) δ i j \chi_{ij}^{(e/m)}=\chi^{(e/m)}\delta_{ij} χij(e/m)=χ(e/m)δij
其实只需要立方对称性就可以把张量约化成标量。
这样就会有
D ( ω ) = ε ( ω ) E ( ω ) , ε ( ω ) = ε 0 ( 1 + χ ( e ) ( ω ) ) H ( ω ) = 1 μ ( ω ) B ( ω ) , μ ( ω ) = μ 0 ( 1 + χ ( m ) ( ω ) ) \begin{aligned} \boldsymbol{D}(\omega)&=\varepsilon(\omega)\boldsymbol{E}(\omega),\quad&&\varepsilon(\omega)=\varepsilon_0\left(1+\chi^{(e)}(\omega)\right)\\ \boldsymbol{H}(\omega)&=\frac{1}{\mu(\omega)}\boldsymbol{B}(\omega),\quad&&\mu(\omega)=\mu_0\left(1+\chi^{(m)}(\omega)\right) \end{aligned} D(ω)H(ω)=ε(ω)E(ω),=μ(ω)1B(ω),ε(ω)=ε0(1+χ(e)(ω))μ(ω)=μ0(1+χ(m)(ω))
其中 ε ( ω ) \varepsilon(\omega) ε(ω) 被称为介质的 电容率 或 介电常数 , μ ( ω ) \mu(\omega) μ(ω) 被称为介质的 磁导率 。无量纲参数 χ ( e ) ( ω ) \chi^{(e)}(\omega) χ(e)(ω) 和 χ ( m ) ( ω ) \chi^{(m)}(\omega) χ(m)(ω) 被称为该各向同性线性介质的 电极化率 和 磁化率 。有时候会使用同样无量纲的 相对介电常数 ε r = ε ε 0 \varepsilon_r=\cfrac{\varepsilon}{\varepsilon_0} εr=ε0ε 和 相对磁导率 μ r = μ μ 0 \mu_r=\cfrac{\mu}{\mu_0} μr=μ0μ 。
特殊的介质
铁电体和铁磁体
在外电场或外磁场是零的时候它也存在自发的电极化或磁化。是非线性介质!所以不适用张量式 P = χ ( e ) ⋅ E \boldsymbol{P}=\chi^{(e)}\cdot\boldsymbol{E} P=χ(e)⋅E , M = χ ( m ) ⋅ H \boldsymbol{M}=\chi^{(m)}\cdot\boldsymbol{H} M=χ(m)⋅H ,但仍适用定义式 D = ε 0 E + P \boldsymbol{D}=\varepsilon_0\boldsymbol{E}+\boldsymbol{P} D=ε0E+P , H = 1 μ 0 B − M \boldsymbol{H}=\cfrac{1}{\mu_0}\boldsymbol{B}-\boldsymbol{M} H=μ01B−M 。
一类重要铁磁体是所谓的硬铁磁体,这种介质的磁化强度 M \boldsymbol{M} M 几乎不依赖于外磁场。
顺磁性和抗(逆)磁性
对于线性各向同性介质,磁化率为正称为 顺磁性 ,磁化率为负称为 抗磁性 。各向同性的线性介质,电极化率永远是正的。
导体
比如金属、导电溶液、电离的等离子体等等。这一类介质在电场中会相应地产生宏观的电流。这种电流的流动一般伴随着热耗散的产生。
导电性是固体物理主要研究的问题。这里假设设电流密度 J \boldsymbol{J} J 与电场 E \boldsymbol{E} E 有线性关系,并把这种普遍的线性关系唯象地写成
J ( ω ) = σ ⃗ ⃗ ( ω ) ⋅ E ( ω ) \boldsymbol{J}(\omega)=\vec{\vec{\sigma}}(\omega)\cdot\boldsymbol{E}(\omega) J(ω)=σ(ω)⋅E(ω)
如果介质各向同性,张量 σ ⃗ ⃗ ( ω ) \vec{\vec{\sigma}}(\omega) σ(ω) 就退化为单位张量的若干倍,其比例系数就是 电导率 σ ( ω ) \sigma(\omega) σ(ω) ,也就得到了常见的欧姆定律形式 J ( ω ) = σ ( ω ) E ( ω ) \boldsymbol{J}(\omega)=\sigma(\omega)\boldsymbol{E}(\omega) J(ω)=σ(ω)E(ω) 。
理想导体是 σ → + ∞ \sigma\to+\infty σ→+∞ 的介质,一个实际的例子就是 超导体 。其内部 E = B ≡ 0 \boldsymbol{E}=\boldsymbol{B}\equiv\boldsymbol{0} E=B≡0 。
介质的边界
在两种不同介质的交界面附近,电磁场必须满足一定的边界条件,这些边界条件可以从积分形式的麦克斯韦方程得到。
如果知道了介质的本构方程、自由电荷和(自由?)电流的分布、边界条件,根据偏微分方程理论,满足麦克斯韦方程的电磁场就被唯一地确定了。
另外,边界条件还是定量处理电磁波在介质界面处反射和折射的重要基础。
法向分量与“高斯小盒”
在介质界面上任一点构造底面与该点法向方向垂直、高度为无穷小的柱体。柱体的两个底面分别处于两种介质之中,底面积为 Δ S \Delta{S} ΔS 。
将方程 ( 1 † ) (1^\dagger) (1†) 积分,就得到
σ Δ S = ∫ V d 3 r ( ∇ ⋅ D ) = ∮ ∂ V D ⋅ d S = Δ S ( D 2 − D 1 ) ⋅ n ^ D n 2 − D n 1 = σ \begin{aligned} \sigma\Delta{S}=\int_V{\rm d}^3\boldsymbol{r}(\nabla\cdot\boldsymbol{D})=&\oint_{\partial V}\boldsymbol{D}\cdot{\rm d}\boldsymbol{S}=\Delta{S}(\boldsymbol{D}_2-\boldsymbol{D}_1)\cdot{\boldsymbol{\hat n}}\\ D_{n2}-D_{n1}&=\sigma \end{aligned} σΔS=∫Vd3r(∇⋅D)=Dn2−Dn1∮∂VD⋅dS=ΔS(D2−D1)⋅n^=σ
以上设一个单位法向量 n ^ \boldsymbol{\hat n} n^ 由介质 1 1 1 指向介质 2 2 2 ,曲面积分取向外为正向,则外法矢 d S 1 = − n ^ d S {\rm d}\boldsymbol{S}_1=-\boldsymbol{\hat n}{\rm d}S dS1=−n^dS , d S 2 = n ^ d S {\rm d}\boldsymbol{S}_2=\boldsymbol{\hat n}{\rm d}S dS2=n^dS 。
这表明面(自由)电荷分布导致界面上电位移法向分量 D n D_n Dn 的不连续性。
类似地可以得到磁感应强度的法向分量在介质边界处满足 B n 2 − B n 1 = 0 B_{n2}-B_{n1}=0 Bn2−Bn1=0 ,亦即 B \boldsymbol{B} B 的法向分量连续。
切向分量与“安培小圈”
在两种介质的交界面处构造一个无穷小的矩形回路,使得其中一组对边平行于界面、而分别位于两种介质中,另一组对边的长为前一组边长的高阶无穷小。将方程 ( 3 † ) (3^\dagger) (3†) 积分,就得到
∮ ∂ S E ⋅ d l = ∫ S ( ∇ × E ) ⋅ d S = − ∫ S ∂ B ∂ t ⋅ d S \oint_{\partial S}\boldsymbol{E}\cdot{\rm d}\boldsymbol{l} =\int_S({\nabla\times\boldsymbol{E}})\cdot{\rm d}\boldsymbol{S} =-\int_S\frac{\partial\boldsymbol{B}}{\partial t}\cdot{\rm d}\boldsymbol{S} ∮∂SE⋅dl=∫S(∇×E)⋅dS=−∫S∂t∂B⋅dS
其中曲线积分的正向和面积分中面积微元的法矢方向一致。环路的面积 S S S 是高阶小量,磁感应强度变化率 ∂ B ∂ t \cfrac{\partial\boldsymbol{B}}{\partial t} ∂t∂B 有限,所以 ∫ S ∂ B ∂ t ⋅ d S → 0 \int\limits_S\cfrac{\partial\boldsymbol{B}}{\partial t}\cdot{\rm d}\boldsymbol{S}\to0 S∫∂t∂B⋅dS→0 ,就得到
n ^ × ( E 2 − E 1 ) = 0 \boldsymbol{\hat{n}}\times(\boldsymbol{E}_2-\boldsymbol{E}_1)=0 n^×(E2−E1)=0
上述矢量叉乘等于零的直接理解是 E 1 − E 2 \boldsymbol{E}_1-\boldsymbol{E}_2 E1−E2 和法向量平行,从而没有切向分量;再要么直接有 E 1 = E 2 \boldsymbol{E}_1=\boldsymbol{E}_2 E1=E2 。严格的解释是因为
E 1 τ − E 2 τ = ( n ^ × ( E 1 − E 2 ) ) × n ^ = 0 \boldsymbol{E}_1^\tau-\boldsymbol{E}_2^\tau=\big(\boldsymbol{\hat n}\times(\boldsymbol{E}_1-\boldsymbol{E}_2)\big)\times\boldsymbol{\hat n}=0 E1τ−E2τ=(n^×(E1−E2))×n^=0
类似地从方程 ( 4 † ) (4^\dagger) (4†) 可以得到 n ^ × ( H 1 − H 2 ) = K f \boldsymbol{\hat n}\times(\boldsymbol{H}_1-\boldsymbol{H}_2)=\boldsymbol{K}_f n^×(H1−H2)=Kf 。
亦用到矢量恒等式
( n ^ × A ) × n ^ = A τ A × n ^ × n ^ = − A τ \begin{aligned} (\boldsymbol{\hat n}\times\boldsymbol{A})\times\boldsymbol{\hat n}&=\boldsymbol{A}_\tau\\ \boldsymbol{A}\times\boldsymbol{\hat n}\times\boldsymbol{\hat n}&=-\boldsymbol{A}_\tau \end{aligned} (n^×A)×n^A×n^×n^=Aτ=−Aτ
对于各向同性的线性介质,还可运用关系 E = 1 ε r D \boldsymbol{E}=\cfrac{1}{\varepsilon_r}\boldsymbol{D} E=εr1D 和 B = μ r H \boldsymbol{B}=\mu_r\boldsymbol{H} B=μrH 把涉及的 D , H \boldsymbol{D},\boldsymbol{H} D,H 改写成 E , B \boldsymbol{E},\boldsymbol{B} E,B 。
电规律和磁规律的对照
涉及到的事项:
- 自由电荷 ρ \rho ρ ,自由电流 J \boldsymbol{J} J (下标也记作f=free)
- 极化电荷 ρ b \rho_b ρb ,极化电流 J b \boldsymbol{J}_b Jb (下标b=bonding,也记作p=polarizated)
- 磁化电流 J m \boldsymbol{J}_m Jm (下标m=molecular,也记作m=magnetic)
Maxwell方程导出的守恒律
介质的极化和磁化会与外电磁场相互作用,所以讨论由介质和电磁场组成的整个体系的能量、动量等会十分复杂。以下讨论仅针对真空中的情况。具体地,该体系涉及电磁场的源——(自由)电荷密度分布和(自由)电流密度分布以及由它们在空间所产生的电磁场。
利用Maxwell方程推导守恒律的一般方法是,将表达式中的场源量 ρ , J \rho,\boldsymbol{J} ρ,J 用电磁场的时空微商替代。
电荷守恒定律
可以由 ( 1 ) , ( 2 ) (1),(2) (1),(2) ,或介质中的方程 ( 1 † ) , ( 2 † ) (1^\dagger),(2^\dagger) (1†),(2†) 推出。例如对 ( 2 ) (2) (2) 求散度并利用 ( 1 ) (1) (1) 就可以看到
∇ ⋅ ( ∇ × B − μ 0 ε 0 ∂ E ∂ t ) = − μ 0 ε 0 ∂ ∂ t ( ∇ ⋅ E ) = − μ 0 ∂ ρ ∂ t = μ 0 ∇ ⋅ J ∂ ρ ∂ t = − ∇ ⋅ J \begin{aligned} \nabla\cdot\left(\nabla\times\boldsymbol{B}-\mu_0\varepsilon_0\cfrac{\partial\boldsymbol{E}}{\partial t}\right)&=-\mu_0\varepsilon_0\cfrac{\partial}{\partial t}(\nabla\cdot\boldsymbol{E})=-\mu_0\cfrac{\partial\rho}{\partial t}=\mu_0\nabla\cdot\boldsymbol{J}\\ \frac{\partial\rho}{\partial t}&=-\nabla\cdot\boldsymbol{J} \end{aligned} ∇⋅(∇×B−μ0ε0∂t∂E)∂t∂ρ=−μ0ε0∂t∂(∇⋅E)=−μ0∂t∂ρ=μ0∇⋅J=−∇⋅J
也即电荷分布的连续方程。
能量守恒(Poynting’s Thm.)
电磁力对带电粒子 q q q 做功 q f ⋅ v = q ( E + v × B ) ⋅ v = q E ⋅ v q\boldsymbol{f}\cdot\boldsymbol{v}=q(E+\boldsymbol{v}\times\boldsymbol{B})\cdot\boldsymbol{v}=q\boldsymbol{E}\cdot\boldsymbol{v} qf⋅v=q(E+v×B)⋅v=qE⋅v 。对引起电流的(在体积中连续分布的)带电粒子,功率密度 w P = ρ E ⋅ v = J ⋅ E w_P=\rho\boldsymbol{E}\cdot\boldsymbol{v}=\boldsymbol{J}\cdot\boldsymbol{E} wP=ρE⋅v=J⋅E 。电磁场做的功转化为了带电粒子的机械能或热能。具体地:
P = ∫ V d τ ( J ⋅ E ) = ∫ V E ⋅ ( ∇ × H − ∂ D ∂ t ) d τ = ∫ V ( − ∇ ⋅ ( E × H ) − H ( ∇ × E ) − E ⋅ ∂ D ∂ t ) d τ = − ∫ V ( ∇ ⋅ ( E × H ) + H ∂ B ∂ t + E ∂ D ∂ t ) d τ \begin{aligned} P&=\int_V{\rm d}\tau(\boldsymbol{J}\cdot\boldsymbol{E})\\ &=\int_V\boldsymbol{E}\cdot\left(\nabla\times\boldsymbol{H}-\frac{\partial\boldsymbol{D}}{\partial t}\right){\rm d}\tau\\ &=\int_V\left(-\nabla\cdot(E\times H)-H(\nabla\times E)-E\cdot\frac{\partial D}{\partial t}\right){\rm d}\tau\\ &=-\int_V\left(\nabla\cdot(E\times H)+H\frac{\partial B}{\partial t}+E\frac{\partial D}{\partial t}\right){\rm d}\tau \end{aligned} P=∫Vdτ(J⋅E)=∫VE⋅(∇×H−∂t∂D)dτ=∫V(−∇⋅(E×H)−H(∇×E)−E⋅∂t∂D)dτ=−∫V(∇⋅(E×H)+H∂t∂B+E∂t∂D)dτ
根据上式的形式,定义电磁场的 能量密度 w = 1 2 ( E ⋅ D + B ⋅ H ) w=\cfrac12(\boldsymbol{E}\cdot\boldsymbol{D}+\boldsymbol{B}\cdot\boldsymbol{H}) w=21(E⋅D+B⋅H) 和 能流密度 S = E × H \boldsymbol{S}=\boldsymbol{E}\times\boldsymbol{H} S=E×H ,上式就写成了具有清晰物理意义的形式
∫ V ∂ w ∂ t d τ = − ∫ V ( ∇ ⋅ S + J ⋅ E ) d τ \int_V\frac{\partial w}{\partial t}{\rm d}\tau=-\int_V\left(\nabla\cdot\boldsymbol{S}+\boldsymbol{J}\cdot\boldsymbol{E}\right){\rm d}\tau ∫V∂t∂wdτ=−∫V(∇⋅S+J⋅E)dτ
这表明:电磁场能量的变化,等于 电磁场对荷电粒子做功 和 电磁场能流通过体积边界流出 的负值。
在真空中有 D = ε 0 E \boldsymbol{D}=\varepsilon_0\boldsymbol{E} D=ε0E 和 H = μ 0 − 1 B \boldsymbol{H}=\mu_0^{-1}\boldsymbol{B} H=μ0−1B ,于是又可以写出
u = 1 2 ε 0 E 2 + 1 2 μ 0 − 1 B 2 ≜ w e + w b S = μ 0 − 1 E × B \begin{aligned} u&=\frac12\varepsilon_0E^2+\frac12\mu_0^{-1}B^2\triangleq w_e+w_b\\ \boldsymbol{S}&=\mu_0^{-1}\boldsymbol{E}\times\boldsymbol{B} \end{aligned} uS=21ε0E2+21μ0−1B2≜we+wb=μ0−1E×B
动量守恒
记区域 V V V 内带电粒子(场源)的总动量为 p \boldsymbol{p} p ,则其变化量
d p d t = ∫ V ( ρ E + J × B ) d τ = ε 0 ∫ V ( ( ∇ ⋅ E ) E + B × ∂ E ∂ t − c 2 B × ( ∇ × B ) ) d τ = − ε 0 ∂ ∂ t ∫ V ( E × B ) d τ + ε 0 ∫ V ( ( ∇ ⋅ E ) E + E × ∂ B ∂ t − c 2 B × ( ∇ × B ) ) d τ = − ε 0 ∂ ∂ t ∫ V ( E × B ) d τ + ε 0 ∫ V ( ( ∇ ⋅ E ) E + ( ∇ × E ) × E ) d τ + μ 0 − 1 ∫ V ( ( ∇ ⋅ B ) B − ( ∇ × B ) × B ) d τ \begin{aligned} \frac{{\rm d}\boldsymbol{p}}{{\rm d}t}&=\int_V(\rho\boldsymbol{E}+\boldsymbol{J}\times\boldsymbol{B}){\rm d}\tau\\ &=\varepsilon_0\int_V\left((\nabla\cdot\boldsymbol{E})\boldsymbol{E}+\boldsymbol{B}\times\frac{\partial\boldsymbol{E}}{\partial t}-c^2\boldsymbol{B}\times(\nabla\times\boldsymbol{B})\right){\rm d}\tau\\ &=-\varepsilon_0\frac{\partial}{\partial t}\int_V(\boldsymbol{E}\times\boldsymbol{B}){\rm d}\tau +\varepsilon_0\int_V\left((\nabla\cdot\boldsymbol{E})\boldsymbol{E}+\boldsymbol{E}\times\frac{\partial\boldsymbol{B}}{\partial t}-c^2\boldsymbol{B}\times(\nabla\times\boldsymbol{B})\right){\rm d}\tau\\ &=-\varepsilon_0\frac{\partial}{\partial t}\int_V(\boldsymbol{E}\times\boldsymbol{B}){\rm d}\tau +\varepsilon_0\int_V\bigg((\nabla\cdot\boldsymbol{E})\boldsymbol{E}+(\nabla\times\boldsymbol{E})\times\boldsymbol{E}\bigg){\rm d}\tau+\mu_0^{-1}\int_V\bigg((\nabla\cdot\boldsymbol{B})\boldsymbol{B}-(\nabla\times\boldsymbol{B})\times\boldsymbol{B}\bigg){\rm d}\tau \end{aligned} dtdp=∫V(ρE+J×B)dτ=ε0∫V((∇⋅E)E+B×∂t∂E−c2B×(∇×B))dτ=−ε0∂t∂∫V(E×B)dτ+ε0∫V((∇⋅E)E+E×∂t∂B−c2B×(∇×B))dτ=−ε0∂t∂∫V(E×B)dτ+ε0∫V((∇⋅E)E+(∇×E)×E)dτ+μ0−1∫V((∇⋅B)B−(∇×B)×B)dτ
再利用恒等式
∇ ⋅ ( A A ) = ∂ i ( A i A j ) e ^ j = ( ∇ ⋅ A ) A + ( A ⋅ ∇ ) A ( ∇ × A ) × A = ( ∇ × A ) k ε k l m A l e ^ m = ( ∂ i A j ) ε i j k ε k l m A l e ^ m = e ^ j A i ∂ i A j − e ^ i A j ∂ j A j = ( A ⋅ ∇ ) A − 1 2 ∇ ( A 2 ) ∇ ( ψ I ⃗ ⃗ ) = e ^ i ∂ i ψ = ∇ ψ \begin{aligned} &\nabla\cdot(\boldsymbol{A}\boldsymbol{A})=\partial_i(A_iA_j)\boldsymbol{\hat e}_j=(\nabla\cdot\boldsymbol{A})\boldsymbol{A}+(\boldsymbol{A}\cdot\nabla)\boldsymbol{A}\\ &\begin{aligned} (\nabla\times\boldsymbol{A})\times\boldsymbol{A}&=(\nabla\times\boldsymbol{A})_k\varepsilon_{klm}A_l\boldsymbol{\hat e}_m=(\partial_iA_j)\varepsilon_{ijk}\varepsilon_{klm}A_l\boldsymbol{\hat e}_m\\ &=\boldsymbol{\hat e}_jA_i\partial_iA_j-\boldsymbol{\hat e}_iA_j\partial_jA_j\\ &=(\boldsymbol{A}\cdot\nabla)\boldsymbol{A}-\frac12\nabla(A^2) \end{aligned}\\ &\nabla(\psi\vec{\vec{I}})=\boldsymbol{\hat e}_i\partial_i\psi=\nabla\psi \end{aligned} ∇⋅(AA)=∂i(AiAj)e^j=(∇⋅A)A+(A⋅∇)A(∇×A)×A=(∇×A)kεklmAle^m=(∂iAj)εijkεklmAle^m=e^jAi∂iAj−e^iAj∂jAj=(A⋅∇)A−21∇(A2)∇(ψI)=e^i∂iψ=∇ψ
就有
( ∇ ⋅ A ) A + ( ∇ × A ) × A = ∇ ⋅ ( A A ) − 1 2 ∇ ( A 2 ) = ∇ ⋅ ( A A − 1 2 A 2 I ⃗ ⃗ ) (\nabla\cdot\boldsymbol{A})\boldsymbol{A}+(\nabla\times\boldsymbol{A})\times\boldsymbol{A}=\nabla\cdot(\boldsymbol{AA})-\cfrac12\nabla(A^2)=\nabla\cdot\left(\boldsymbol{AA}-\cfrac12A^2\vec{\vec{I}}\right) (∇⋅A)A+(∇×A)×A=∇⋅(AA)−21∇(A2)=∇⋅(AA−21A2I)
代入就有
d p d t + ε 0 d d t ∫ V ( E × B ) d τ = ε 0 ∫ V ( ∇ ⋅ ( E E ) − 1 2 ∇ ( E 2 ) ) d τ + μ 0 − 1 ∫ V ( ∇ ⋅ ( B B ) − 1 2 ∇ ( B 2 ) ) d τ \frac{{\rm d}\boldsymbol{p}}{{\rm d}t}+\varepsilon_0\frac{{\rm d}}{{\rm d}t}\int_V(\boldsymbol{E}\times\boldsymbol{B}){\rm d}\tau=\varepsilon_0\int_V\left(\nabla\cdot(\boldsymbol{EE})-\frac12\nabla(E^2)\right){\rm d}\tau+\mu_0^{-1}\int_V\left(\nabla\cdot(\boldsymbol{BB})-\frac12\nabla(B^2)\right){\rm d}\tau dtdp+ε0dtd∫V(E×B)dτ=ε0∫V(∇⋅(EE)−21∇(E2))dτ+μ0−1∫V(∇⋅(BB)−21∇(B2))dτ
其中
ρ E + J × B ≡ f = − ε 0 d d t ( E × B ) + ε 0 ∇ ⋅ ( E E − 1 2 E 2 I ⃗ ⃗ ) + μ 0 − 1 ∇ ⋅ ( B B − 1 2 B 2 I ⃗ ⃗ ) \rho\boldsymbol{E}+\boldsymbol{J}\times\boldsymbol{B}\equiv\boldsymbol{f}=-\varepsilon_0\frac{{\rm d}}{{\rm d}t}(\boldsymbol{E}\times\boldsymbol{B})+\varepsilon_0\nabla\cdot\left(\boldsymbol{EE}-\frac12E^2\vec{\vec{I}}\right)+\mu_0^{-1}\nabla\cdot\left(\boldsymbol{BB}-\frac12B^2\vec{\vec{I}}\right) ρE+J×B≡f=−ε0dtd(E×B)+ε0∇⋅(EE−21E2I)+μ0−1∇⋅(BB−21B2I)
再定义
-
上述 f \boldsymbol{f} f 是 洛伦兹力密度 ;
-
g = ε 0 E × B \boldsymbol{g}=\varepsilon_0\boldsymbol{E}\times\boldsymbol{B} g=ε0E×B 是 动量密度 ;
-
T ⃗ ⃗ = 1 2 ( ε 0 E 2 + μ 0 − 1 B 2 ) I ⃗ ⃗ − ε 0 E E − μ 0 − 1 B B \vec{\vec{T}}=\cfrac12\left(\varepsilon_0E^2+\mu_0^{-1}B^2\right)\vec{\vec{I}}-\varepsilon_0\boldsymbol{EE}-\mu_0^{-1}\boldsymbol{BB} T=21(ε0E2+μ0−1B2)I−ε0EE−μ0−1BB 是 动量流密度 。它是二阶对称张量,也叫 Maxwell应力张量 、 Maxwell协强张量 。
就得到了物理意义更加明显的形式
d p d t + d d t ∫ V g d τ = − ∫ V d τ ∇ ⋅ T ⃗ ⃗ = − ∮ ∂ V d S ⋅ T ⃗ ⃗ \begin{aligned} \frac{{\rm d}\boldsymbol{p}}{{\rm d}t}+\frac{{\rm d}}{{\rm d}t}\int_V\boldsymbol{g}{\rm d}\tau&= -\int_V{\rm d}\tau\nabla\cdot\vec{\vec{T}}\\ &=-\oint_{\partial V}{\rm d}\boldsymbol{S}\cdot\vec{\vec{T}} \end{aligned} dtdp+dtd∫Vgdτ=−∫Vdτ∇⋅T=−∮∂VdS⋅T
上式说明:任意区域内 带电粒子(场源)动量的变化率 d p d t \cfrac{{\rm d}\boldsymbol{p}}{{\rm d}t} dtdp 与该区域内 电磁场的动量变化率 d d t p f i e l d = d d t ∫ V g d τ \cfrac{{\rm d}}{{\rm d}t}\boldsymbol{p}_{field}=\cfrac{{\rm d}}{{\rm d}t}\int\limits_V\boldsymbol{g}{\rm d}\tau dtdpfield=dtdV∫gdτ 之和等于 通过该区域边界静流出的动量变化率 的负值。这里是把场中电荷、电流和电磁场场本身分开考虑的。
一般的动量守恒表达式可以写为 f = − d g d t − ∇ ⋅ T ⃗ ⃗ \boldsymbol{f}=-\cfrac{{\rm d}\boldsymbol{g}}{{\rm d}t}-\nabla\cdot\vec{\vec{T}} f=−dtdg−∇⋅T 。用于对荷电粒子施加电磁力的电磁场动量要么来自电磁场本身的动量,要么来自仅由区域边界的电磁场动量流入。
麦克斯韦协强张量写为 T ⃗ ⃗ = − ε 0 E E − μ 0 − 1 B B + ( ε 0 2 E 2 + 1 2 μ 0 B 2 ) I ⃗ ⃗ \vec{\vec{T}}=-\varepsilon_0\boldsymbol{EE}-\mu_0^{-1}\boldsymbol{BB}+\left(\cfrac{\varepsilon_0}{2}E^2+\cfrac{1}{2\mu_0}B^2\right)\vec{\vec{I}} T=−ε0EE−μ0−1BB+(2ε0E2+2μ01B2)I ,也被刘川老师记为
T ⃗ ⃗ = − ε 0 [ E i E j + c 2 B i B j − 1 2 ( E 2 + c 2 B 2 ) δ i j ] e ^ i e ^ j \vec{\vec{T}}=-\varepsilon_0\left[E_iE_j+c^{2}B_iB_j-\frac{1}{2}\left(E^2+c^2B^2\right)\delta_{ij}\right]\boldsymbol{\hat e}_i\boldsymbol{\hat e}_j T=−ε0[EiEj+c2BiBj−21(E2+c2B2)δij]e^ie^j
T ⃗ ⃗ \vec{\vec{T}} T 在边界面上的面积分体现了动量的流入。具体地,在空间任意曲面上某处取单位外法矢 n ^ \boldsymbol{\hat n} n^ ,那么 T i j n ^ j T_{ij}\hat{n}_j Tijn^j 等于通过该处单位面积、单位时间内流入动量的第 i i i 分量 p i p_i pi 。
还注意到,真空中电磁场动量密度和能流密度存在关系
g = ε 0 E × B = ε 0 μ 0 E × H = 1 c 2 S \boldsymbol{g}=\varepsilon_0\boldsymbol{E}\times\boldsymbol{B}=\varepsilon_0\mu_0\boldsymbol{E}\times\boldsymbol{H}=\cfrac{1}{c^2}\boldsymbol{S} g=ε0E×B=ε0μ0E×H=c21S
这并非偶然。
角动量守恒
关于守恒律的讨论
-
电磁场是客观存在的物质,而不仅是力线和场这些数学描述手段
电磁场自身具有能量、动量、角动量。电磁场通过与电荷和电流相互作用,可以进行能量、动量、角动量的交换和转化,而电荷、电流、电磁场整个体系的能量、动量、角动量守恒。只有考虑电磁场,这些守恒律才可以成立。这表明电磁场是客观的物理存在,相对法拉第的力线、场理论是巨大进步。 -
电磁场的守恒律是Maxwell方程和洛伦兹力方程的推论
-
牛顿第三定律问题
在静电和静磁问题中,两个孤立荷电粒子之间的作用满足牛顿第三定律;在场随时间变化的问题中,如果仍然只考虑这两个粒子,牛三不成立。考虑电磁场的动量后,守恒律成立。 -
光压
电磁波具有动量,所以光照在物体表面的时候会产生压强。
这篇关于一小时电动力学 02 麦克斯韦方程组的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









