游走专题

GNN-节点向量(Node Embedding)的表征学习-发展：随机游走/一阶二阶相似度(静态表征)【直接学习出各个节点的向量表示】 --＞图卷积(动态表征)【学习节点间聚合函数的参数】

静态表征基于“随机游走”、“Word2vec”的：DeepWalk、Node2vec、Metapath2vec；基于“一阶相似度”、“二阶相似度”的：LINE、SDNE；动态表征（GCN、GraphSAGE、GAT）【训练聚合函数的参数】

GNN-静态表征-随机游走-2014：DeepWalk【步骤：①随机游走策略生成每个节点的训练序列（DFS），得到训练数据集；②套用Word2vec算法得到节点表示】【捕获二阶相似度】【浅层、同质图】

一、概述 1、 2、DeepWalk、LINE、Node2vec对比提出的顺序DeepWalk 2014, UNE 2015, Node2Vec 2016 Node2Vec设置 p = q = 1 p=q =1

随机游走的PageRank算法 sensitive PageRank

随机游走的pagerank建立在pagerank基础之上， PageRank的简单介绍请看这里http://blog.csdn.net/zhonghuan1992/article/details/24396435 请先看随机游走的pageRank算法部分代码（代码写的挫了写见谅），根据代码分析 #include <cstdio>#include <cstring>#includ

数据包的游走

数据包在网络的游走：先从本地的路由开始找起，数据包到达路由时，路由会先对数据包进行解剖，然后通过其目的ip选择其在网络上的最优路径（这也就是所谓的路由功能了）。当其选择了所谓的最优路径之后，数据包同样也会产生相应的变化。一个数据包的结构中目的ip与源ip载整个传输过程中是不会改变的。但是其每当经过一个路由节点时数据包中的源mac与目的mac则会发生改变。打一个比方，我现在本机想googl

6.2.4 随机游走（Random Walk）

随机游走这一名称由Karl Pearson在1905年提出[Pearson, K. (1905). The problem of the Random Walk. Nature. 72, 294.]，本来是基于物理中"布朗运动"相关的微观粒子的运动形成的一个模型，后来这一模型作为数理金融中的重要的假设，指的是证券价格的时间序列将呈现随机状态，不会表现出某种可观测或统计的确定趋势，即证券价

1.8. 离散时间鞅-无界停时定理与随机游走

无界停时定理与随机游走无界停时定理与随机游走1. 无界停时定理1.1. 一致可积1.2. 非一致可积 2. 应用于随机游动-鞅方法2.1. 随机游走构造的鞅2.2. 对称简单随机游走无界停时定理与随机游走 1. 无界停时定理本节给出一致可积下鞅的无界停时定理,说明一致可积下鞅的停止过程一致可积,且满足 ( X N , F n (X

《经典论文阅读2》基于随机游走的节点表示学习—Deepwalk算法

word2vec使用语言天生具备序列这一特性训练得到词语的向量表示。而在图结构上，则存在无法序列的难题，因为图结构它不具备序列特性，就无法得到图节点的表示。deepwalk 的作者提出：可以使用在图上随机游走的方式得到一串序列，然后再根据得到游走序列进行node2vec的训练，进而获取得到图节点的表示。本质上deepwalk和word2vec师出同门（来自同一个思想），deepwalk算法的提出

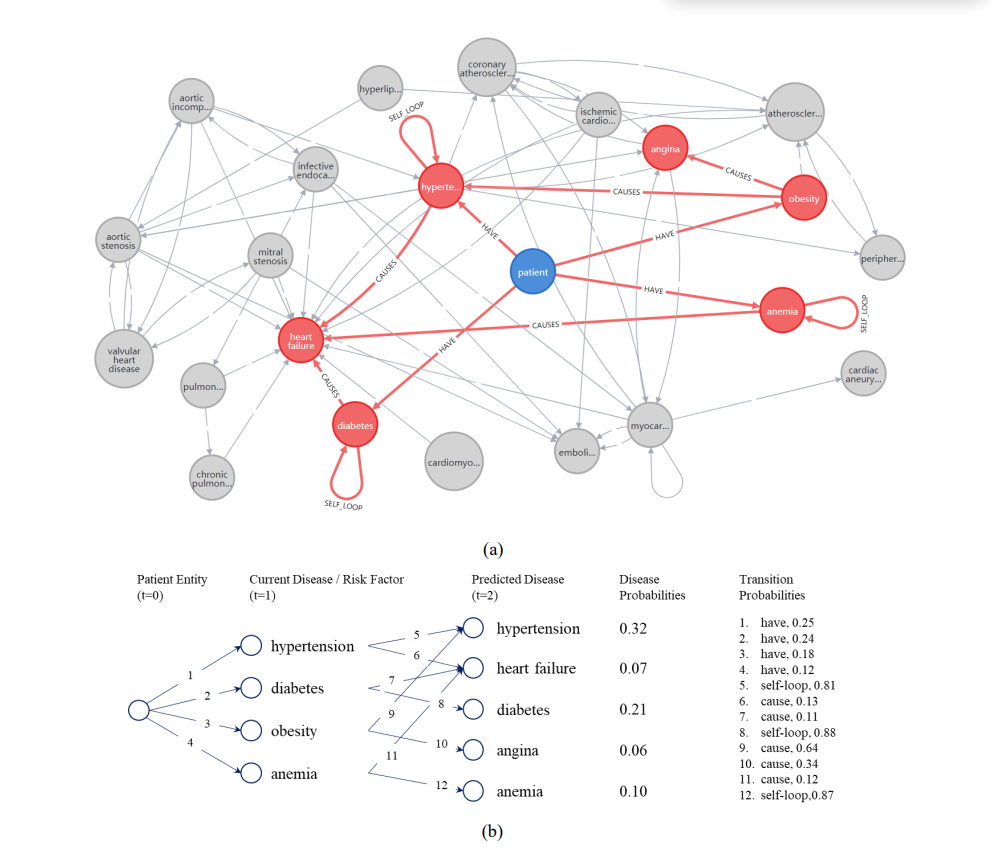
PBXAI：将疾病预测转为沿知识图谱的随机游走

PBXAI：将疾病预测转为沿知识图谱的随机游走 PBXAI = 知识图谱构建 + 病人特征与知识图谱连接 + 强化学习 + 疾病发展路径的生成PBXAI 流程PBXAI 算法设计论文： https://arxiv.org/ftp/arxiv/papers/2010/2010.08300.pdf 代码：https://github.com/ZJU-BMI/PBXAI

LOJ #2542 [PKUWC2018]随机游走 (概率期望、组合数学、子集和变换、Min-Max容斥)

很好很有趣很神仙的题！题目链接: https://loj.ac/problem/2542 题意: 请自行阅读题解首先我们显然要求的是几个随机变量的最大值的期望(不是期望的最大值)，然后这玩意很难求，根据Min-Max容斥化成最小值的期望来求。 Minn-max容斥是指\(\max(x_1,x_2,...,x_n)=\sum_{S\in \{1,2,...,n\} } (-1)^{|S|-1}

randomwalk随机游走

PageRank就是一种随机游走

游侠儿，游走大唐天空下

杨帆摇摇头，道：“不能一起走，皇帝命我护送公主，那这一路行程何时歇宿何时赶路、警戒安排、地方官接送等等一应事宜就该由我安排，我得抓紧时间。你有孕在身，不能颠簸，我让阿奴陪着你缓缓而行。” 　　对于杨帆和太平公主之间的那笔糊涂帐，小蛮多少也知道一些，她轻轻叹了口气，答应一声，没有再多说什么。她是个聪明的女子，知道丈夫心中有许多烦心事，不想多给他增加烦恼。　　杨帆握着她的手，轻轻笑道：“去了长

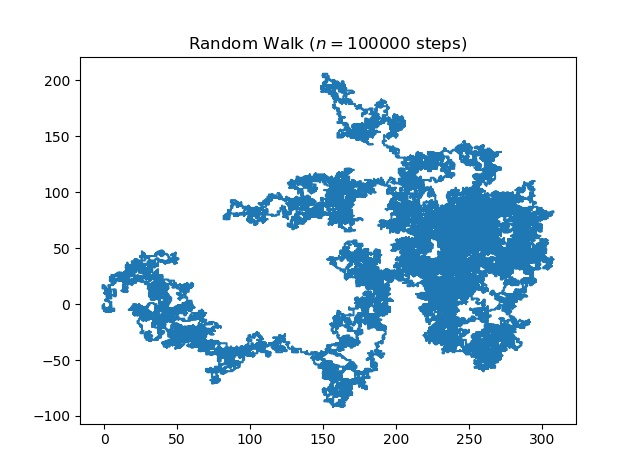
《Python编程：从入门到实践》中的随机游走实验

声明：代码来自《Python编程：从入门到实践》这本书，如有不当, 请联系作者SixAbs删除作者： SixAbs 摘要随机游走是随机过程里面的经典例子，今天在学习Python基础的时候看到这么个例子，觉得很直观形象，挺有意思。当然，看这个例子并不是本意，写这篇文章其实是先借助这么个例子，首先学习一下python的数据可视化的基础知识，其次是规范一下自己写博客的格式

NOIP 2021 第一题报数 number 游走在超时的边缘(不定长数组) 10分+30分+50分(纯暴力)+70分(约数范围缩到sqrt(x)之内 4倍2倍重复的筛法 )+100分(查找优化)

总目录详见：NOIP 提高组复赛试题目录信奥历年在线测评地址：洛谷 P7960 [NOIP2021] 报数 1.10分对于10% 的数据，T≤10，x≤100。纯暴力，极限情况，在x=100中傻傻找约数,1,2,3,......,99,100的方式，查找100次，再对约数进行判定，约数中数字是否含有7(极限是每个约数2次)，约数是否是7的倍数(极限是每个约数1次)，故此时对

P6154 游走

题意：给出有向无环图，可能存在重边，每条边的边权均为1，问从其中随机等可能的挑选一条路径，问挑选出边的长度的期望是多少思路：对于结果即为所有路径的长度总和除以总路径数量，而我们不容易直接找出所有路径然后计算长度总和，这题为有向无环图，所以我们可以通过拓扑来转移出以每个点为结尾的所所有路径的长度总和以及路径条数，正因为只有将所有一个点之前的所有点的状态全部得出之后，才能用这个点的状态来继续向下转

随机游走Python中的实现

随机游走是一个数学对象，称为随机或随机过程，它描述了一条路径，该路径由一些数学空间（如整数）上的一系列随机步骤组成。随机游走的一个基本例子是整数线上的随机游走，它从0开始，每一步以相等的概率移动+1或-1。其他例子包括分子在液体或气体中行进时的路径，觅食动物的搜索路径，波动股票的价格和赌徒的财务状况都可以通过随机行走模型来近似，即使它们在现实中可能不是真正的随机。如这些例子所示，随机游走在许多

人脸识别，游走在侵犯个人隐私的边缘

近日，一位购房者带着头盔去看房的新闻在网上迅速发酵，目前，80%以上售楼处安装了人脸识别系统。人脸识别一方面涉及个人隐私，另一方面涉及价格公正性，相关部门经过调查，要求售楼处撤除人脸识别系统。随着人脸识别系统的不断拓展，越来越多的行业领域运用人脸识别技术落地实践，与此同时，其存在的个人隐私问题也不容忽视。《杭州市物业管理条例（修订草案）》提请审议：禁止强制业主通过指纹、人脸识别

随机游走问题的神奇应用(一)

泊松方程的随机游走求解一.问题的提出二.问题的求解三.代码求解可以用monteCarlo方法构建一个随机游走过程来求解偏微分方程。一.问题的提出求解二维泊松方程的第一边值问题如下: ∂ 2 u ( P ) ∂ x + ∂ 2 u ( P ) ∂ y 2 = q ( P ) P ( x , y ) ∈ D \frac{\partial^2 u(P)}{\pa

带属性随机游走的图循环网络

1. 背景随机游走模型被广泛应用于从网络嵌入到标签传播的各种网络分析任务中。但是在真实的系统中，节点通常不是纯顶点，而是具有不同的特征。然而，为具有属性的网络开发随机游走模型是困难的，节点属性使得节点间的交互更加复杂，拓扑结构也更加异构。本文探索了在属性网络上进行联合随机游走，并利用它们来促进深度节点的学习。最后，利用实验与最先进的嵌入算法作比较，证明了模型的有效性。 2. 介绍

[HNOI2013]游走题解

[HNOI2013]游走 [HNOI2013]游走考虑每一条边的单独贡献，发现这个不是很好计算，而且边数其实很多。我们考虑对于一条 u → v u \to v u→v 的边，其贡献是 f ( u ) d e g ( u ) + f ( v ) d e g ( v ) \dfrac{f(u)}{deg(u)} + \dfrac{f(v)}{deg(v)} deg(u)f(u)

[转]数轴上的随机游走问题

数轴原点上有一个点，每步以1/2的概率向左或向右移动1个单位长度（下文称为一步随机游走），由此可以引出许多有趣的问题：随机游走n步后距原点距离的期望对这个问题可以分情况讨论：n为奇数或n为偶数。当n为奇数时，设n=2k+1，k为非负整数，由于正反方向是对称的，下面考虑这个点坐标为正的情况：设点向正方向上走了n-i步，负方向上走了i步，i=0,1,2,...,k，则

CS224W3.2——随机游走（Random Walk）

上一文中说道定义节点相似度函数的时候使用Random Walk方法： CS224W3.1——节点Embedding 这节课来说一下Random Walk方法。在这篇中，我们来看一个更有效的相似函数——在图上随机游走的节点共现的概率。我们介绍随机游走背后的直觉，我们将优化的目标函数，以及我们如何有效地执行优化。我们引入了node2vec，它结合了BFS和DFS来推广随机游走的概念。文章

游走在合法与非法边缘网约护士会是一个不错的共享经济项目吗？

网约护士在国内并不算一个新概念，其实它在国内的兴起还是有一定“历史”。早在2015年，上海就出现了市场主导的“网约护士”，虽说当时app没什么名气，但在当地也实现了一天过万的服务。也许在那个时候，市场还是为网约护士埋下了发展潜力。 2月12日，国家卫健委发布《“互联网+护理服务”试点工作方案》，确定北京市、天津市、上海市、江苏省、浙江省、广东省作为“互联网+护理服务”试点省份并开展相关试点工作

领略魅力：论坛文章采集器带你游走互联网

作为一名热衷于网络信息的探索者，我不禁想到了一个有趣的话题：论坛文章采集器。作为一个高效获取知识和信息的工具，论坛文章采集器在当今社会发挥着重要的作用。下面，我将从多个维度来探讨这一话题，带你一起领略论坛文章采集器的魅力。 1.提供海量精华内容论坛文章采集器不仅可以帮助用户自动搜索和收集各类优质文章，还能根据用户的需求进行智能推荐。无论你是对科技、娱乐、健康还是其他领域感兴趣，论坛文章采集器

把「醉汉游走」引入「三体问题」，以色列学者新思路登上物理学顶刊

来源：机器之心编辑：nhyilin 两位以色列物理学者采用了名为「醉汉游走」的随机游走模式，为「三体问题」引入了新思路。当牛顿第一次发现两个物体之间通过引力相互作用时，他就已经破解了物质在广阔时空中移动和相互作用的密码。然而这一发现是关于两个物体之间的相互作用，三个相互环绕的物体之间的相互作用，即「三体问题」，牛顿并未解决。距离牛顿提出「三体问题」已经过去了三个世纪，但一直没有人能够解决

第0章随机游走——《processing》学习，自己完成实验的代码

1.第一个的尝试：完整代码如下： //主函数代码Walker[] w;int total = 0;void setup() {frameRate(30);size(600, 400);w = new Walker[20];for (int i = 0; i < w.length; i++) {w[i] = new Walker();}}void draw() {background(25

树上游走最优策略问题：Cf1725J

https://codeforces.com/contest/1725/problem/J 首先要转化题目发现题目本质是什么不用回去 = 少走一条路径传送 = 少走另一条路径一开始猜的结论是这样但这并不完整传送本质是让我们把某些路径少走一遍考虑这种情况，交于1点 #include<bits/stdc++.h>using namespace std;#def