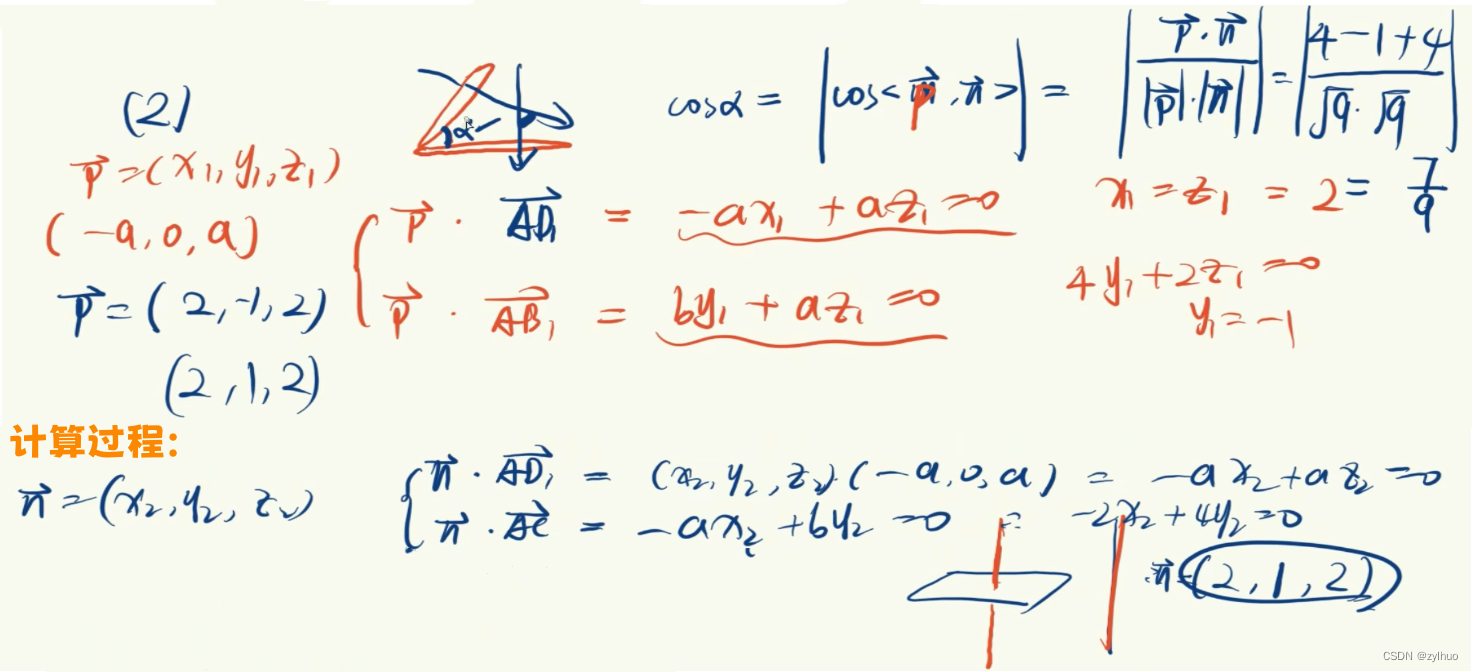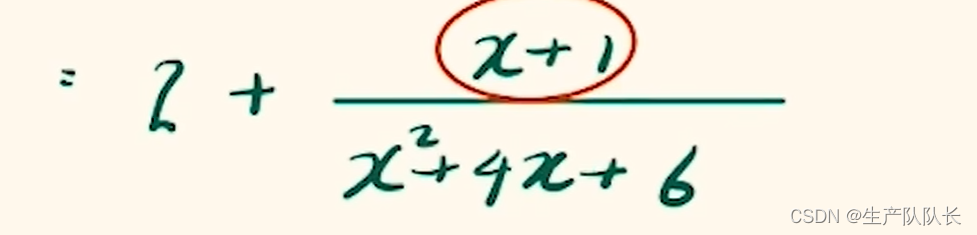求法专题
Java中的八种基本数据类型所占字节的求法
Java中有八种基本数据类型,分别为:byte、short、int、long、float、double、char、boolean。 这八种基本类型都有对应的包装类,分别为:Byte、Short、Integer、Long、Float、Double、Character、Boolean。 面试时时常会闻到这八种基本类型及其包装类,而且各种基本类型所占的字节数即使记不住、能用代码实现也
day03 负数二进制求法
字符类型名称是char 字符类型里包含256个不同的整数,每个 整数可以用来代表一个字符(例如'a', '^'等) 这些整数和字符可以互相替代 ASCII码表中列出所有整数和字符的对应关系 'a' 97 'A' 65 '0' 48 ASCII码表里所有小写英文字母是连续排列的, 并且'a'对应的整数最小,字母'z'对应的
一个求公约数和公倍数的有趣求法
代码: #include<stdio.h> #include<algorithm> using namespace std; int gcd(int x, int y) { while(x^=y^=x^=y%=x); return y; } int f(int x, int y) { return x * y / gcd(x, y); } int main() { int
阿里云oss Multipart Upload 中每个part的E-tag(即MD5)求法
阿里云java的开发文档中提到:OSS 会将服务器端收到 Part 数据的 MD5 值放在 ETag 头内返回给用户。 为了保证数据在网络传输过程中不出现错误,强烈推荐用户在收到 OSS 的返回请求后,用该 MD5 值验证上传数据的正确性。 但是没有告诉怎么验证,纠结了一天之后终于找到了在本地求每个part的MD5值得方法: <span style="font-size:18
AI-数学-高中-40法向量求法
原作者视频:【空间向量】【考点精华】3法向量求法稳固(基础)_哔哩哔哩_bilibili 注意:法向量对长度没有限制,求法向量时,可以假设法向量z为任意一个取非0的值。 示例1: 示例2:
概率论 —— 相关分布以及期望方差的求法汇总
离散型 1. 两点分布(伯努利分布) 在一次试验中,事bai件A出现的概du率为P,事件A不出现的概率为q=l -p,若以X记一次试zhi验中A出现的次数,则X仅取0、I两个值。 两点分布是试验次数为1的伯努利试验。 2. 二项分布 是重复n次独立的伯努利试验。在每次试验中只有两种可能的结果,而且两种结果发生与否互相对立,并且相互独立,与其它各次试验结果无关,事件发生与否的概率在每一次独立试
2020牛客暑期多校训练营(第九场)C Groundhog and Gaming Time —— 期望+线段树,长度平方期望的求法,有丶东西
This way 题意: 现在有n个线段,每个线段有1/2的可能会被选中,问你被选中的这些线段的交集的长度的平方的期望是多少。 题解: 对于求这种期望我是一窍不通,理解别人的代码也理解了好久才恍恍惚惚好像知道了的样子,难受 首先我们可以将所有的线段分成一个一个小段,然后去做每个小段的贡献: 比如说这三个黑色线段我们就可以将他们分成一个一个红色的小段。 然后对于每一个小段p的贡献: 假设
POJ 3070 Fibonacci (矩阵快速幂 Fibonacci数列新求法)
Fibonacci Time Limit: 1000MS Memory Limit: 65536KTotal Submissions: 9974 Accepted: 7115 Description In the Fibonacci integer sequence, F0 = 0, F1 = 1, and Fn = Fn − 1 + Fn − 2 for n ≥
最短路径的求法(SPFA,dijkstra)
关于SPFA 算法大致流程是用一个队列来进行维护。 初始时将源加入队列。 每次从队列中取出一个元素,并对所有与他相邻的点进行松弛,若某个相邻的点松弛成功, 如果该点没有在队列中,则将其入队。 直到队列为空时算法结束。 判断有无负环:如果某个点进入队列的次数超过V次则存在负环 代码 #include<bits/stdc++.h>using namespace std;const in
n介导plus!,高阶导数求法又增加了
我曾经的n介导的经历 上面是我曾经在n介导求导的一个例子,如今呢,我又碰到了相关了列题,也是求n介导,其中的方法也是我曾经有印象的,但很可惜,当初还没接触csdn,没在上面记下来。 现在呢,该记下来了 上题目:,求n介导 有两种方法可以解决它 第一种,也是我一开始记得这种方法,可惜随着时间的流逝,历年考试也没怎么考到,有点淡忘这种方法了,还好如今碰到这道题了,让我想起来了。
高中数学:分式函数值域的求法
一、求值域的两种基本思路 1、根据函数图像和定义域求出值域。 难点:画出函数图像 2、研究函数单调性和定义域求出值域。 本篇主要讲一下,画图法求值域 二、函数图像画法 高中所学的分式函数,基本由反比例函数平移得到。 复杂分式函数图像画法的两个要点: a、找垂直、水平渐近线 垂直渐近线:分母等于0时,x的取值水平渐近线:x取无穷大的时候,y的极限值 b、代值定象限 当你不确定图像
c、c++关于质数||素数的求法
我们要求某个范围内的所有质数,当然最基本最重要的方法就是除一个数取余数在判断是否为0 一、最简单的粗暴的穷举法 #include<iostream>#include<math.h>#include<time.h>#define max 100using namespace std;void main() {clock_t start, end;start = clock();int
线性代数----逆矩阵的性质和求法
##逆矩阵的性质和求法 逆矩阵的性质 性质1: A 可 逆 ⇒ ∣ A − 1 ∣ = 1 ∣ A ∣ A可逆\Rightarrow|A^{-1}| = \frac{1}{|A|} A可逆⇒∣A−1∣=∣A∣1 性质2: A 可 逆 ⇒ A − 1 可 逆 , ( A − 1 ) − 1 = A A可逆\Rightarrow A^{-1}可逆, (A^{-1})^{-1}=A A可逆⇒
逆元相关知识点、求法(快速幂,拓展欧几里得,线性算法,阶乘的逆元)及拓展欧几里得算法的应用
概念: 若xy≡1 (mod p),且gcd(x,p)=1(gcd函数是求x,y的最大公约数),则称x关于模p的乘法逆元为y。 那么除以y相当于乘以x(模p情况下)。值得注意的是x(y+k*p)≡1(mod p),逆元不止一个,求最小的就可以; 几个定理or算法: 1.费马小定理:x^(p-1) ≡1 (mod p),p为素数,x不为p的倍数,若x为p的倍数则x^p ≡p (mod p)。那
刚学习的最长不递增子序列的新求法
P1020 [NOIP1999 提高组] 导弹拦截 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 在做这题的时候学到的 我看说是复杂度在O(nlogn)的算法才能通过这题 普通的办法就不行了(之前写过) 然后我去看题解,学了这种新的方法 网址如下:题解 P1020 【[NOIP1999 普及组] 导弹拦截】 - 古明地觉世界第一! - 洛谷博客 (luogu.com.
斐波那契数列的各种求法
斐波那契数列百科名片 “斐波那契数列”是意大利数学家列昂纳多·斐波那契首先研究的一种递归数列, 它的每一项都等于前两项之和。 此数列的前几项为1,1,2,3,5等等。 在生物数学中,许多生物现象都会呈现出斐波那契数列的规律。斐波那契数列相邻两项的比值趋近于黄金分割数。此外,斐波那契数也以密码的方式出现在诸如《达芬奇密码》的影视书籍中。 目录[隐藏] 【奇妙的属性】 【影视链接】 【相关的数学问题
二叉树前序、中序、后序遍历相互求法(实例)
1.已知先序和中序求后序 先序遍历的节点顺序是:ADCEFGHB,中序遍历是CDFEGHAB,则后序遍历的结果是 CFHGEDBA 解:1)根据先序遍历结果可知A是根节点,根据中序遍历知道A的左子树是(CDFEGH),右子树是(B) 2)左边中D是根节点,由中序遍历的顺序CD知道,C是D的左子树; E是D的右子树,由中序遍历的顺序FE知道,F是E的左子树;
二叉树前序、中序、后序遍历相互求法 (原理,程序)
今天来总结下二叉树前序、中序、后序遍历相互求法,即如果知道两个的遍历,如何求第三种遍历方法,比较笨的方法是画出来二叉树,然后根据各种遍历不同的特性来求,也可以编程求出,下面我们分别说明。 首先,我们看看前序、中序、后序遍历的特性: 前序遍历: 1.访问根节点 2.前序遍历左子树 3.前序遍历右子树 中序遍历: 1.中序遍历左子树
一看就会的判断链表中是否有环求法
判断链表中是否有环 题目描述: 判断给定的链表中是否有环。如果有环则返回true,否则返回false。 你能给出空间复杂度的解法么? 输入分为2部分,第一部分为链表,第二部分代表是否有环,然后回组成head头结点传入到函数里面。-1代表无环,其他的数字代表有环,这些参数解释仅仅是为了方便读者自测调试 示例: 输入:{3,2,0,-4},1 返回值:true 说明:第一部分{3,2,0,-4
数据库最小函数依赖求法 附相关习题及解析
首先我们给出最小函数依赖的定义 如果函数依赖集F满足下列条件,则称F为最小函数依赖集或最小覆盖。 ① F中的任何一个函数依赖的右部仅含有一个属性; ② F中不存在这样一个函数依赖X→A,使得F与F-{X→A}等价; ③ F中不存在这样一个函数依赖X→A,X有真子集Z使得F-{X→A}∪{Z→A}与F等价。 可能我们大多数开始看的时候,都会觉得的很绕口,其实很简单,就是有一些字母 X 和函数依赖
数据库闭包求法 附相关习题及解析
闭包就是由一个属性直接或间接推导出的所有属性的集合 以下是写的比较科学规范的闭包求解方法,设X和Y均为关系R的属性集的子集,F是R上的函数依赖集,若对R的任一属性集B,一旦X→B,必有B⊆Y,且对R的任一满足以上条件的属性集Y1 ,必有Y⊆Y1,此时称Y为属性集X在函数依赖集F下的闭包,记作X+。 计算关系R的属性集X的闭包的步骤如下: 第一步:设最终将成为闭包的属性集是Y,把Y初始化为X;
欧拉函数的求法(线性筛法?)
include<bits/stdc++.h> using namespace std; typedef long long ll; ll phi[100001]; const int N=100000; void init() { for ( int i=1;i<=N;i++) phi[i]=i;
UVA 11186 - Circum Triangle(圆上三角形求法)
这个题 感觉数据是500 就直接三层循环上去了。 。但是超时了。 我用了最简单的方法 可能是运算量略大的原因吧。(好吧。 在自己稍微优化之后A了。 跑了2.059秒,代码在最后面) 在不会优化的情况下。 去网上搜了题解。 第一份代码。 在我看明白之后 不得不佩服 原作者的聪明机智。 也算是 学到了。 先上代码后讲解。 #include <cs