梁友栋专题
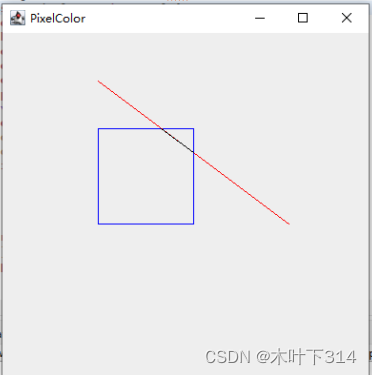
OpenGL梁友栋-Barsky算法裁剪线段
使用C++语言 裁剪线段P1(3,3),P2(-2,-1),裁剪窗口为wxl=0,wxr=2,wyb=0,wyt=2。 // 梁友栋-barsky算法.cpp : 定义控制台应用程序的入口点。//#include "stdafx.h"#include <GL/glut.h>#include <iostream>#include <cmath>#include <algorithm>d
光栅图形学(三)——梁友栋-Barskey剪裁算法
光栅图形学(三)——梁友栋-Barskey剪裁算法 一、问题转换 直线的参数方程 x = x 1 + u ( x 2 − x 1 ) y = y 1 + u ( y 2 − y 1 ) \begin{aligned} &x = x_1+u(x_2-x_1) \\ &y=y_1+ u(y_2-y_1) \end{aligned} x=x1+u(x2−x1)y=y1+u
C语言实现梁友栋-Barsky算法
前言: (引用梁友栋-Barsky裁剪算法_梁友栋 barsky算法-CSDN博客) Cyrus和Beck用参数化方法提出了比Cohen-Sutherland更有效的算法。后来梁友栋和Barsky独立地提出了更快的参数化线段裁剪算法,也称为Liany-Barsky(LB)算法。 一、梁友栋-Barsky裁剪算法思想: 我们知道,一条两端点为P1(x1,y1)、P2(x2,y2
计算机图像学实验-Cyrus-Beck算法和梁友栋-Barsky算法(java实现附代码)
实验内容 1、用Cyrus-Beck算法进行给定直线的裁剪 2、用梁友栋-Barsky算法进行给定直线的裁剪 实验代码 1、用Cyrus-Beck算法进行给定直线的裁剪 //Cyrus-Beck算法import java.awt.*;import java.applet.Applet;public class CyrusBeck extends Applet{double ts
梁友栋-Barsky裁剪算法
Cyrus和Beck用参数化方法提出了比Cohen-Sutherland更有效的算法。后来梁友栋和Barsky独立地提出了更快的参数化线段裁剪算法,也称为Liany-Barsky(LB)算法。 一、梁友栋-Barsky裁剪算法思想: 我们知道,一条两端点为P1(x1,y1)、P2(x2,y2)的线段可以用参数方程形式表示: x= x1+ u·(x2-x1)= x1+