计算机图像学实验-Cyrus-Beck算法和梁友栋-Barsky算法（java实现附代码）

实验内容

1、用Cyrus-Beck算法进行给定直线的裁剪 

2、用梁友栋-Barsky算法进行给定直线的裁剪

实验代码

1、用Cyrus-Beck算法进行给定直线的裁剪

//Cyrus-Beck算法
import java.awt.*;
import java.applet.Applet;
public class CyrusBeck extends Applet{double ts = 0, te = 1;public void paint(Graphics g) {// 绘制裁剪窗口g.setColor(Color.pink);int[] xPoints = {200, 84, 318};int[] yPoints = {275, 100, 100};g.drawPolygon(xPoints, yPoints, 3);// 绘制被裁剪直线g.setColor(Color.blue);g.drawLine(0, 120, 400, 120);g.drawLine(0, 180, 400, 180);// 进行裁剪double[][] A = {{200, 275}, {84+1/3, 100}, {318+2/3, 100}};// 计算法向量数组Ndouble[][] N = new double[3][2];for (int i = 0; i < 3; i++) {int next = (i + 1) % 3;double dx = A[next][0] - A[i][0];double dy = A[next][1] - A[i][1];N[i][0] = -dy;N[i][1] = dx;}double[] x = {0, 400};double[] y1 = {120, 120};double[] y2 = {180, 180};g.setColor(Color.orange);Cyrus_Beck(g, A, N, x, y1, ts, te);g.setColor(Color.black);Cyrus_Beck(g, A, N, x, y2, ts, te);}public void Cyrus_Beck(Graphics g, double[][] A, double[][] N, double[] x, double[] y, double ts, double te) {boolean draw = true;int i;double t, dn, nw;for (i = 0; i < 3; i++) {dn = N[i][0] * (x[1] - x[0]) + N[i][1] * (y[1] - y[0]);nw = N[i][0] * (x[0] - A[i][0]) + N[i][1] * (y[0] - A[i][1]);t = -nw / dn;if (dn < 0) {if (t < te) te = t;} else if (t > ts) ts = t;if (ts > te) draw = false;}if (draw) {double xs = (x[1] - x[0]) * ts + x[0];double ys = (y[1] - y[0]) * ts + y[0];double xe = (x[1] - x[0]) * te + x[0];double ye = (y[1] - y[0]) * te + y[0];g.drawLine((int) xs, (int) ys, (int) xe, (int) ye);}
}
}

 2、用梁友栋-Barsky算法进行给定直线的裁剪

//梁友栋-Barsky算法
import javax.swing.*;//引入swing包
import java.awt.*;//引入图形软件包awt
class Liang_Barsky extends JPanel {double xL = 100, xR = 200, yT = 200, yB = 100;    //矩形的边所对应的两个x，y坐标boolean visible;double[] x = {100, 300};double[] y = {50, 200};double ts = 0, te = 1;public boolean Liang_Barsky(double[] x, double[] y) {visible = false;double dx, dy;dx = x[1] - x[0];dy = y[1] - y[0];if (clipt(-dx, x[0] - xL))if (clipt(dx, xR - x[0]))if (clipt(-dy, y[0] - yB))if (clipt(dy, yT - y[0]))visible = true;return visible;}public boolean clipt(double r, double s) {double t;this.ts=ts;this.te=te;if (r < 0) {t = s / r;if (t > te) return false;else if (t > ts) ts = t;} else if (r > 0) {t = s / r;if (t < ts) return false;else if (t < te) te = t;} else if (s < 0) return false;return true;}public void paintComponent(Graphics g) {g.setColor(Color.blue); 							//设置绘图颜色drawLine(g, (int) xL, (int) yT, (int) xL, (int) yB);//绘制裁剪窗口drawLine(g, (int) xL, (int) yT, (int) xR, (int) yT);drawLine(g, (int) xL, (int) yB, (int) xR, (int) yB);drawLine(g, (int) xR, (int) yT, (int) xR, (int) yB);g.setColor(Color.red); 								//设置绘图颜色drawLine(g, (int) x[0], (int) y[0], (int) x[1], (int) y[1]);//绘制裁剪前直线if (Liang_Barsky(x, y)) {g.setColor(Color.black); 						//设置绘图颜色double x1 = x[0] + ts * (x[1] - x[0]);double y1 = y[0] + ts * (y[1] - y[0]);double x2 = x[0] + te * (x[1] - x[0]);double y2 = y[0] + te * (y[1] - y[0]);drawLine(g, (int) x1, (int) y1, (int) x2, (int) y2);//绘制裁剪后直线}}void drawLine(Graphics g, int x1, int y1, int x2, int y2) {g.drawLine(x1, y1, x2, y2);}
}

运行结果

1、Cyrus-Beck算法运行结果

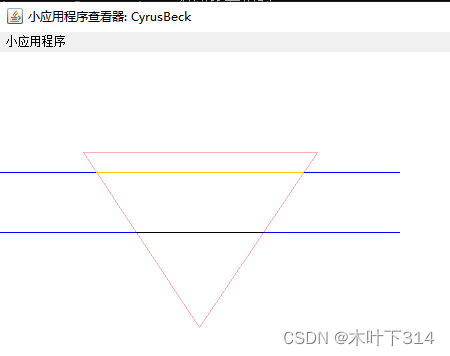
2、梁友栋-Barsky算法运行结果

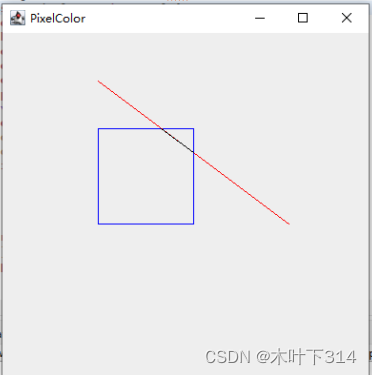
        梁友栋-Barsky裁减算法，过几天补充！

        梁友栋-Barsky裁减算法已补充。//2023.6.2