格点专题
Echarts3.0加载和订正气象格点数据源码
源码 function getValues(){var type = "TMP";var apoint = arguments[4] ? arguments[4] : 20;// 设置参数point的默认值为20var pdata = {"point" : apoint}; $.ajax({type : "post",async : true, //异步请求(同步请求将会锁
Echarts3.0加载和订正气象格点数据
前言 主要是对气象格点数据的主观订正,分为两个方面:运用ajax调用接口数据;echarts3.0展示及修改数据。修改后的保存没有涉及,接口的制作没有。 ajax调用数据 function getValues(){var type = "TMP";//取温度var apoint = arguments[4] ? arguments[4] : 20;// 设置参数point的默认值为20var
(ssl 2348)连接格点#kruskal,并查集#
题目 有一个 M M M行 N N N列的点阵,相邻两点可以相连。一条纵向的连线花费一个单位,一条横向的连线花费两个单位。某些点之间已经有连线了,试问至少还需要花费多少个单位才能使所有的点全部连通。 分析 容我解释测试点 所以,既然求最小生成树,纵向优先。 那怎样连呢,Kruskal 首先一件重要的事情就是并查集是一维的。 所以 ( x , y ) (x,y) (x,y)用 ( x − 1
python气象数据处理--按照时间序列计算格点数据指标
python气象数据处理–按照时间序列计算格点数据指标 聚合分类分析 python气象数据处理--按照时间序列计算格点数据指标前言一、以hourly数据为例二、使用步骤1.引入库并读取数据2.处理指标 总结 前言 气象数据常常以netcdf的形式存储,通常以hourly、daily、monthly、yearly等时间精度存储,但是我们常常需要处理成月、年、季节、气候态等
中国天然径流量格点数据集CNRD v1.0(1961-2018)
简介 中国天然径流量是指在中国境内自然形成的各种河流、湖泊、水库等水体中自然产生的流量。根据中国水利部的数据,中国天然径流量在年际变化和地区分布上都非常不均衡。北方地区径流量较小,南方地区则较大;而东部沿海地区的水资源较为丰富,而西北干旱地区的水资源则非常匮乏。此外,中国的天然径流量受气候变化、人类活动等因素的影响也非常大。前言 – 人工智能教程 格点数据集CNRD v1.0(1961-201
中国天然径流量格点数据集CNRD v1.0(1961-2018)
简介 中国天然径流量是指在中国境内自然形成的各种河流、湖泊、水库等水体中自然产生的流量。根据中国水利部的数据,中国天然径流量在年际变化和地区分布上都非常不均衡。北方地区径流量较小,南方地区则较大;而东部沿海地区的水资源较为丰富,而西北干旱地区的水资源则非常匮乏。此外,中国的天然径流量受气候变化、人类活动等因素的影响也非常大。前言 – 人工智能教程 格点数据集CNRD v1.0(1961-201
2020寒假牛客第一场——A honoka和格点三角形
示例1 思路: x方向有m格点,y方向n个格点 面积为1的三角形有两种情况:底2高1,底1高2 第一种情况:底2高1 (1)平行x轴:最下面一行开始,每一行有(m-2)个长为2的线段,上面一行对应m个格点全部可以连成三角形,一共(n-1)行,从最上面开始同理,所以共:2*(m-2)m(n-1) (2)平行y轴:同上,m,n交换位置:2*(n-2)n(m-1) 第二种情况:底1高2 因为直角三角形的
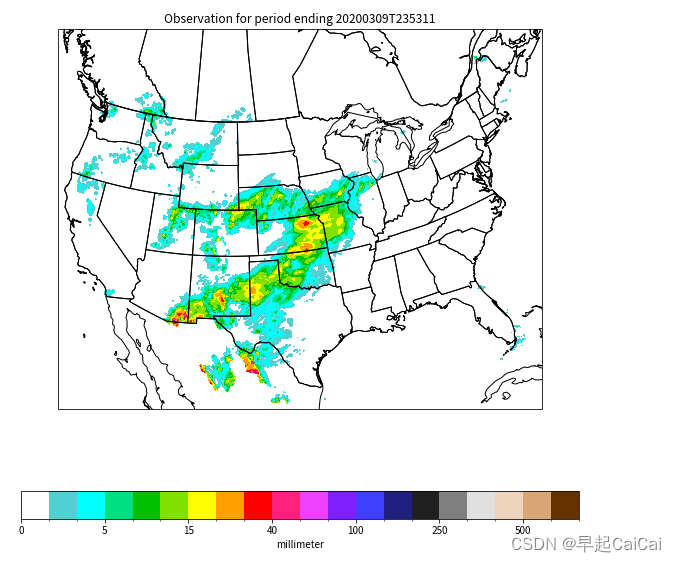
格点数据可视化(美国站点的日降雨数据)
获取美国站点的日降雨量的格点数据,并且可视化 导入模块 from datetime import datetime, timedeltafrom urllib.request import urlopenimport cartopy.crs as ccrsimport cartopy.feature as cfeatureimport matplotlib.colors as mcol