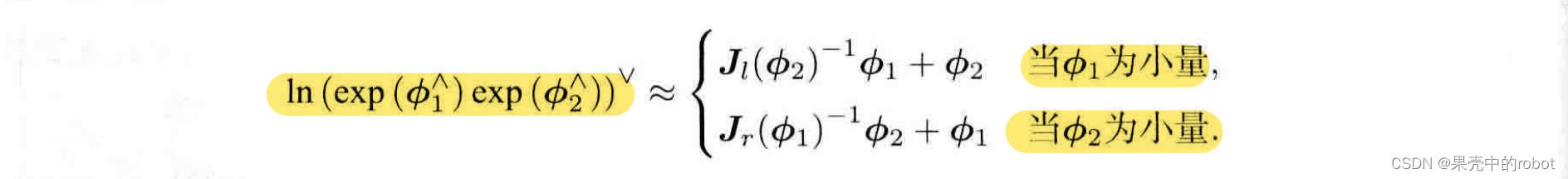李群专题
解读《视觉SLAM十四讲》,带你一步一步入门视觉SLAM—— 第 4 讲 李群与李代数 (下)
在上一篇解读中《解读《视觉SLAM十四讲》,带你一步一步入门视觉SLAM—— 第 4 讲 李群与李代数 (上)》,我们先介绍了李群的定义,知道了我们前面介绍的旋转矩阵集合就是一个李群,然后我们通过一些推导得到了 R = e x p ( ϕ ∧ ) R = exp(\boldsymbol\phi^{\wedge}) R=exp(ϕ∧),知道了旋转矩阵可以用李代数(向量)的形式去表示。 这一
半闲居士视觉SLAM十四讲笔记(4)李群与李代数 - part 2 指数与对数映射、李代数求导与扰动模型
本系列文章由 youngpan1101 出品,转载请注明出处。 文章链接: http://blog.csdn.net/youngpan1101/article/details/71087919 作者:宋洋鹏(youngpan1101) 邮箱: yangpeng_song@163.com 该讲详细资料下载链接 【Baidu Yun】【Video】【Code】 若您觉得本博文对您有帮
李群与李代数1:对应关系及指数/对数映射
李群与李代数1:对应关系及指数/对数映射 1. 群和李群1.1 群的引出1.2 群和李群定义及性质 2. 由李群引出李代数2.1 反对称矩阵对应向量与求导关系2.2 一阶导数矩阵求解 3. 李代数3.1 李代数的定义3.2 李代数 s o ( 3 ) \mathfrak{so}(3) so(3)3.3 李代数 s e ( 3 ) \mathfrak{se}(3) se(3) 4. 指数和对数
【李群李代数】【manif 】基于固定信标的2D机器人定位 (Error State Kalman Filter)...
demo演示 运行结果 我们考虑一个机器人在平面上被少量的准时地标或_信标 包围。 机器人以轴向速度和角速度的形式接收控制动作,并且能够测量信标相对于其自身参考系的位置。 机器人位姿 X 在 SE(2) 中,信标位置 b_k 在 R^2 中, | cos th -sin th x | * X = | sin th cos th y | //位置和方向
《第4讲 李群和李代数 》读书笔记
本文是《视觉SLAM十四讲》第4讲的个人读书笔记,为防止后期记忆遗忘写的。 本节目标 总结李群与李代数的概念,知道为什么要引出它们。掌握 SO(3), SE(3) 与对应李代数的表示方式。回忆 BCH 公式以及近似的意义。总结在李代数上的扰动模型。使用 Sophus 对李代数进行运算。 这一节的知识点串联思路 在 SLAM 中,除了表示位姿之外,我们还要对它们进行估计和优化。因为在 S
视觉slam十四讲:4.李群和李代数(包含实践部分)
目录 0.前言: 1.李群和李代数 1.1群的定义 1.1.1李群SO3、SE3 1.2李代数的引出 1.3李代数的定义 1.3.1李代数so3 1.3.2李代数se3 2.指数与对数映射 2.1SO3上的指数映射 2.1.1指数映射的性质: 2.2SE3上的指数映射 3.李群、李代数的定义与相互的转换关系 4.李代数求导与扰动模型 4.1BCH公
第4讲 李群与李代数-部分习题解答
5.证明: R p ∧ R T = ( R p ) ∧ . Rp^{\wedge }R^{T} = (Rp)^{\wedge}. Rp∧RT=(Rp)∧. 证明: ⇒ ( R p ) ∧ n = ( R p ) × ( R R − 1 n ) = R [ p × ( R − 1 n ) ] = R p ∧ R ⊤ n \Rightarrow (Rp)^{\wedge}n = (Rp) \ti
第4讲 李群与李代数 - Sophus库安装
Sophus安装过程: $ git clone https://github.com/strasdat/Sophus.git $ cd Sophus $ git checkout a621ff $ mkdir build // 创建外部构建编译输出目录 $ cd build $ cmake -DCMAKE_INSTALL_PREFIX=/usr/local .. // 外部构建,
《视觉 SLAM 十四讲》V2 第 4 讲 李群与李代数 【什么样的相机位姿 最符合 当前观测数据】
P71 文章目录 4.1 李群与李代数基础4.1.3 李代数的定义4.1.4 李代数 so(3)4.1.5 李代数 se(3) 4.2 指数与对数映射4.2.1 SO(3)上的指数映射罗德里格斯公式推导 4.2.2 SE(3) 上的指数映射SO(3),SE(3),so(3),se(3)的对应关系 4.3 李代数求导与扰动模型4.3.2 SO(3)上的李代数求导4.3.3 李代数求导4.
【SLAM数学基础】李群与李代数 BCH近似公式
三维旋转构成了三维旋转群 SO(3),其对应的李代数为 s o \mathfrak{so} so(3);三维变换构成了三维变换群 SE(3),其对应的李代数为 s e \mathfrak{se} se(3)。 1.指数映射 李代数元素到李群元素的映射为指数映射,其中 s o \mathfrak{so} so(3) 至 SO(3) 的指数映射为: exp ( ϕ ∧ ) = R =