无理数专题
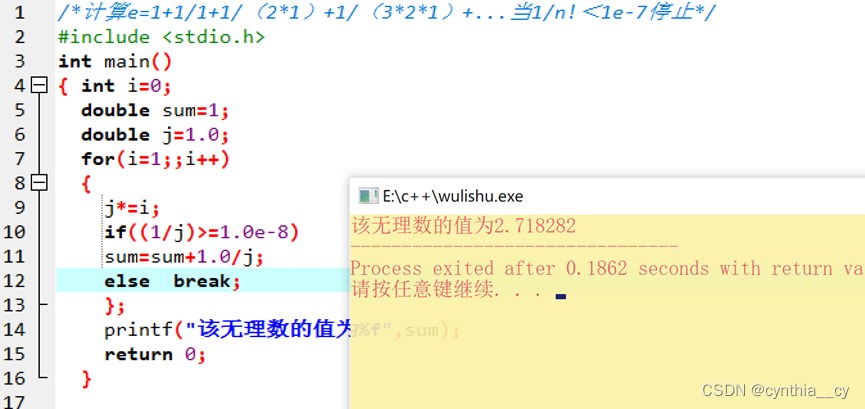
例6计算无理数e的值
计算e=1+1/1+1/(2*1)+1/(3*2*1)+...当1/n!<1e-7停止 for循环结构中嵌套 if else二分支结构 进行sum的累加判断,最后break 跳出循环,输出sum #include <stdio.h>int main(){ int i=0;double sum=1;double j=1.0;for(i=1;;i++){j*=i; if((1/j)>=1.0e
欧几里得证明$\sqrt{2}$是无理数
选自《费马大定理:一个困惑了世间智者358年的谜》,有少许改动。 原译者:薛密 \(\sqrt{2}\)是无理数,即不能写成一个分数。欧几里得以反证法证明此结论。第一步是假定相反的事实是真的,即\(\sqrt{2}\)可以写成某个未知的分数。用\(\frac{p}{q}\) 来代表这个假设的分数,其中 \(p\) 和 \(q\) 是两个整数。 在开始证明本身之前,需要对分数和偶数的某些性质有个
如何证明根号2,3是无理数
1.问题 推广成,如何证明 根号 p(p是素数)是无理数 素数:一个大于1的自然数,如果除了1和它自身外,不能被其他自然数整除(除0以外)的数称之为素数。 2.思路 反证法: 假如 ( p ) = a b \sqrt{(p)} = \frac{a}{b} (p) =ba 其中, a, b互质的整数。 然后, a 2 = p b 2 a^2 = p b^2 a2=pb2 假如 a
超级计算机算圆周率有多快,既然π是无理数,为什么超级计算机还要一直计算呢?真能算尽吗?...
既然π是无理数,为什么超级计算机还要一直计算呢?真能算尽吗? 圆周率是个很神奇的数字,世界上不知道有多少的数学家一生都痴迷于它。当它第一次被发现的时候,就因为它拥有无限不循环的特性而惊奇整个世界。之后随着大家对于数字的研究深入,开始慢慢的想要去算清圆周率的准确长度。不过圆周率却一直被无限不循环这个框架局限着,这些年来,也有很多数学家想要将这一局限打破,但是却都没有成功。虽然经历了一次一次的失败,
高等数学Mathematica实验题——无理数π和e的小数点以后1000位的近似值的求解与输出
第一个实验题:用Mathematica软件写出两个重要的无理数π和e的小数点以后1000位的近似值 解答: 备注:还好在Excel中进行了验证,如果输入N[π,1000],只能得到小数点以后999位的近似值。再次说明测试的重要性!
学习记忆——数学篇——算术——无理数
谐音记忆法 2 \sqrt{2} 2 ≈1.41421:意思意思而已;意思意思; 3 \sqrt{3} 3 ≈1.7320:—起生鹅蛋;一起生儿; 5 \sqrt{5} 5 ≈2.2360679:两鹅生六蛋(送)六妻舅;儿儿生(出来就是)遛 7 \sqrt{7} 7 ≈2.6457513:二妞是我,气我一生;二流是我 8 \sqrt{8} 8 =2√2
学习记忆——数学篇——算术——无理数
谐音记忆法 2 \sqrt{2} 2 ≈1.41421:意思意思而已;意思意思; 3 \sqrt{3} 3 ≈1.7320:—起生鹅蛋;一起生儿; 5 \sqrt{5} 5 ≈2.2360679:两鹅生六蛋(送)六妻舅;儿儿生(出来就是)遛 7 \sqrt{7} 7 ≈2.6457513:二妞是我,气我一生;二流是我 8 \sqrt{8} 8 =2√2