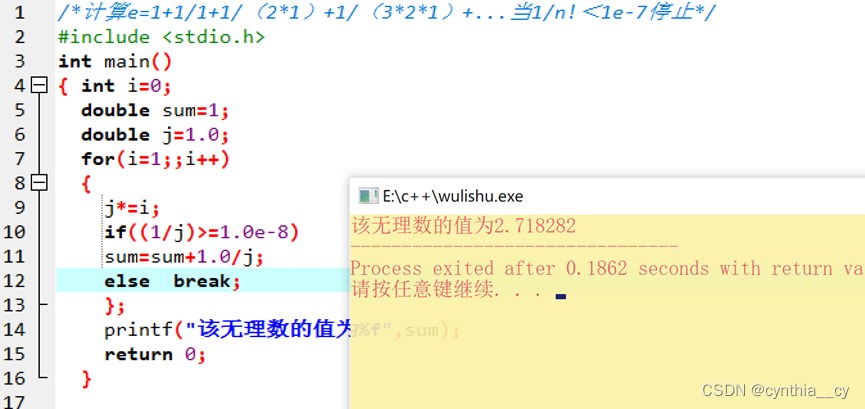
本文主要是介绍无理数的渊源,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
无理数-西方欧美数学史上的第1次危机
第一次数学危机是数学史上的一次重要事件,发生于公元前400年左右的古希腊时期。这次危机的出现冲击了一直以来在西方数学界占据主导地位的毕达哥拉斯学派,同时标志着西方世界关于无理数的研究的开始。
古希腊的毕达哥拉斯学派认为“万物皆数”,数就是正整数,正整数也就是组成物质的基本粒子——原子。该学派的一个青年希帕斯,首先发现了正方形边与对角线之比不能用整数之比表示,即根号2不是分数。由于希帕斯的发现和这个学派的错误信条相抵触,因而他被这个学派的其他成员抛入海中淹死了。
这一发现使毕达哥拉斯学派的人感到迷惑不解,它不仅违背了毕达哥拉斯派的信条,而且冲击着当时希腊人持有的“一切量都可以用有理数表示”的信仰。通常人们就把希帕索斯发现的这个矛盾,叫做希帕索斯悖论。这次数学危机导致数学研究对象从有理数推广到无理数,进一步促使人们从依靠直观感觉与经验转向依靠证明,推动了公理几何学与逻辑学的诞生和发展。
毕达哥拉斯:即发现了勾股定理的那位家喻户晓的数学家,勾股定理(◺直角三角形中,两直边的平方和等于斜边的平方)。
无理数-东方数学史上的发现
在东方数学史上,无理数的发现可以追溯到古代中国。然而,由于历史记载的限制和文化背景的差异,很难确定一个具体的事件或人物作为东方数学史上第一次发现无理数的标志。
在古代中国,数学家们对数学的研究主要集中在算术、代数和几何等领域。虽然没有像西方数学史上那样明确的“第一次数学危机”,但中国古代数学家们也对无理数有了一定的认识和研究。
例如,在《九章算术》中,就有关于开方不尽的数的讨论。这些数不能表示为两个整数的比值,类似于无理数的概念。此外,中国古代数学家还研究了圆周率等数学常数,这些常数也具有无理数的性质。
总的来说,东方数学史上对无理数的认识和研究是一个逐渐发展的过程,与西方数学史有所不同。虽然没有一个明确的第一次发现无理数的事件,但古代东方数学家们的工作为后来对无理数的深入研究奠定了基础。
这篇关于无理数的渊源的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!