康托专题
24.9.1(康托展开)
上星期三: 补 24牛客多校 二 C 牛客传送门 思路: 赛时写模拟写的很臭,如果用dp写就很方便 代码如下: const int N=2e6+10;const int mod=1e9+7;ll n;char s[N][2];int dp[N][2];void solve(){c
HDU 1043 搜索+康托展开
反向搜索 然后把所有的状态都打表出来 用康托展开记录hash判重 #include "string"#include "iostream"#include "algorithm"#include "queue"using namespace std;const int maxn=1000001;struct node{int s[9];int loc; //0的位置int st
【UVAlive】康托展开的思想
题目链接:点击打开链接 题目大意:就是给你一个n 求0~n之间的数 的k-进制和(-k)进制相同的数目 题目分析:要是的k和(-k)进制的数相同,那么就是在转化为k(-k)进制之后,在奇数位上 为全零。 对于n在转化为长度为len的k进制数后 从最高位开始“递归”看 即康托展开的思想。 #inclu
Mathematica 一个基于康托集合定义的函数
原文:无限小却无限大的集合 & 阶梯状的连续函数 部分内容摘要: 康托集合是闭区间[0,1]的子集,它的定义如下:给定区间[0,1],把这个区间分成三段,去掉中间那一端(即去掉(1/3,2/3)),然后把剩下的两段中每一段都按照刚才的方法再进行操作,然后再分,再分,就这样一直挖洞挖下去。在第二次操作后,剩下的区间是[0,1/9]∪[2/9,1/3]∪[2/3,7/9]∪[8/9,1],再操作一
hdu1430魔板(BFS+康托展开)
做这题先看:http://blog.csdn.net/u010372095/article/details/9904497 Problem Description 在魔方风靡全球之后不久,Rubik先生发明了它的简化版——魔板。魔板由8个同样大小的方块组成,每个方块颜色均不相同,可用数字1-8分别表示。任一时刻魔板的状态可用方块的颜色序列表示:从魔板的左上角开始,按顺时针方向依次写
历届试题 九宫重排 (bfs+康托展开(哈希))
问题描述 如下面第一个图的九宫格中,放着 1~8 的数字卡片,还有一个格子空着。与空格子相邻的格子中的卡片可以移动到空格中。经过若干次移动,可以形成第二个图所示的局面。 我们把第一个图的局面记为:12345678. 把第二个图的局面记为:123.46758 显然是按从上到下,从左到右的顺序记录数字,空格记为句点。 本题目的任务是已知九宫的初态和终态,求最少经过多少步的
Eight HDU - 1043(八数码, 康托展开+逆向BFS打表)
Eight 题目链接: HDU - 1043题意: <1> 图 <2> 图 要求由<1>图变到<2>图, 求出路径; 每块格子只能和上下左右四个方向的格子交换, 网上有用A*写的, 不需要那么麻烦, 逆向BFS加上康托展开剪枝就可以;(C++过的, G++超内存
康托展开,求某个排列在字典序排的位置
遇到一个编程题,考核的内容就是康托展开问题,这里就重新描述下 X=a[n]*(n-1)!+a[n-1]*(n-2)!+...+a[i]*(i-1)!+...+a[1]*0! 其中,a[i]为整数,并且X=a[n]*(n-1)!+a[n-1]*(n-2)!+...+a[i]*(i-1)!+...+a[1]*0!。这就是康托展开。康托展开可用代码实现。推导过程大家有兴趣可以自己去找资料,这里我就直接
康托展开(Cantor Expansion)
【康托展开简介】康托展开(Cantor Expansion)是一种特殊的哈希函数,是一个相对快速的判重方法,其时间复杂度为O(n^2),其中 n 是集合中元素的个数。康托展开能够判重,依据的是一个集合各元素产生的全部排列中各个排列的位序 id。而位序 id 的计算公式如下: 其中,a[i] 的值为某个排列中第 i 位右边各位中字典序小于第 i 位的字符的个数,且0≤a[i]<i,1≤i≤n。 利用
康托超穷基数序列的原型研究进度
计算机程序将用在数学计算上。高性能计算实质是高等数学计算,高等代数和概论的计算。 无限分割和无穷大是产生极限的两个无限性,但是在实际应用中,任何时刻都不存在无限分割和无穷大。因此,在积极无限的基础上,无穷大与时间的无限相联系,表示无限的延续,受到物质有限的限制,是一个与未来相关的未知量;对已知量的无限分割受到时间和物质最小单位的限制,实际上是不存在的,无限分割一定是基于模糊(不确定的
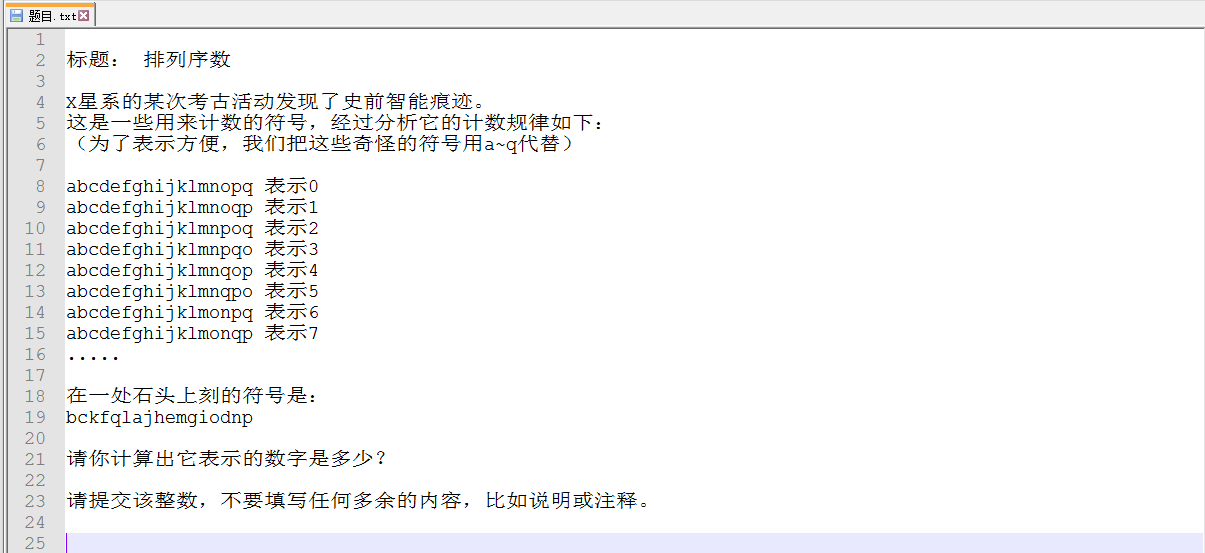
2017蓝桥杯官方模拟题 排列序数(康托展开)
题目: 思路: 康托展开模板题 代码: #include <stdio.h>#include <string.h>#include <string>#include <iostream>#include <stack>#include <queue>#include <vector>#include <algorithm>#define mem(a,b) mems
NYOJ139 我排第几个(数论,康托展开模板题)
题目: 我排第几个 时间限制: 1000 ms | 内存限制: 65535 KB 难度: 3 描述 现在有"abcdefghijkl”12个字符,将其所有的排列中按字典序排列,给出任意一种排列,说出这个排列在所有的排列中是第几小的? 输入 第一行有一个整数n(0<n<=10000); 随后有n行,每行是一个排列; 输出 输出一个整数m,占一行,m表示排列是第几位