本文主要是介绍Mathematica 一个基于康托集合定义的函数,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
原文:无限小却无限大的集合 & 阶梯状的连续函数
部分内容摘要:
康托集合是闭区间[0,1]的子集,它的定义如下:给定区间[0,1],把这个区间分成三段,去掉中间那一端(即去掉(1/3,2/3)),然后把剩下的两段中每一段都按照刚才的方法再进行操作,然后再分,再分,就这样一直挖洞挖下去。在第二次操作后,剩下的区间是[0,1/9]∪[2/9,1/3]∪[2/3,7/9]∪[8/9,1],再操作一次后区间将由8段构成。
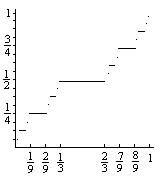
设f为定义域在康托集合内的函数,定义f(x)为按照上面的转化方法x所对应的二进制小数,显然这个函数的值域就是[0,1]。比如1/3的三进制为0.0222…,而二进制0.01111…=0.1即十进制的1/2,因此f(1/3)=1/2。我们发现,2/3的三进制为0.2,而0.1的十进制也是1/2。于是f(1/3)=f(2/3)。类似地,那些被挖去的区间的两个端点对应的函数值都相同。现在,我们把这个函数的定义域也扩展到[0,1]:让康托集合里的那些被挖去的区间里的点的函数值与该区间对应的端点相同(在函数图象上看相当于把函数值相等的点用横线段连起来)。于是,f(1/2)=f(1/3)=f(2/3)=1/2,f(1/8)=f(1/9)=f(2/9)=1/4。这个函数一定是上升函数,它在长度为1的区间里从0增长到了1。同时,这个函数也是一个连续函数,因为康托集合与[0,1]的所有实数一一对应。这个函数是一个阶梯状的函数,但是它不是分段的,是连续的。它是无穷多个横线段组成的一个连续函数,除端点无意义以外导数值都是0。或者说,这个函数在不变之中上升。
Mathematica实现如下:
cantor[x_,n_,z_,low_,upp_]:=If[x<2/3low+1/3upp,
cantor[x,n+1,z-1/2^n,low,2/3low+1/3upp],
If[x>1/3low+2/3upp,
cantor[x,n+1,z+1/2^n,1/3low+2/3upp,upp],
z]]
cantor[x_]:=cantor[x,2,.5,0,1]
效果截图

这篇关于Mathematica 一个基于康托集合定义的函数的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





