平方根专题
Leetcode JAVA刷刷站(69)x的平方根
一、题目概述 二、思路方向 在Java中,计算一个非负整数x的算术平方根,并返回其整数部分,你可以使用二分查找法。这是因为平方根函数是单调递增的,所以我们可以利用二分查找在合理的时间复杂度内找到结果。 三、代码实现 public class Solution { public int mySqrt(int x) { if (x == 0) { retur
leetcode 二分查找·系统掌握 x的平方根
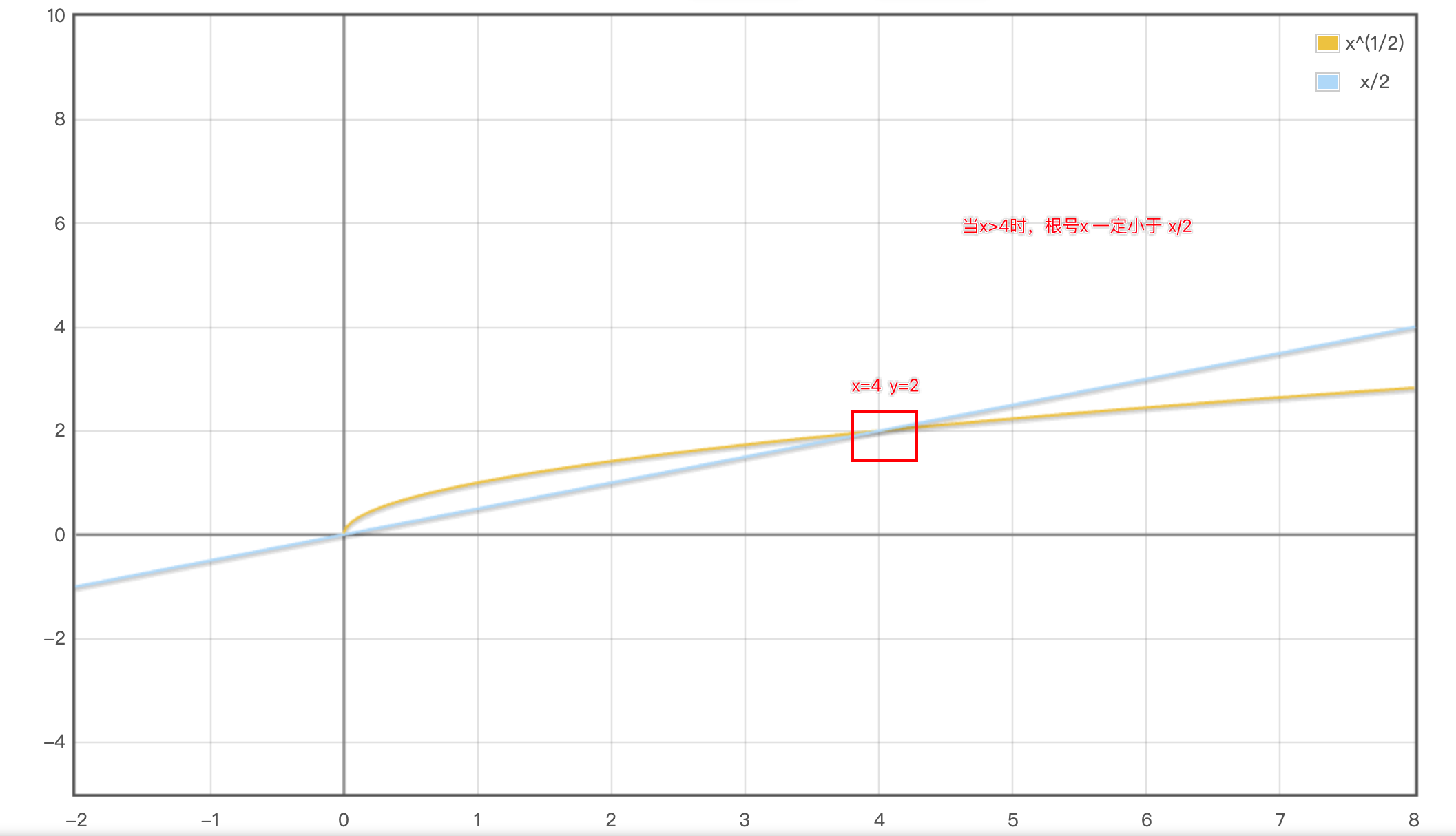
题目: 题解 这题可以使用~01~泛型查找在0~x/2的范围内查找答案。 int mySqrt(int x) {long l=0,r=x,mid;while(l<r){mid=(l+r+1)>>1;if(mid*mid>x)r=mid-1;else l=mid;}//因为一定有答案所以不用判定是否查找失败return l;}
迭代快速算平方根的c++程序(Carmack的QUAKE3)
链接:http://www.zhihu.com/question/20396457/answer/23658441 来源:知乎 /* ================ SquareRootFloat ================ */#include <iostream> float SquareRootFloat(float number) {
基础数学-求平方根(easy)
一、问题描述 二、实现思路 1.题目不能直接调用Math.sqrt(x) 2.这个题目可以使用二分法来缩小返回值范围 所以我们在left<right时 使 mid = (left+right)/2+1 当mid*mid>x时,说明right范围过大,right=right-1 当mid*mid<x时,说明left范围太小,l
不用函数库求一个数的平方根 (java版)
一、题目 编写程序求一个整数的平方根,精确到小数点后三位 二、解法 1) 采用 牛顿迭代法。 2)牛顿迭代法简介 假设方程 在 附近有一个根,那么用以下迭代式子: 依次计算、、、……,那么序列将无限
二分查找应用-计算开平方根
问题: 计算开平方根 解题思路 1.二分查找,时间复杂度O(nlog(n)),空间复杂度O(1) 2.牛顿法,时间复杂度O(nlog(n)),空间复杂度O(1),收敛速度较快. 代码如下 public static void main(String[] args) {int x = 8;int ans = mySqrt2(x);System.out.println(ans);int an
算法第三天力扣第69题:X的平方根
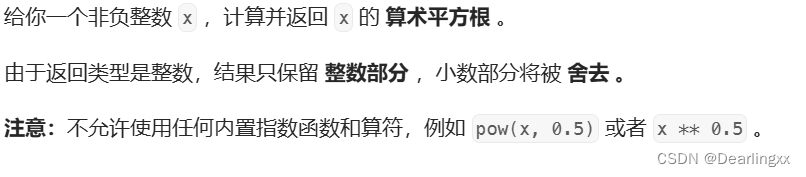
69. x 的平方根 (可点击下面链接或复制网址进行做题) https://leetcode.cn/problems/sqrtx/https://leetcode.cn/problems/sqrtx/ 给你一个非负整数 x ,计算并返回 x 的 算术平方根 。 由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。 注意:不允许使用任何内置指数函数和算符,例如
leetcode(js) 69. x 的平方根
x 的平方根 实现 int sqrt(int x) 函数。 计算并返回 x 的平方根,其中 x 是非负整数。 由于返回类型是整数,结果只保留整数的部分,小数部分将被舍去。 示例 1: 输入: 4 输出: 2 示例 2: 输入: 8 输出: 2 说明: 8 的平方根是 2.82842…, 由于返回类型是整数,小数部分将被舍去。 解题思路:直接使用Math.sqrt()求平方根,舍去小数部
C语言试题五十四之求n以内(不包括n)同时能被3与7整除的所有自然数之和的平方根s,并作为函数值返回。
📃个人主页:个人主页 🔥系列专栏:C语言试题200例目录 💬推荐一款刷算法、笔试、面经、拿大公司offer神器 👉 点击跳转进入网站 ✅作者简介:大家好,我是码莎拉蒂,CSDN博客专家(全站排名Top 50),阿里云博客专家、51CTO博客专家、华为云享专家 1、题目 请编写一个函数double function(int n),其功能时:求n以内(不包括n)同时能被3与7整除的所
【C++】二分查找算法:x的平方根
1.题目 2.算法思路 看到题目可能不容易想到二分查找。 这题考察我们对算法的熟练程度。 二分查找的特点:数组具有二段性(不一定有序)。 题目中没有数组,我们可以造一个从0到x的数组,然后利用二分查找找到对应的值即可。 3.代码 class Solution {public:int mySqrt(int x) {long long left=0,right=x;while(
Leetcode——x的平方根
实现 int sqrt(int x) 函数。 计算并返回 x 的平方根,其中 x 是非负整数。 由于返回类型是整数,结果只保留整数的部分,小数部分将被舍去。 示例 1: 输入: 4 输出: 2 示例 2: 输入: 8 输出: 2 说明: 8 的平方根是 2.82842…, 由于返回类型是整数,小数部分将被舍去。 思路: 典型的二分法问题,while循环比较目标值与中间值平方的关系,所以
二分搜索小结-x的平方根
二分查找法作为一种常见的查找方法,将原本是线性时间提升到了对数时间范围,大大缩短了搜索时间,具有很大的应用场景,而在LeetCode中,要运用二分搜索法来解的题目也有很多,但是实际上二分查找法的查找目标有很多种,而且在细节写法也有一些变化。 第一类: 需查找和目标值完全相等的数 这是最简单的一类,也是我们最开始学二分查找法需要解决的问题,比如我们有数组[2, 4, 5, 6, 9],targe
二分查找向下取整导致的死循环69. x 的平方根
二分查找向下取整导致的死循环 考虑伪题目:从数组arr中查找出目标元素target对应的下标,如果数组中不存在目标元素,找 到第一个元素值小于target的元素的下标。 编写二分查找算法如下: @Testvoid testBinarySearch(){int[] arr = new int[]{1, 2};int left = 0, right =
[PTA] 习题2-5 求平方根序列前N项和
本题要求编写程序,计算平方根序列1+2+3+⋯的前N项之和。可包含头文件math.h,并调用sqrt函数求平方根。 输入格式: 输入在一行中给出一个正整数N。 输出格式: 在一行中按照“sum = S”的格式输出部分和的值S,精确到小数点后两位。题目保证计算结果不超过双精度范围。 输入样例: 10结尾无空行 输出样例: sum = 22.47结尾无空行 代码: #
力扣69 x的平方根 二分查找求平方根 C语言
题目 给你一个非负整数 x ,计算并返回 x 的 算术平方根 。 由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。 注意:不允许使用任何内置指数函数和算符,例如 pow(x, 0.5) 或者 x ** 0.5 。 示例 1: 输入:x = 4输出:2 示例 2: 输入:x = 8输出:2解释:8 的算术平方根是 2.82842..., 由于返回类型是整数
C语言 | Leetcode C语言题解之第69题x的平方根
题目: 题解: int mySqrt(int x) {long int i = 0;for(i=0;;i++){long int a = i*i;long int b = (i+1)*(i+1);if(a <= x&&b > x){break;}}return i;}
完全平方数的判定及整数平方根的快速求解
在上个星期的“有道难题”网络预赛中,某些Group的第二题涉及到了完全平方数的判定问题。相信大多数人的判定语句都差不多是这样写的:if(sqr((int)sqrtl(n))==n){...},把这条语句整理一下,大概是这样: inline __int64 sqr( int n){ return static_cast<__int64>(n)*n;} inline int dir
LeetCode 69—— x 的平方根
阅读目录 1. 题目2. 解题思路一3. 代码实现一4. 解题思路二5. 代码实现二 1. 题目 2. 解题思路一 二分查找法,对于整数 i ∈ [ 0 , x ] i \in [0,x] i∈[0,x],我们判断 i 2 i^2 i2 和 x x x 的关系,然后找到最后一个平方小于等于 x x x 的整数即可。 需要注意,为了避免求平方的时候整数溢出,需要选
【 LeetCode 】69、x的平方根
题目描述 实现 int sqrt(int x) 函数。计算并返回 x 的平方根,其中 x 是非负整数由于返回类型是整数,结果只保留整数的部分,小数部分将被舍去 Math.sqrt(x) 使用较为取巧的办法 直接使用Math.sqrt() var mySqrt = function (x) {// 直接调用Math.sqrt()函数return Math.floor(Math.sqrt(x)
leetcode题目69:x的平方根【python】
题目描述 计算并返回 x 的平方根,其中 x 是非负整数。 由于返回类型是整数,结果只保留整数部分,小数部分将被舍去。 输入格式 x:一个非负整数。 输出格式 返回整数部分的平方根。 示例 示例 1 输入: x = 4输出: 2 示例 2 输入: x = 8输出: 2解释: 8 的平方根是 2.82842..., 因为返回类型是整数,小数部分将被舍去。 方法一
x的平方根(二分查找实现)
设计函数int sqrt(int x),计算 xx 的平方根。 import java.util.Scanner;public class MySqrt public static int sqrt(int n){int left=1,right=(n+1)/2;while(left<right){int mid=(left+right)/2;int result= mid*mid;// int
模块三:二分——69.x的平方根
文章目录 题目描述算法原理解法一:暴力查找解法二:二分查找 代码实现暴力查找C++Java 题目描述 题目链接:69.x的平方根 算法原理 解法一:暴力查找 依次枚举 [0, x] 之间的所有数 i (这⾥没有必要研究是否枚举到 x / 2 还是 x / 2 + 1 。因为我们找到结果之后直接就返回了,往后的情况就不会再判断。反⽽研究枚举区间,既耽误时间,⼜可能出错)
python练习 二数求和,求平方根,计算圆的面积,随机数,摄氏度转华氏摄氏度,判断是否是数字
二数求和 # 二数求和def sum_count():a1 = float(input("请输入第一个数"))a2 = float(input("请输入第二个数"))print("二数之和为{}".format(a1 + a2)) 求平方根 # 求平方根 相当于 cmath 中的sqrtdef squar_num():a = float(input("请输入一个整数"))print("
Leetcode-69.x的平方根
题目描述 给你一个非负整数 x ,计算并返回 x 的 算术平方根 。 由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。 注意:不允许使用任何内置指数函数和算符,例如 pow(x, 0.5) 或者 x ** 0.5 。 示例 1: 输入:x = 4 输出:2 示例 2: 输入:x = 8 输出:2 解释:8 的算术平方根是 2.82842…, 由于返回类型是整数,小数部分
求1000以内正整数的平方根(C语言)
一、运行结果; 二、源代码; # define _CRT_SECURE_NO_WARNINGS# include <stdio.h># include <math.h>int main(){//初始化变量值;int number = 0;int result = 0;//提示用户;printf("请输入1000以内求平方根的数据:");//获取用户输入的值;scanf("%d", &