密度估计专题
区间预测 | Matlab实现BP-ABKDE的BP神经网络自适应带宽核密度估计多变量回归区间预测
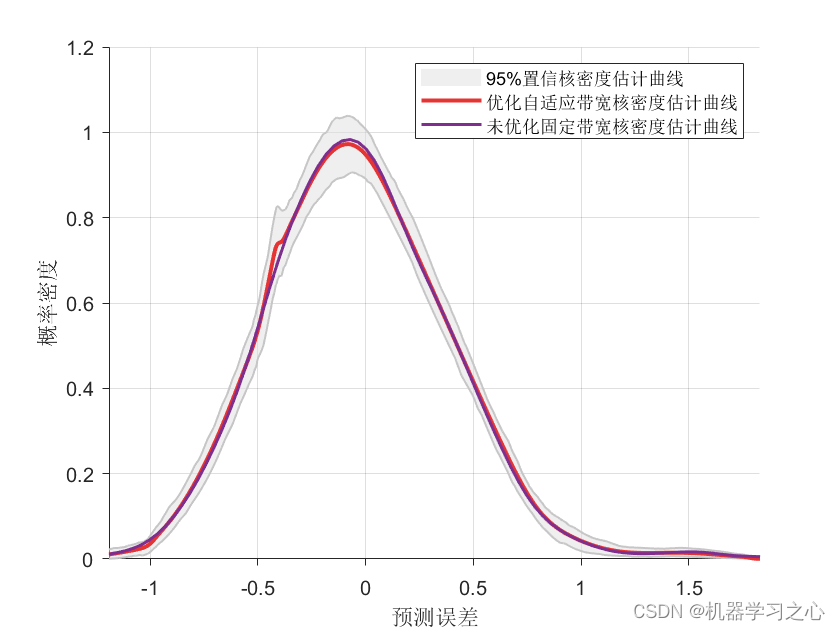
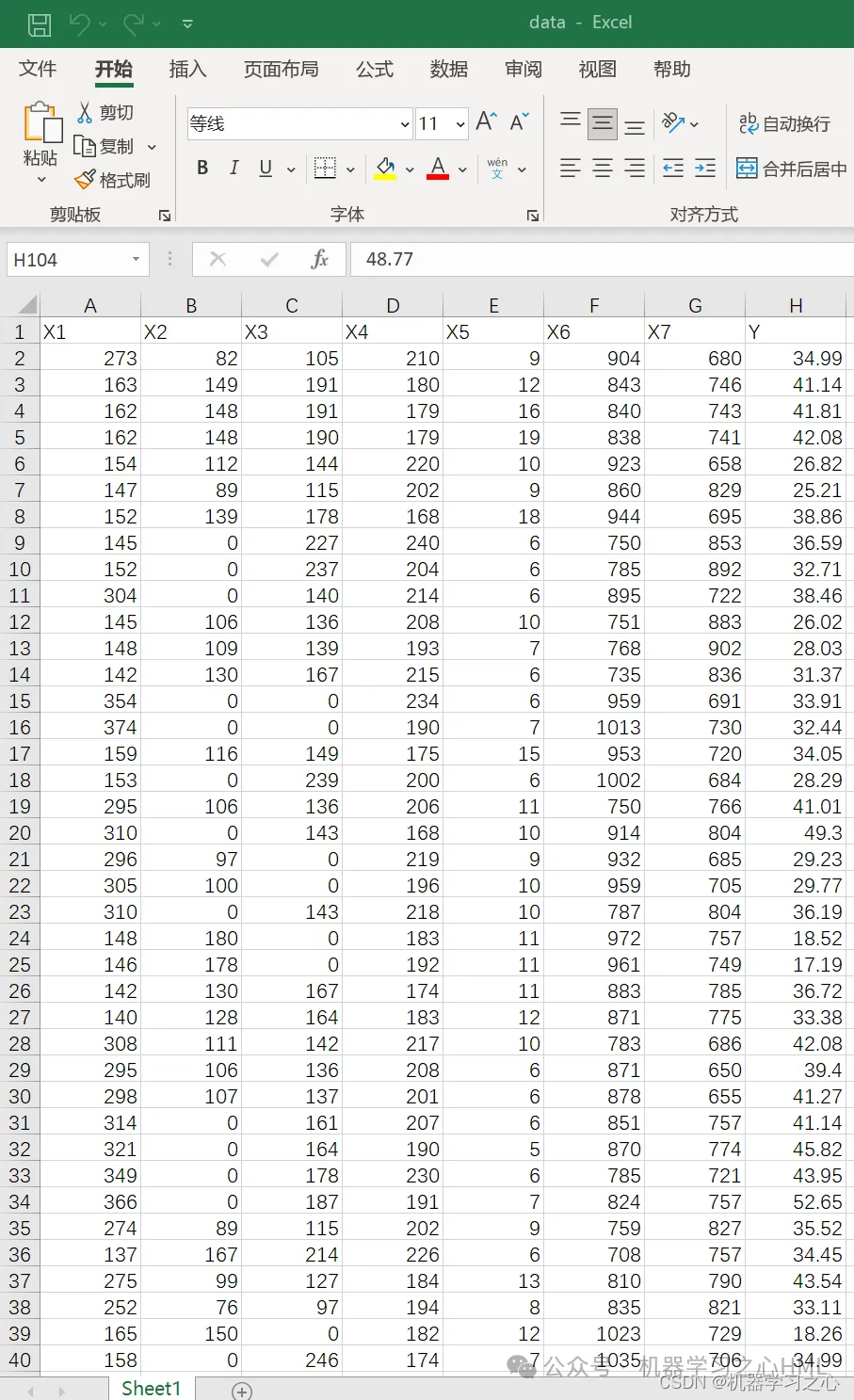
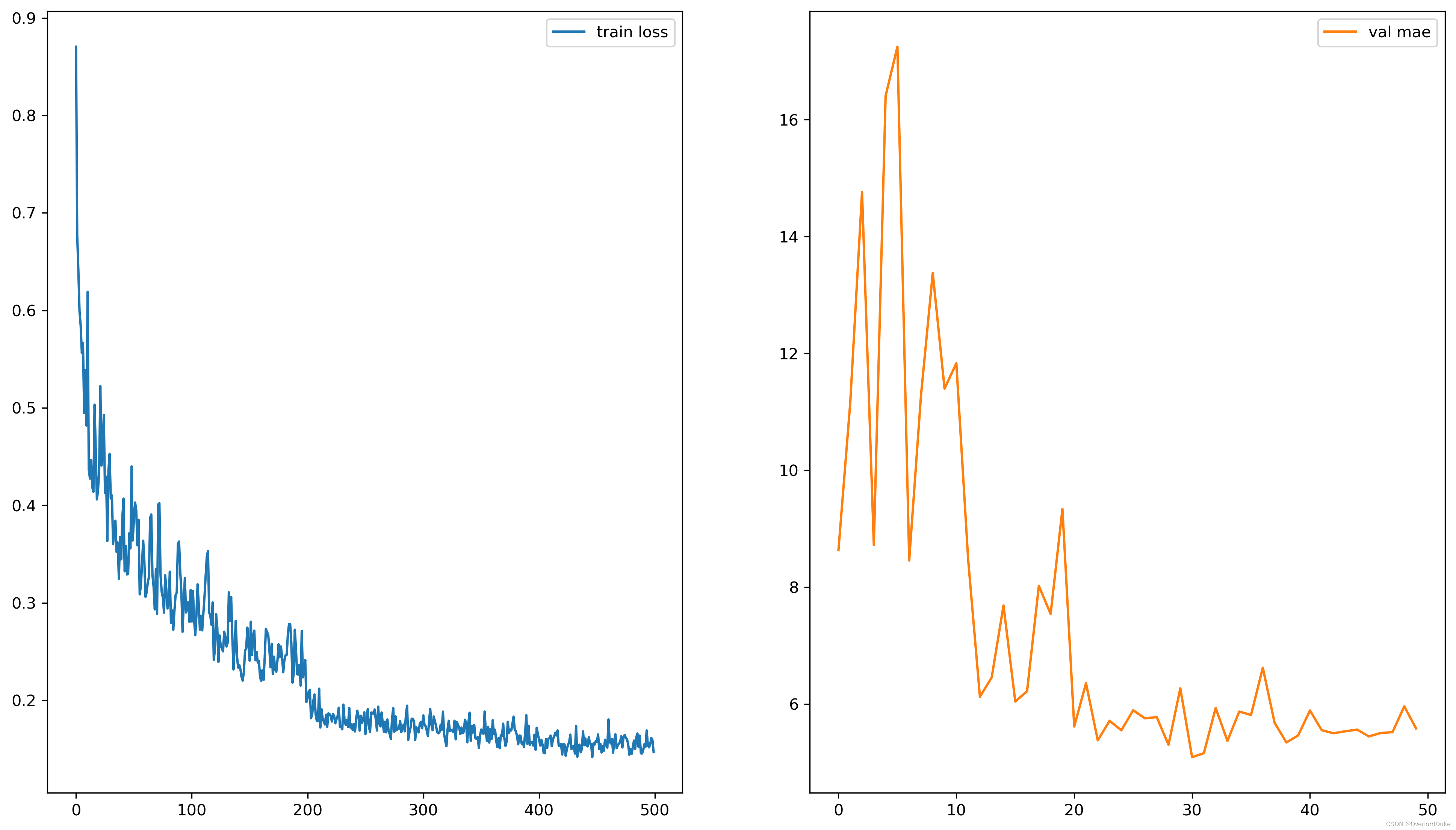
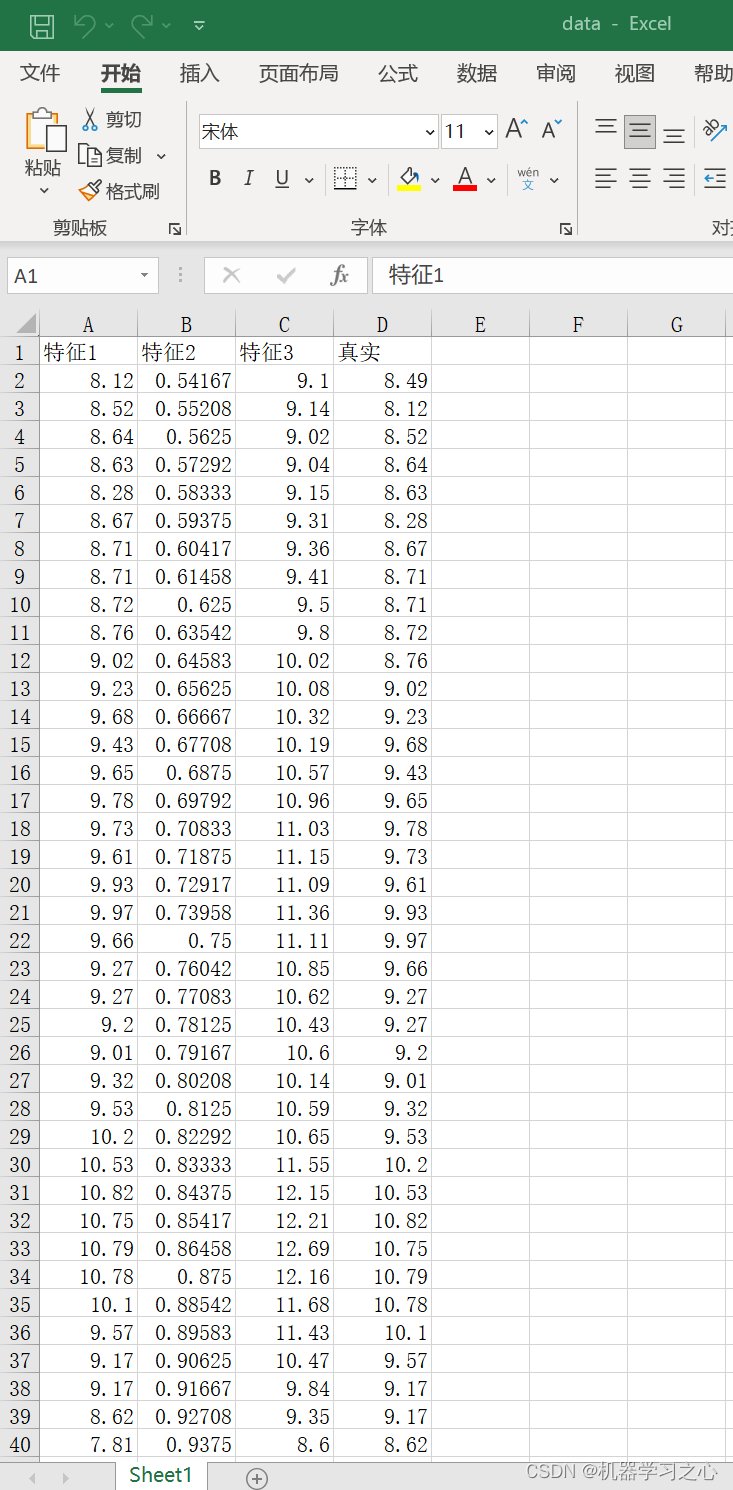
区间预测 | Matlab实现BP-ABKDE的BP神经网络自适应带宽核密度估计多变量回归区间预测 目录 区间预测 | Matlab实现BP-ABKDE的BP神经网络自适应带宽核密度估计多变量回归区间预测效果一览基本介绍程序设计参考资料 效果一览 基本介绍 1.Matlab实现BP-ABKDE的BP神经网络自适应带宽核密度估计多变量回归区间预测(完整源码和数据)
区间预测 | Matlab实现EVO-CNN-SVM能量谷算法优化卷积神经网络支持向量机结合核密度估计多置信区间多变量回归区间预测
区间预测 | Matlab实现EVO-CNN-SVM能量谷算法优化卷积神经网络支持向量机结合核密度估计多置信区间多变量回归区间预测 目录 区间预测 | Matlab实现EVO-CNN-SVM能量谷算法优化卷积神经网络支持向量机结合核密度估计多置信区间多变量回归区间预测效果一览基本介绍程序设计参考资料 效果一览 基本介绍 1.Matlab实现EVO-CNN-SVM
区间预测 | Matlab实现LSTM-ABKDE长短期记忆神经网络自适应带宽核密度估计多变量回归区间预测
区间预测 | Matlab实现LSTM-ABKDE长短期记忆神经网络自适应带宽核密度估计多变量回归区间预测 目录 区间预测 | Matlab实现LSTM-ABKDE长短期记忆神经网络自适应带宽核密度估计多变量回归区间预测效果一览基本介绍程序设计参考资料 效果一览 基本介绍 1.Matlab实现LSTM-ABKDE长短期记忆神经网络结合自适应带宽核函数密度估
使用python绘制核密度估计图
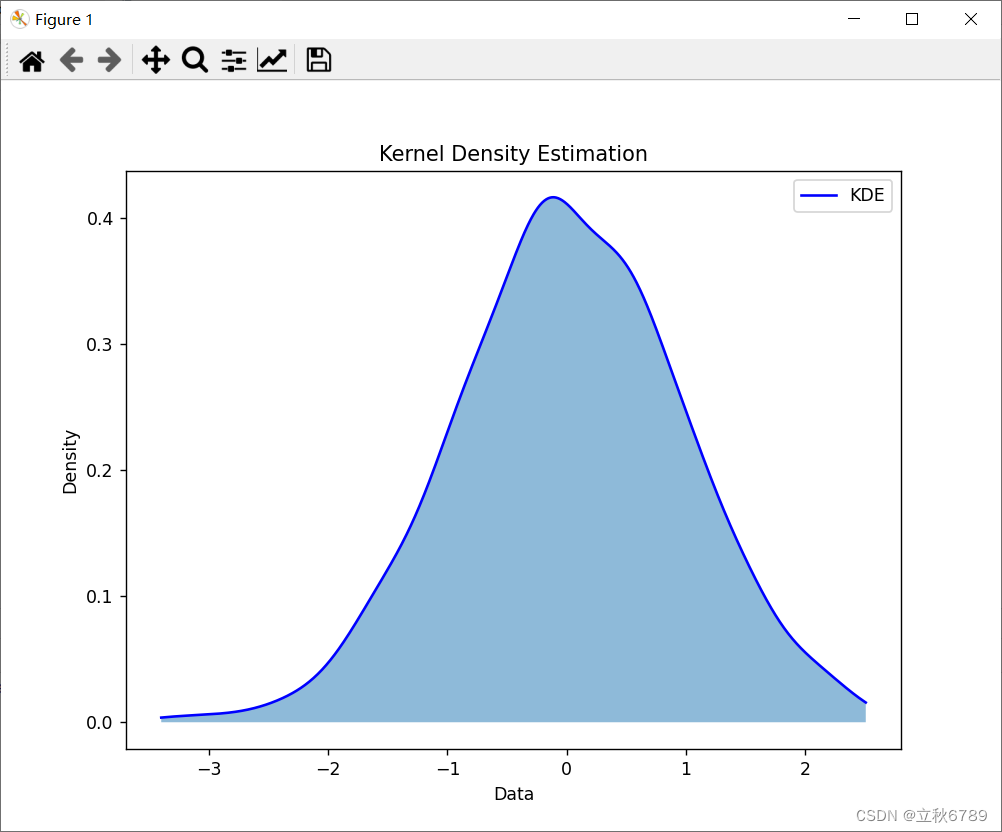
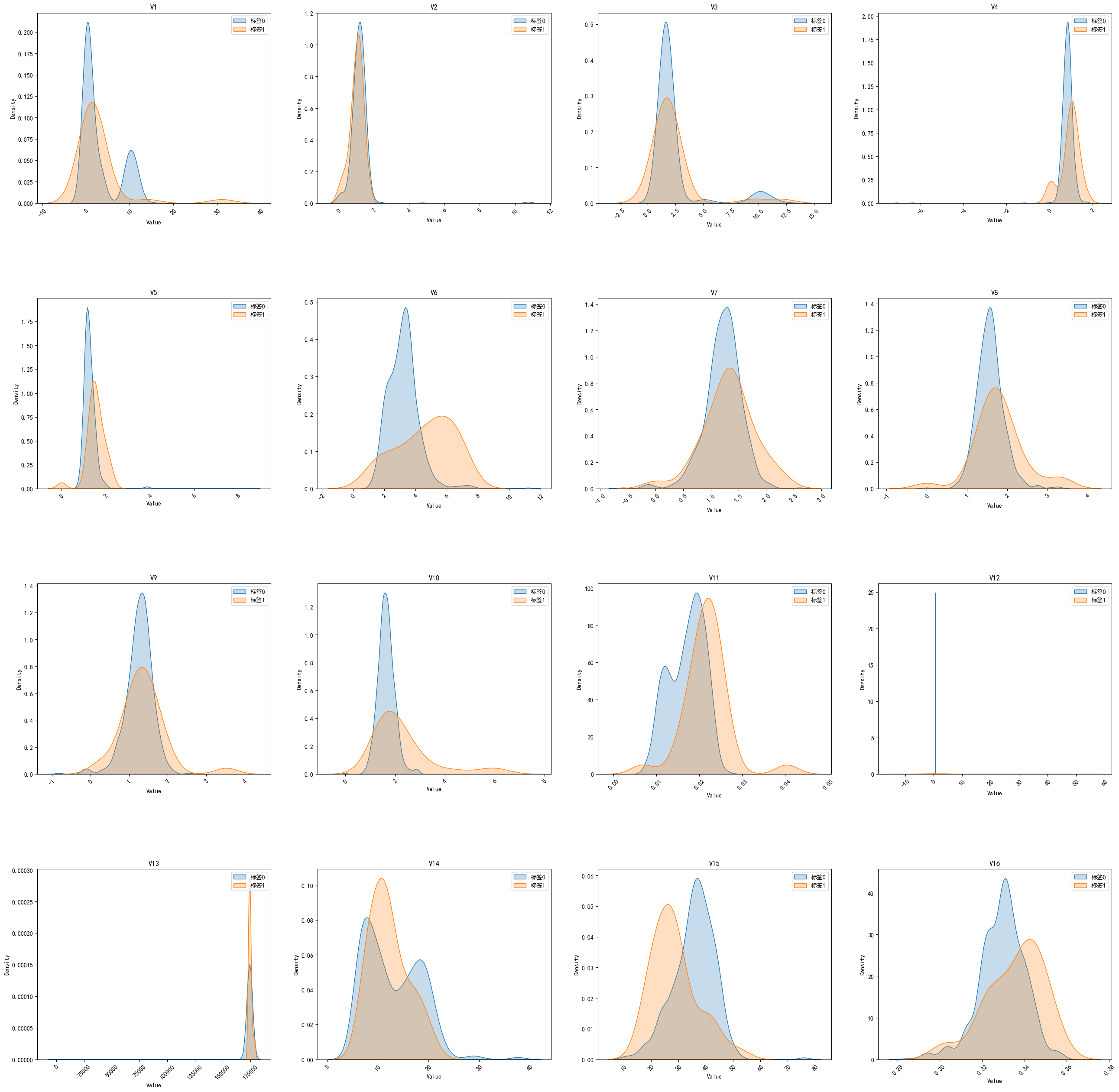
使用python绘制核密度估计图 核密度估计图介绍效果代码 核密度估计图介绍 核密度估计(Kernel Density Estimation,KDE)是一种用于估计数据概率密度函数的非参数方法。与直方图不同,KDE 可以生成平滑的密度曲线,更好地反映数据的分布情况。核密度估计图(KDE 图)通过将核函数(通常是高斯核)应用于每个数据点,并将这些核函数的和作为密度估计来生成。 效
LSTM-KDE的长短期记忆神经网络结合核密度估计多变量回归区间预测(Matlab)
LSTM-KDE的长短期记忆神经网络结合核密度估计多变量回归区间预测(Matlab) 目录 LSTM-KDE的长短期记忆神经网络结合核密度估计多变量回归区间预测(Matlab)效果一览基本介绍程序设计参考资料 效果一览 基本介绍 1.LSTM-KDE的长短期记忆神经网络结合核密度估计多变量回归区间预测(Matlab)。 2.含点预测图、置信区间预测图
区间预测 | PSO-RF-KDE的粒子群优化随机森林结合核密度估计多变量回归区间预测(Matlab)
区间预测 | PSO-RF-KDE的粒子群优化随机森林结合核密度估计多变量回归区间预测(Matlab) 目录 区间预测 | PSO-RF-KDE的粒子群优化随机森林结合核密度估计多变量回归区间预测(Matlab)效果一览基本介绍程序设计参考资料 效果一览 基本介绍 1.Matlab实现PSO-RF-KDE的粒子群优化随机森林结合核密度估计多变量回归区间预
“傻瓜”学计量——核密度估计KDE
提纲: 什么是核密度估计,是干什么的 代码 1 前言 参数估计vs非参数估计参数估计是样本数据来自一个具有明确概率密度函数的总体。非参数估计是样本数据的概率分布未知,这时,为了对样本数据进行建模,需要估计样本数据的概率密度函数。 核密度估计Kernel Density Estimation即是非参数估计的一种方式。即,核密度估计的目的:就是估测所给样本数据的概率密度函数。在论
基于r语言的疾病制图中自适应核密度估计的阈值选择方法案例
背景 诸如核密度估计(KDE)的平滑方法被用于控制用于计算每种疾病率的空间支持的群体基础。平滑程度由用户定义的参数(带宽或阈值)控制,该参数影响疾病图的分辨率和计算的速率的可靠性。 方法 内核,带宽的大小,是影响在KDE [在地图上的平滑的程度的关键参数 ]。带宽可以是固定的也可以是可变的(自适应的)。对于固定带宽方法,内核具有固定大小的半径,并且所有内核(圆圈)具有相同的半径。在健康研
区间预测 | Matlab实现GRU-Adaboost-ABKDE的集成门控循环单元自适应带宽核密度估计多变量回归区间预测
区间预测 | Matlab实现GRU-Adaboost-ABKDE的集成门控循环单元自适应带宽核密度估计多变量回归区间预测 目录 区间预测 | Matlab实现GRU-Adaboost-ABKDE的集成门控循环单元自适应带宽核密度估计多变量回归区间预测效果一览基本介绍程序设计参考资料 效果一览 基本介绍 1.Matlab实现GRU-Adaboost-ABKD
区间预测 | Matlab实现CNN-BiLSTM-KDE的卷积双向长短期神经网络结合核密度估计多变量时序区间预测
区间预测 | Matlab实现CNN-BiLSTM-KDE的卷积双向长短期神经网络结合核密度估计多变量时序区间预测 目录 区间预测 | Matlab实现CNN-BiLSTM-KDE的卷积双向长短期神经网络结合核密度估计多变量时序区间预测效果一览基本介绍程序设计参考资料 效果一览 基本介绍 1.CNN-BiLSTM-KDE多变量时间序列区间预测,基
区间预测 | Matlab实现CNN-LSTM-KDE的卷积长短期神经网络结合核密度估计多变量时序区间预测
区间预测 | Matlab实现CNN-LSTM-KDE的卷积长短期神经网络结合核密度估计多变量时序区间预测 目录 区间预测 | Matlab实现CNN-LSTM-KDE的卷积长短期神经网络结合核密度估计多变量时序区间预测效果一览基本介绍程序设计参考资料 效果一览 基本介绍 1.CNN-LSTM-KDE多变量时间序列区间预测,基于卷积长短期记忆神经网
植株计数-密度估计-从高分辨率RGB图像中快速实现高通量植物计数
TasselNetv2+ TasselNetv2+亮点安装准备数据推断训练使用自己的数据集引用 TasselNetv2+ 该存储库包含TasselNetv2+用于植物计数的官方实现,详见论文: TasselNetv2+: A Fast Implementation for High-Throughput Plant Counting from High-Resolution
区间预测 | Matlab实现BP-KDE的BP神经网络结合核密度估计多变量时序区间预测
区间预测 | Matlab实现BP-KDE的BP神经网络结合核密度估计多变量时序区间预测 目录 区间预测 | Matlab实现BP-KDE的BP神经网络结合核密度估计多变量时序区间预测效果一览基本介绍程序设计参考资料 效果一览 基本介绍 1.BP-KDE多变量时间序列区间预测,基于BP神经网络多变量时序区间预测,BP神经网络的核密度估计下置信区间预测
从零开始实现核密度估计(kernel density estimation,KDE)-python实现
问题背景 核密度估计(kernel density estimation)是在概率论中用来估计未知的密度函数,属于非参数检验方法之一,由Rosenblatt (1955)和Emanuel Parzen(1962)提出,又名Parzen窗(Parzen window)。 具体原理推导可参考这篇博客。 此篇博客侧重于根据理论公式,给出python实现。 python工具包推荐 seaborn
核密度估计原理及sparkpython实现
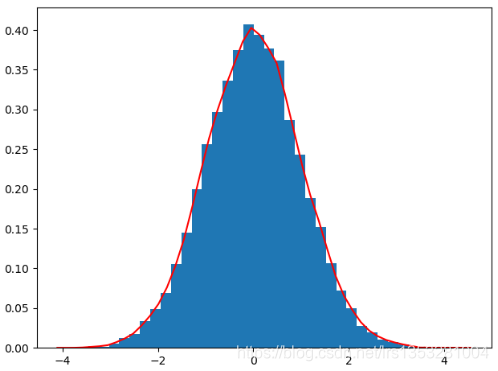
核密度估计属于非参数估计,它主要解决的问题就是在对总体样本的分布未知的情况,如何估计样本的概率分布。 像平时,我们经常也会用直方图来展示样本数据的分布情况,如下图: 但是,直方图有着明显的缺点: 非常不平滑,邻近的数据无法体现它们的差别;不同的bins画出的直方图差别非常大;无法计算概率密度值。 核密度估计 核密度估计就可以很好的解决直方图存在的问题,它的原理其实也很简单:当你需要估计一个
SaCNN人群密度估计测试
现实问题:随着社会的发展,城市人口的扩增,导致城市特定场所人口聚集度越来越大,不安全因素随之扩大。有效地估计特定场所的人口密度以及计算当前场景的人口数量对道道路安全和交通管理来说显得尤为重要。 解决来源(之一):WACV'18 paper - Crowd counting via scale-adaptive convolutional neural network (SaCNN) 文章
功率谱密度估计 - welch方法的实现
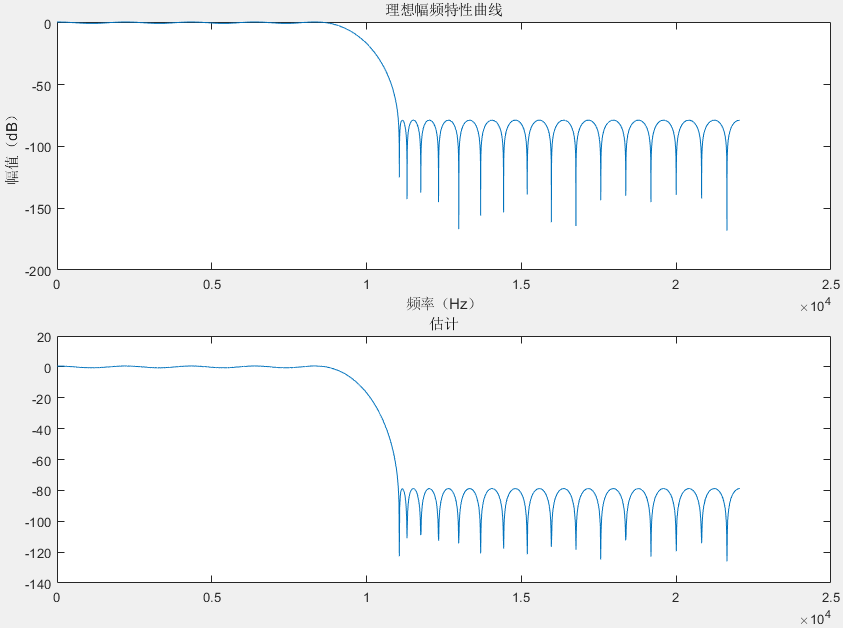
因本人知识欠缺,后续再对下述展开讲述。 clc;clear;close all;fs = 44100;t = 0:1/fs:1-1/fs;x = randn(size(t));load("myfir64.mat");filtercoe = myfir64;y = filter(filtercoe, 1, x);[Hx, w] = freqz(filtercoe, 1, fs);fx
数据分析介绍之三——单变量数据观察之核密度估计
数据分析介绍之三——单变量数据观察之核密度估计 一、核密度估计 上一篇结尾处谈到了直方图的几个缺点,幸运的是,除了这些问题之外,还有经典直方图的替代方案。 称为核密度估计。 内核密度估计(KDEs)是一种比较新的技术。 与直方图和许多其他经典数据分析方法相比,它们几乎要求合理的现代计算机的计算能力有效。 即使是相当适中的数据集,它们也不能用纸和铅笔手工完成。 (有趣的是,计算和图形功能的