“傻瓜”学计量——核密度估计KDE

本文主要是介绍“傻瓜”学计量——核密度估计KDE，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

提纲：

什么是核密度估计，是干什么的

代码

1 前言

参数估计vs非参数估计
参数估计	是样本数据来自一个具有明确概率密度函数的总体。
非参数估计	是样本数据的概率分布未知，这时，为了对样本数据进行建模，需要估计样本数据的概率密度函数。

核密度估计Kernel Density Estimation即是非参数估计的一种方式。即，核密度估计的目的：就是估测所给样本数据的概率密度函数。在论文中的应用就是解读演化趋势。

KDE的数学公式推导请看核密度估计（KDE）原理及实现-CSDN博客

2 核密度估计是什么

用有限的样本推断总体数据的分布，因此，核密度估计的结果即为样本的概率密度函数估计。

1.1 从直方图理解核密度估计图

核密度估计其实是对直方图的一个自然拓展。

第一，我们看密度的时候会先画直方图，用以表示样本数据的分布，帮助分析样本数据的众数、中位数等性质，横轴表示变量的取值区间，纵轴表示在该区间内数据出现的频次与区间的长度的比例。

第二，一个很自然的想法是，如果我们想知道X=x处的密度函数值，可以像直方图一样，选一个x附近的小区间，数一下在这个区间里面的点的个数，除以总个数，应该是一个比较好的估计。用数学语言来描述，如果你还记得导数的定义，密度函数可以写为：

$f(x)=\lim _{h\rightarrow 0}\frac{F\left ( x+h \right )-F\left ( x-h \right )}{2h}$

那么一个很自然的问题来了，h该怎么选取呢？

这也就是非参数估计里面的bias-variance tradeoff：如果h太大，用于计算的点很多，可以减小方差，但是方法本质要求h→0，bias可能会比较大；如果h太小，bais小了，但是用于计算的点太少，方差又很大。

第三，所以理论上存在一个最小化mean square error的一个h。一般我们会把h叫做「窗宽（bandwidth）

此时的概率分布图将会比较光滑，如右：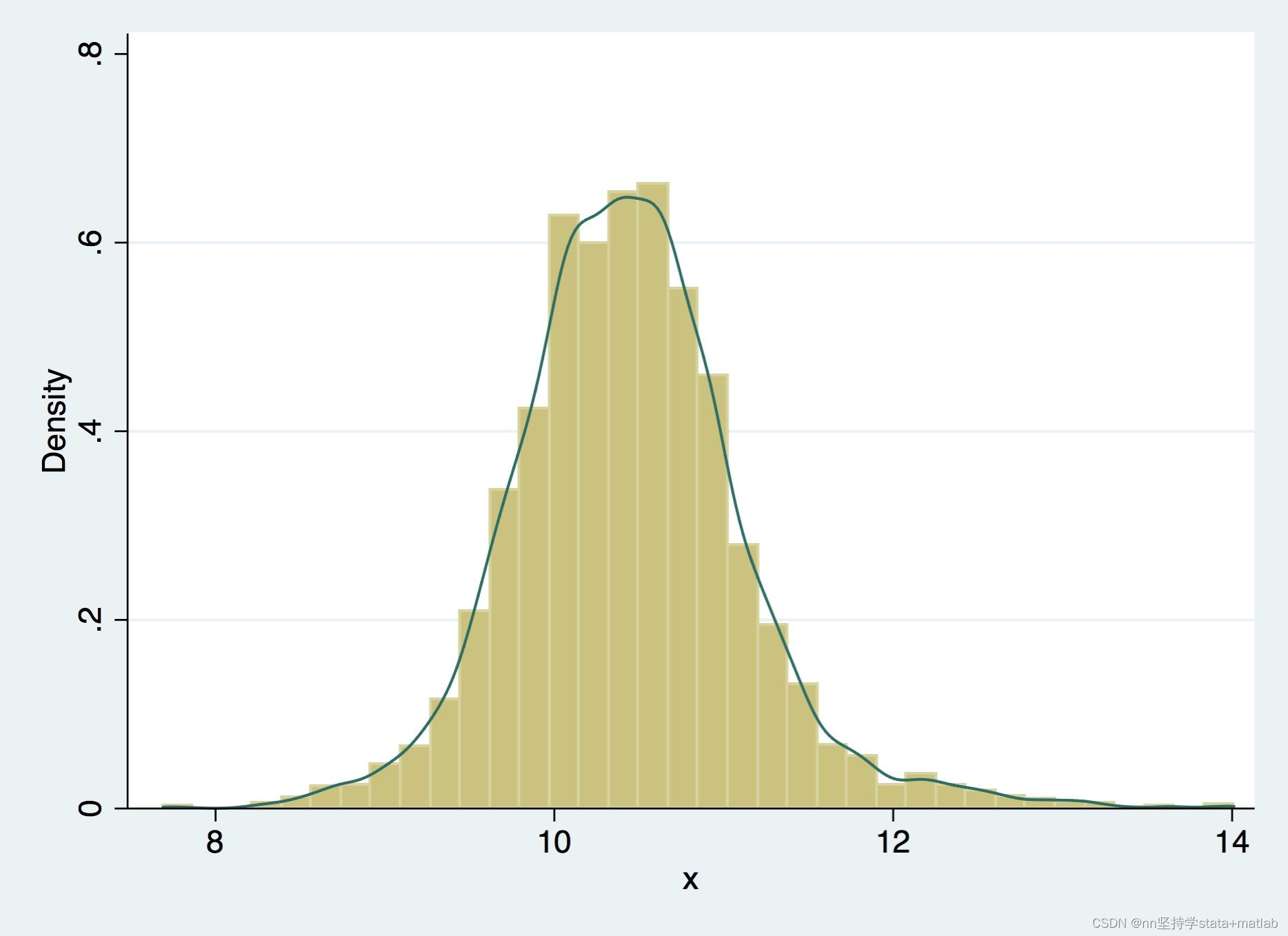

2 核密度估计KDE代码

1	`ssc install kdens`	安装指令
2	twoway kdensity 变量名	画出这个变量的核密度曲线 twoway是一个二维坐标 kdensity是核密度函数图
3	twoway kdensity 变量名 [aw=变量名2]	考虑权重 aw
4	twoway kdensity 变量名1 [aw=变量名2] if 变量名1<=300000，bw(10000)	限制横坐标最大值 300000横坐标最大值300000 bw(10000)是设置带宽10000
5	twoway kdensity 变量名1 [aw=变量名2] if 变量名1<=300000，bw(10000) lp(dash)	lp(dash) 线型是虚线 dash 虚线 solid 实线 longdash 长虚线 longdash_dot 长虚线加点 shortdash 短虚线
6	twoway kdensity 变量名1 [aw=变量名2] if 变量名1<=300000，bw(10000) lp(dash) color(black)	color(black) 线是黑白色
7	twoway kdensity 变量名1 [aw=变量名2] if 变量名1<=300000，bw(10000) lp(dash) color(black) xlabel(0(50000)300000) ylabel(0.0(0.00001)0.00002)	设置横纵坐标 xlabel(0(50000)300000)横坐标从1~300000，间隔50000 ylabel(0.0(0.00001)0.00002)纵坐标是从0-0.00002，间隔0.00001
8	twoway kdensity 变量名1 [aw=变量名2] if 变量名1<=300000，bw(10000) lp(dash) color(black) xlabel(0(50000)300000) ylabel(0.0(0.00001)0.00002) xtitle() ytitle(）	设置横纵坐标名称 xtitle() ytitle(）
9	twoway kdensity 变量名1 [aw=变量名2] if 变量名1<=300000，bw(10000) lp(dash) color(black) xlabel(0(50000)300000) ylabel(0.0(0.00001)0.00002) xtitle() ytitle() graphregion(fcolor(white) lcolor(white))	底色变白，否则默认底色为蓝，打印出来就是灰色的 graphregion(fcolor(white) lcolor(white)) fcolor 底色/背景色 lcolor 外框线颜色
10	twoway kdensity finc_20 [aw=fswt_20] if finc_20 <= 300000, bw(10000) lp(solid) color(black) \|\| kdensity finc_18 [aw=fswt_18] if finc_18<= 300000, bw(10000) 1p(longdash) color(black) \|\| kdensity finc_16 [aw=fswt_16] if finc_16 <= 300000, bw(10000) 1p(longdash_dot) color(black) \|\| kdensity finc_14 [aw=fswt_14] if finc_14 <= 300000, bw(10000) 1p(dash) color(black) \|\| kdensity finc_12 [aw=fswt_12] if finc_12 <= 300000, bw(10000) lp(shortdash) color(black) \|\| kdensity finc_10 [aw=fswt_10] if finc_10 <= 300000, bw(10000) lp(dash_dot) color(black) xlabel(0(50000)300000)ylabel(0.0(0.00001)0.00002)xtitle(家庭收入(元))ytitle(核密度)graphregion(fcolor(white) lcolor(white))	同一个图中画多条核密度曲线 \|\| 隔开
11	twoway kdensity finc_20 [aw=fswt_20] if finc_20 <= 300000, bw(10000) 1p(solid) color(black) \|\| kdensity finc_18 [aw=fswt_18] if finc_18<= 300000, bw(10000) lp(longdash) color(black) \|\| kdensity finc_16 [aw=fswt_16] if finc_16 <= 300000, bw(10000) lp(longdash_dot) color(black) \|\| kdensity finc_14 [aw=fswt_14] if finc_14 <= 300000, bw(10000) lp(dash) color(black) \|\| kdensity finc_12 [aw=fswt_12] if finc_12 <= 300000, bw(10000) 1p(shortdash) color(black) \|\| kdensity finc_10 [aw=fswt_10] if finc_10 <= 300000, bw(10000) lp(dash_dot) color(black) xlabel(0(50000)300000) ylabel(0.0(0.00001)0.00002) legend(label(1 "202@)label(2 "2018")label(3 "2016")label(4 "2014") label(5"2012")label(6"2010"))xtitle(家庭收入(元))ytitle(核密度)graphregion(fcolor(white)lcolor(white))	设置图例 legend
12	twoway kdensity finc_20 [aw=fswt_20] if finc_20 <= 300000, bw(10000) 1p(solid) color(black) \|\| kdensity finc_18 [aw=fswt_18] if finc_18<= 300000, bw(10000) lp(longdash) color(black) \|\| kdensity finc_16 [aw=fswt_16] if finc_16 <= 300000, bw(10000) lp(longdash_dot) color(black) \|\| kdensity finc_14 [aw=fswt_14] if finc_14 <= 300000, bw(10000) 1p(dash) color(black) \| \| kdensity finc_12 [aw=fswt_12] if finc_12 <= 300000, bw(10000) lp(shortdash) color(black) \|\| kdensity finc_10 [aw=fswt_10] if finc_10 <= 300000, bw(10000) lp(dash_dot) color(black) xlabel(0(50000)300000) ylabel(0.0(0.00001)0.00002) legend(label(1 "2020")label(2 "2018")label(3 "2016")label(4 "2014") label(5"2012")1abel(6"2010")row(2))xtitle(家庭收入(元))ytitle(核密度)graphregion(fcolor(white)lcolor(white))	设置图例的行数 row(2)行数为2
13	graph save 保存路径，replace	保存图片