本文主要是介绍从零开始实现核密度估计(kernel density estimation,KDE)-python实现,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
问题背景
核密度估计(kernel density estimation)是在概率论中用来估计未知的密度函数,属于非参数检验方法之一,由Rosenblatt (1955)和Emanuel Parzen(1962)提出,又名Parzen窗(Parzen window)。
具体原理推导可参考这篇博客。
此篇博客侧重于根据理论公式,给出python实现。
python工具包推荐
seaborn,pandas,scikit-learn中均提供了kde计算及绘图函数,可直接查阅/调用。
理论基础
核密度估计的核心公式如下:

其中,h为带宽(band_width),K(.)为核函数,本文选取高斯核。
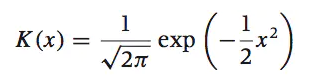
带宽h是一个超参数,h越小,邻域中参与拟合的点越少。h有多种选取方式,
本文参考网上资料采用如下公式:
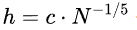
其中c=1.05*数据序列标准差
python实现
根据以上背景,给出kde 计算函数如下:
def get_kde(x,data_array,bandwidth=0.1):def gauss(x):import mathreturn (1/math.sqrt(2*math.pi))*math.exp(-0.5*(x**2))N=len(data_array)res=0if len(data_array)==0:return 0for i in range(len(data_array)):res += gauss((x-data_array[i])/bandwidth)res /= (N*bandwidth)return res
其中x为待进行估计的数据点,data_array为给定的数据序列(list)。
KDE计算及绘制demo
测试环境
python 3.7
matplotlib 3.0.3
numpy 1.16.2
demo
def get_kde(x,data_array,bandwidth=0.1):def gauss(x):import mathreturn (1/math.sqrt(2*math.pi))*math.exp(-0.5*(x**2))N=len(data_array)res=0if len(data_array)==0:return 0for i in range(len(data_array)):res += gauss((x-data_array[i])/bandwidth)res /= (N*bandwidth)return res
import numpy as np
input_array=np.random.randn(20000).tolist()
bandwidth=1.05*np.std(input_array)*(len(input_array)**(-1/5))
x_array=np.linspace(min(input_array),max(input_array),50)
y_array=[get_kde(x_array[i],input_array,bandwidth) for i in range(x_array.shape[0])]
import matplotlib.pyplot as plt
plt.figure(1)
plt.hist(input_array,bins=40,density=True)
plt.plot(x_array.tolist(),y_array,color=‘red’,linestyle=’-’)
plt.show()
运行结果
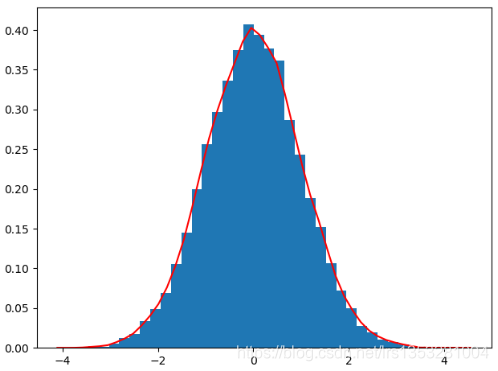
结果说明:
图中横轴为数据分布取值,纵轴为概率密度,其中直方图的高度 h = 频数/(总数*每个bin的宽度) ,直方图总面积是1,KDE曲线下总面积也是1。
参考资料
- 维基百科-Kernel density estimation
- 知乎相关回答
- 核密度估计-CSDN博客
这篇关于从零开始实现核密度估计(kernel density estimation,KDE)-python实现的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







